§ 2. Расчет времени слива нефтепродуктов из железнодорожных цистерн

Задача об определении времени опорожнения цистерн вследствие непрерывного изменения напора, а следовательно, и скоростей во времени является примером неустановившегося движения жидкости. Поэтому при решении этой

задачи следует воспользоваться известным приемом, по которому полное время истечения разделяют на бесконечно малые промежутки времени, в течение каждого из которых напор считают постоянным, а движение жидкости установившимся. Это позволяет использовать определенные зависимости установившегося движения.

В общем случае слив из цистерн может происходить через сливной трубопровод и при избыточном давлении в цистерне. При этом режим истечения может быть турбулентный в начале слива, ламинарный — в конце. В частных случаях возможно истечение только при одном режиме (рис. 2.6).

Рис. 2.6. К расчету времени слива нефтепродуктов из железобетонных цистерн.

Рассмотрим решение этой задачи в целом. Положим, что за время d уровень нефтепродукта в цистерне понизился на dz. Слитый из цистерны объем составит qd. Из условия неразрывности потока

(2.27)

где q — расход нефтепродуктов в м³/с; f — площадь поперечного сечения потока нефтепродукта, вытекающего через сливной патрубок, в м²; w— скорость истечения нефтепродукта из цистерны в м/с; F — площадь свободной поверхности нефтепродукта в цистерне в м².

Значение F, как функцию переменной ординаты z, можно получить из рассмотрения треугольника АОВ (см. рис. 2.6):

или

где L — длина котла цистерны в м.

Для определения w воспользуемся уравнением Бернулли

где _к — коэффициент местного сопротивления сливного клапана; l_np, d — приведенные длина и диаметр сливного трубопровода в м; — плотность сливаемого нефтепродукта в кг/м³.

Остальные обозначения даны на рис. 2.6.

Решая уравнение Бернулли относительно скорости, получаем

(2.28)

где — коэффициент расхода системы.

Подставив значения F и w в уравнение (2.27) и разделив переменные, получим

(2.29)

Дифференциальное уравнение (2.29) представляет собой общий вид функциональной зависимости времени истечения от переменных величин z и _с. Для решения этого уравнения необходимо знать закономерность изменения _с. в процессе истечения. Но такая закономерность может быть установлена только экспериментально для конкретных условий слива. По этой причине рассмотрим частные случаи слива, для которых известен характер изменения _с.

Первый случай. Слив через короткий патрубок

Дано: h₀ = 0; р_и = 0, р₁ = р₂ и равно атмосферному давлению р_а. Тогда уравнение (2.29) упростится и примет вид

(2.29а)

где ₀ — коэффициент расхода сливного клапана с патрубком.

Рис. 2.7. Экспериментальная зависимость коэффициента расхода универсального сливного прибора железнодорожной цистерны от Re .

Натурные экспериментальные исследования по сливу нефтепродуктов из цистерн объемом 50 и 60 м³, оборудованных универсальным сливным прибором (d = 0,2 м), позволили получить зависимость ₀ = f (Re_т).

Из кривой ₀ = f (Re_т), приведенной на рис. 2.7, следует, что коэффициент расхода сливного прибора резко меняется при малых текущих Re_т = достигая постоянного значения при

Следовательно, для практических расчетов =const только при Re_т.

Таким образом, уравнение (2.29а) правомерно интегрировать при ₀ = const только в пределах от D до z_кр, соответствующей границе перехода турбулентного режима в ламинарный. Для определения же полного времени слива необходимо весь процесс истечения разделить на две части: на время истечения при турбулентном режиме (_т) и ламинарном (_л). Тогда =_т + _л. Но, как отмечалось выше, const и для определения _л необходимо в уравнение (2.29а) ввести =f (Re_т). Это обстоятельство значительно усложняет решение и затрудняет практическое пользование полученными формулами вследствие их громоздкости. Поэтому для упрощения расчетов времени слива полученные экспериментальные значения ₀ в процессе слива каждой цистерны были усреднены во времени и таким образом получены приведенные значения _о для различных вязкостей. Опыты проводились в интервале изменения кинематической вязкости от 1 до 650 см²/с Полученная кривая _о = f (Re_т) затем была апроксимирована зависимостью

(2.30)

где v — кинематическая вязкость в см²/с.

Полагая, что вязкость нефтепродукта за время слива постоянна, и зная v при температуре слива, можно по (2.30) найти _о, положив его постоянным при интегрировании уравнения (2.29а) в пределах от D до 0:

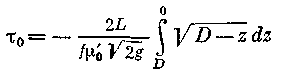
или

(2.31)