Насосные гпрс

Перемещение жиженных газов с помощью только насосов является довольно интересным с точки зрения надежности, удобства, простоты, малых энергетических затрат и капитальных вложений. Однако для этого необходимо ре­шить вопрос о создании специальных самовсасывающих насосов или создать условия, при которых насосы всегда находились под действием гидростати­ческого напора столба жидкости. Кроме того, отечественная промышленность выпускает железнодорожные цистерны только с верхним сливом сжиженного газа, что затрудняет применение чисто насосной схемы слива.

Насосно-инжекторные гпрс

Схема станций сжиженного газа, в которой используется насосно-инжекторный способ перемещения продукта, представлена на рис. 11.4.

Рис. 11.4. Перемещение сжиженного газа насосно-инжекторным методом.

1 —способ отсоса инжектором паров из сепаратора и подъема за счет этого жидкости на высоту; 2 — способ создания избыточного давления во всасывающем патрубке насоса; 3 — инжектор; 4 — сепаратор; 5 — насос; 6 — линия рециркуляции; 7 — запорный вентиль; 8 — вентиль для залива жидкости.

Инжектор работает с помощью части жидкости (до 40—60%), подаваемой насосом 5.

В схему включен напорный сосуд 4, который служит для постоянного залива жидкостью всасывающего патрубка насоса и сепарации паровой и жидкостной фаз после инжектора. Данная схема имеет замкнутое кольцо циркуляции сжиженного газа по пути: резервуар — инжектор — напорный сосуд — насос — наполнительная рампа (другой резервуар, куда перекачивается жидкость) — резервуар. В этой схеме насос работает в области относительно постоянного и потому устойчивого режима, независимо от интенсивности разбора сжиженного газа на рампе.

Преимущество метода перекачки с помощью насосов — меньший расход энергии при перекачке. Недостатки метода: необходимость наличия источника энергии; сложность схемы обвязки насосов и пуска их в разные периоды года; ненадежность работы (срывы работы насосов); большие эксплуатационные затраты по ремонту для существующих насосов; большие потери газа на включение насосов и ликвидацию срыва работы их (продувка насосов с выпуском паров); необходимость прекращать наполнение баллонов при заправке автоцистерн или иметь дополнительные насосы; невозможность полностью удалить жидкость и пары из железнодорожных цистерн при сливе; большой расход энергии (непрерывная работа в течение всего рабочего времени станции); низкий к. п. д. насосов; непригодность насосов, используемых для наполнения баллонов, для слива цистерн (небольшая производительность).

§ 3. Процессы слива — налива сжиженных газов

Рассмотрим истечение сжиженного углеводородного газа из горизонтально-цилиндрического резервуара 1 диаметром D₁ и длиной L₁ (рис. 11.5) в такой же резервуар диаметром D₂ и длиной L₂ через сливной трубопровод площадью поперечного сечения f и приведенной длиной l_пр. В резервуаре создано давление р_см при закачке в его паровое пространство инертного газа. По мере освобождения резервуара давление падает. Предположим, что парциальное давление паров сливаемого продукта остается на прежнем уровне. Тогда уменьшение давления смеси паров будет происходить только за счет уменьшения парциального давления инертного газа.

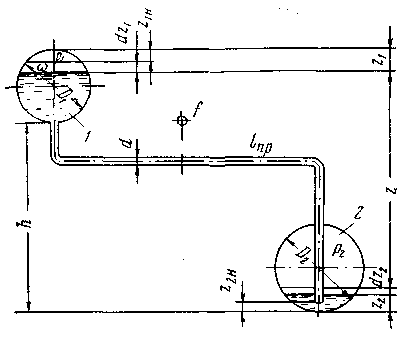
Рис. 11.5. Схема сжиженного газа (углеводородного) из резервуара.

В резервуаре 2 давление р₂ остается постоянным (принимается, что резервуарный парк имеет газоуравнительную систему).

Предположим, что ось z направлена в сторону движения нефтепродукта. За время dτ уровень в резервуаре 1 понизится на dz₁ и из него вытечет некоторое количество нефтепродукта:

(11.1)

где  — коэффициент расхода; ω — площадь зеркала продукта в освобождаемом резервуаре:

(11.2)

Активный напор z получаем из схемы слива (рис. 11.5):

(11.3)

где р_и — парциальное давление инертного газа в резервуаре 1; р_п — парциальное давление паров нефтепродукта; γ_ж — удельный вес жидкости (γ_ж =ρ_жg)

Исходя из равенства объемов слитой из резервуара 1 и поступившей в резервуар 2 жидкости, выразим z₂ через z₁; заменим в уравнении (11.3) р_п, выразив его из уравнения состояния, и, подставив значения (11.2) и (11.3) в формулу (11.1), решим его относительно dτ :

(11.4)

где

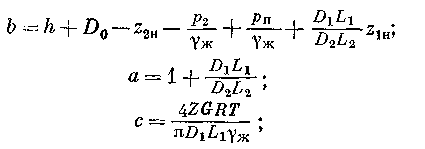
z_1н — недоливаемый уровень нефтепродукта в освобождаемом резервуаре; z_2h — начальный уровень нефтепродукта в наполняемом резервуаре; Z — коэффициент сжимаемости; G — вес инертного газа; R — газовая постоянная.

Интегрирование уравнения (11.4) приводит к эллиптическим интегралам первого и второго рода.

После интегрирования и соответствующих преобразований имеем:

где F и Е — эллиптические интегралы первого и второго рода;

k — модуль эллиптических интегралов

φ — амплитуда эллиптических интегралов

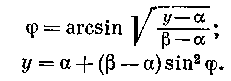
При полном освобождении резервуара 1 и z_lн = 0 формула (11.5) примет вид

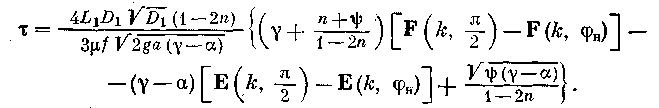(11.5а)

В формулах (11.5) и (11.5а) индексы «в» и «н» означают соответственно «верхний» и «нижний», а ф_н определяется из выражения

Если слив сжиженного газа идет при р_см = const, то φ = 0; α = 0; γ = п. Тогда при направлении оси z вверх формула (11.5) переходит в формулу М. С. Илембитова:

(11.5б)

где

Пример 11.1. Определить время истечения н-Бутана из горизонтально-цилиндрического резервуара в такой же резервуар, имеющий D₁ = 2,6 м; L₁ = 10,1 м; Т₁ = Т₂ = 5° С; р_см = 7 кгс/см²; р₂ = 1,2 кгс/см²; γ_ж = = 595 кг/м³; а = 2; b = 3,24; f= 0,00785 м²;  = 0,18.

Вытеснение производится метаном: G = 53 кг; R = 52,9 (кгс·м)/(кг · К); Z = 0,98; α = 1,388; β = 1; γ = 2,12; п = 0,625; φ= 2,785; φ_н = 49°15'; φ_в =

По таблицам функций F (k, .) = 2,034; Е (k, ) = 1,261; F (k, ) = 0,93; Е(k,φ_н) = 0,7905.

Решение. По формуле (11.5а) τ = 33,6 мин.

Расчет конструктивных примеров позволяет выявить зависимость времени освобождения резервуара от начального перепада давлений.

Анализируя эту зависимость, можно сделать вывод, что перепад давления выше 4—5 кгс/см² существенного сокращения времени слива не дает. Поэтому следует принимать перепад равным 2—4 кгс/см².

Рассмотрим компрессорный способ слива сжиженного газа из резервуара компрессор нагнетает пары сливаемого газа в паровое пространство емкости до определенного давления, одновременно происходит слив жидкости.

Для решения поставленной задачи необходимо рассмотреть уравнение теплового баланса системы пар — жидкость — металл емкости и уравнение материального баланса.

Уравнение теплового баланса системы связывает тепло, подведенное к системе извне, с изменением теплосодержания каждого элемента системы в отдельности.

Уравнение материального баланса устанавливает связь между количеством поданного в емкость пара, количеством слитой за время работы компрессора жидкости с изменением массы пара и жидкости в емкости.

При совместном решении уравнений теплового и материального баланса принято:

1. вследствие постоянства объема емкости скорости изменения объемов жидкости и пара равны;

2. скорость изменения температуры металла равна скорости изменения температуры пара;

3) скорости изменения физических параметров жидкости и пара при помощи частных производных связаны со скоростью изменения давления в емкости.

В результате имеем:

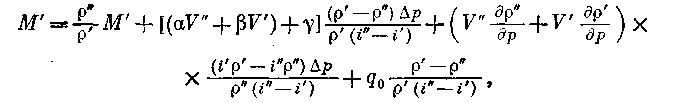(11.6)

где

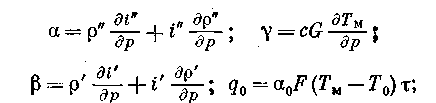
М" и М' — масса поданного пара и слитой жидкости; Т_м и Т_o — температуры металла и окружающей среды; G и с — вес и теплоемкость металла емкости; F — поверхность резервуара; τ — время нагнетания.

Значения плотностей, объемов и энтальпий жидкости и пара являются первоначальными. Значения коэффициентов и в интервале температур от 0 до 30° С могут быть приняты постоянными. Они легко определяются из соответствующих таблиц и диаграмм. Температура металла с достаточной степенью точности может быть принята равной среднеарифметической температуре пара за время нагнетания.

В формуле (11.6) первый член равенства выражает расход пара на заполнение объема, ранее занятого жидкостью, второй и третий — на изменение теплосодержания жидкости и пара, четвертый — на теплоотдачу в окружающую среду. Если процесс слива производится таким образом, что прогреванию подвергается не вся масса жидкости, а только ее верхний незначительный слой,

то, приняв = 0 и = 0, получим

(11.7)

Пример 11.2. Определить расход паров на слив пропана из автоцистерны АЦЖГ-12-200В. Степень заполнения цистерны f = 0,83; G = 5000 кг; с = 0,105 ккал/(кг·°С), температура t' = 0° С; t₀ = -1° С; V" = 2,18 м³; V' = 12 м³; р_н = 4,9 кгс/см²; р_к = 8,5 кгс/см²; α = 260·10^-4 ккал (кгс·м); β= 1503 · 10^-4 ккал (кгс·м); γ = 2260 · 10^-4 (ккал·м²)/кгс; q₀ = 1140 ккал.

Решение.

По формуле (11.6) М" = 961,15 кг; по формуле (11.7) М" = 156,25 кг.

При прогреве всей массы жидкости расход пара увеличивается прямо пропорционально отношению начального объема жидкости к начальному объему пара.

При компрессорном способе перемещения сжиженных углеводородных газов в паровое пространство освобождаемой емкости нагнетают пары этого же газа, давление которых доводят до необходимой для перемещения величины. По достижении заданного давления подача пара прекращается. Слив производится при уменьшающемся давлении в паровом пространстве. Причем нижний предел давления не должен быть меньше заранее заданной определенной величины. Вопрос о том, какое количество жидкости может быть слито за время падения давления от максимальной до минимальной величины, имеет большое практическое значение. С одной стороны, это дает возможность определить удельный расход паров для перемещения жидкости, т. е. отношение массы поданного пара к массе слитой жидкости. С другой стороны, при заданной производительности сливо-наливных операций решение этого вопроса определит интенсивность работы компрессорной установки.

Для решения поставленной задачи рассмотрены уравнения теплового баланса системы нар — жидкость — металл емкости и уравнение материального баланса емкости.

Уравнение теплового баланса системы связывает тепло, подведенное к системе извне, с изменением теплосодержания каждого элемента системы в отдельности. Причем тепло внутреннего теплообмена принято равным нулю.

Уравнение материального баланса устанавливает связь за время падения давления от максимальной величины до минимальной с изменением массы пара, и жидкости в емкости.

В результате имеем:

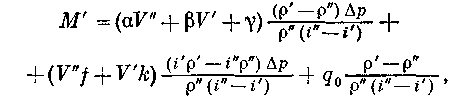(11.8)

где

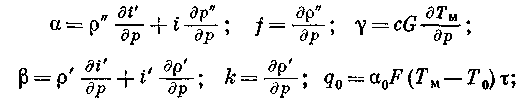
М' — количество слитой жидкости; Т_м и Т₀ — температуры металла емкости и окружающей среды; G и c — вес металла емкости и его удельная теплоемкость; F — поверхность резервуара; τ — время слива.

Значения плотностей, объемов и энтальпий пара и жидкости равны значе­ниям в конце нагнетания и в начале слива.

Значения коэффициентов и в интервале температур от 0 до 30° С могут быть приняты постоянными. Они легко определяются из соответствующих таблиц и диаграмм. Температуру металла с достаточной степенью точности можно принять равной среднеарифметической температуре пара за время слива. Если подача пара в паровое пространство резервуара производилась таким образом, что прогревался только ее верхний незначительный слой, то, приняв = 0 и = 0, получим:

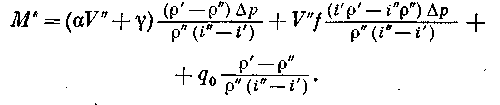(11.9)

Пример 11.3. Определить количество слитого сжиженного пропана из автоцистерны АЦЖГ-12-200В. Степень наполнения φ = 0,57; V" = 6 м³; V' = 8 м³; G = 5000 кг; с = 0,105 ккал(кг ·°С); t' = 0° С; t₀ = 1° С; р_н = = 8,5 кгс/см²; р_к = 5,5 кгс/см²; α = 281,3·10 ^-4 ккал/(кгс·м); γ = 2360 ·10^-4 (ккал·м²)/кгс; q₀ = 2500 ккал;

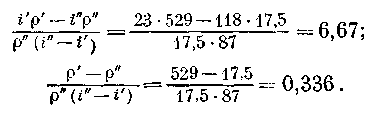
Подставив цифровые значения величин в формулу (11.8), получим М' = 4643 кг.