metod_uk_4sem / Волновая оптика (41-48) PDF / Мет. 41

Федеральное агентство по образованию РФ Ухтинский государственный технический университет

41

Изучение интерференции с помощью бипризмы Френеля

Методические указания к лабораторной работе для студентов всех специальностей дневной и заочной формы обучения

Ухта

2007

ИЗУЧЕНИЕ ИНТЕРФЕРЕНЦИИС ПОМОЩЬЮ

БИПРИЗМЫ ФРЕНЕЛЯ

Цель работы: определение угловой ширины зоны интерференции и длин волн, пропускаемых различными светофильтрами.

ТЕОРИЯ РАБОТЫ

Интерференция света относится к тем оптическим явлениям, в которых проявляется волновая природа света.

Свет, с точки зрения электромагнитной теории, представляет собой поп е- речные волны, распространяющиеся в вакууме со скоростью с = 3·10 8 м/с.

В световой волне совершают быстрые непрерывные колебания векторы н а- пряженности электрического E и магнитного H полей. Их колебания взаимосвязаны и происходят в направлениях, пе рпендикулярных лучу, причем так, что E и H взаимно перпендикулярны (см.рис.1). Как показывает опыт, действие света на

где E и EM – мгновенное и амплитудное (максимальное) значения светового вектора, – частота колебаний. Фаза волны определ яется выражением

3

2 ( t r ) .

Свет, имеющий определенную частоту (или длин у волны), называется монохроматическим. Монохроматические волны различных частот вызывают у ч е- ловека световые ощущения. Например, свет с частотой ν = 4·1015 Гц воспринимается как красный, с частотой ν = 6·1015 Гц - как зеленый. Белый свет представляет собой совокупность различных монохроматических волн.

Интерференцией волн называется явление усиления колебаний в одних точках пространства и ослабления колебаний в других точках в результате нал о- жения двух или нескольких волн, приходящих в эти точки.

Поскольку свет представляет собой электромагнитные волны, для него должна наблюдаться интерференция света.

Для наблюдения устойчивой во времени интерференционной картины нео б- ходимы условия когерентности (согласованности) волн.

Источники, излучающие волны одинаковой частоты с постоянной разностью фаз и совпадающими плоскостями колебаний векторов E , называются когерентными. Волны, излучаемые такими источниками, также являются ког е- рентными. В результате наложения когерентных световых волн наблюдается я в- ление интерференции света. Оно проявляется в том, что в одних местах пр о- странства происходит усиление интенсивности света (наблюдается максимум), в других - ослабление интенсивности (минимум).

Как следует из теории электромагнитных волн, интенсивность света I пр о- порциональна квадрату амплитуды светового вектора:

I Em2 .

Из теории сложения гармонических колебаний одного направления и одной частоты известно, что квадрат амплитуды результир ующей волны

где Em1 и Em2 – амплитуды складываемых колебаний;

– их разность фаз.

При этом становится возможным уменьшение амплитуды результирующих кол е- баний до нуля.

Пусть две когерентные волны от источников S1 и S2 проходят разные пути r1 и r2 и интерферируют в точке Р (рис.2). Амплитуды обоих колебаний примем

4

одинаковыми и обозначим через Em . Тогда мгновенные значения величин, скл а- дываемых в точке наложения равны:

плитуда складываемых колебаний, согласно (1) максимальна (E p 2Em ) . В этом

случае в точке наложения волн образуется максимальная интенсивность (осв е- щенность) или, говорят, наблюдается интерференционный максимум .

E p 0 .

В этом случае наблюдается минимальная интенсивность – минимум.

Так как разность фаз (при условии, что начальные фазы источников S1 и S2 одинаковы), может возникнуть только из -за разности путей r1 и r2 , проходимых лучами, условия наблюдения максимумов и минимумов формули руются обычно через разность хода r1 r2 .

Из вышесказанного следует, максимальное усиление интенсивности св е-

та (максимум) наступает в тех точках пространства, для которых ра з- ность хода слагаемых волн равна целому числу волн или четному чис лу полуволн, т.е.

где (k = 0, 1,2....).

Ослабление интенсивности света (минимум) наблюдается в тех то ч- ках пространства, для которых разность хода слагаемых волн равна нече т- ному числу полуволн, т.е.

5

S1

S1

Рис.2 иллюстрирует результат наложения волн для случая усиления инте н- сивности света (рис.2а) и ослабления (рис.2б).

Одним из основных условий наблюдения ин терференции света является когерентность.

Независимые источники света не могут быть когерентными, ибо в каждом из них свет испускается множеством атомов, излучающих несогласованно. Ра з- ность фаз колебаний, испускаемых совокупностью атомов таких источников, быстро и беспорядочно меняется во времени.

Однако, можно осуществить различные схемы, в которых искусственно со з- даются когерентные пучки путем расчленения первичного пучка на два и посл е- дующего соединения их в определенной области пространства. Одна из так их схем осуществляется с помощью бипризмы Френеля.

6

Бипризма Френеля состоит из двух призм с малыми преломляющими у г- лами (порядка 30 минут) имеющих одну общую грань (рис.3).

тупого угла бипризмы. Мнимые когерентные источники C1 и C2 возникают в результате преломления лучей в бипризме.

Чтобы понять ход лучей в бипризме, рассмотрим преломление лучей в о д- ной из половинок бипризмы (рис.4).

Обозначим через угол между прошедшим через призму лучом и пада ю- щим на нее. Пользуясь законами геометрической оптики можно показать, что в случае, когда преломляющий угол призмы очень мал и углы падения лучей на грань призмы не очень велики, все лучи отклоняются призмой практически на одинаковый угол

(n 1) , где n - показатель преломления призмы.

Угол падения лучей на призму невелик, поэтому все лучи (лучи 1,2,3, на рис.4) отклоняются призмой на одинаковый угол. На пересечении продолжений прошедших сквозь призму лучей лежит мнимый источник C1 .

7

Любой луч внутри падающего на призму пучка преломляется так, что будет

Если на пути прошедших сквозь бипризму лучей п оставить экран Э, то в области перекрытия пучков, идущих от каждой половины бипризмы, можно н а- блюдать интерференционную картину, т.к. в каждую точку экрана Э в зоне пер е- крытия пучков приходят два когерентных луча – от мнимого источника C1 и мнимого источника C2 . Угловая ширина зоны интерференции зависит только от свойств бипризмы

2 2(n 1) .

Картина интерференции представляет систему чередующихся светлых и темных полос, параллельных щели С .

Синусоидальная кривая на рис.3 описывает распределение интенсивности вдоль экрана в области интерференции. Положение интерференционных макс и- мумов легко определить, воспользовавшись схемой рис.5.

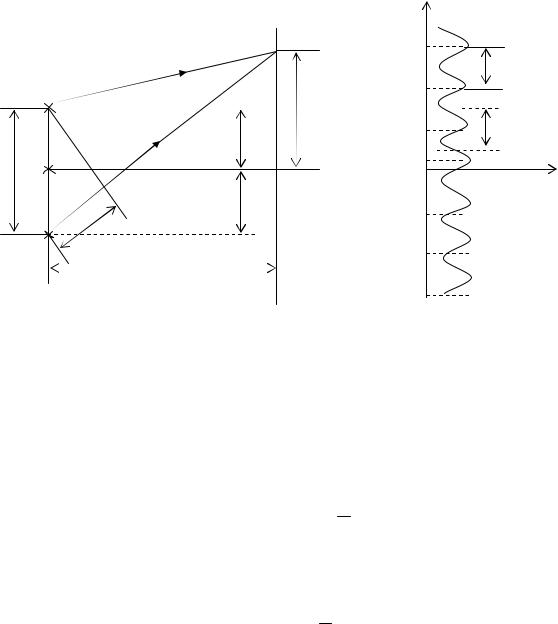
Найдем разность хода лучей для произвольной точки М, находящейся на расстоянии X от центральной линии экрана. Экран располагается на расстоянии L от источника C . Расстояние L много больше расстояния между мнимыми источниками C1 и C2 .

Из рис.5 видно, что

8

r12 r22 (r1 r2 ) (r`1 r2 ) 2Xh .

Из условия L h следует, что (r1 r2 ) 2L . Обозначив искомую разность хода (r1 r2 ) имеем:

2Xh X h . 2L L

Подстановка этого значения в условие (2) дает расстояние X K между центральной линией экрана и положением максимума K-го порядка

X k k L . h

Расстояния между двумя соседними макс имумами

Такой же результат получится, если найти расстояния между соседними минимумами. Расстояние между соседними максимумами (или минимумами) назовем шириной интерференционной полосы .

Ее значение равно

9

Справа на рис.5 показано распределение интенсивности вдоль экрана в м о- нохроматическом свете в зависимости от разности хода лучей, пришедших в данную точку экрана Э.

Предыдущие выводы делались в предположении, что длина волны , излучаемая источником строго монохроматична. В действительности, каждый исто ч- ник излучает набор монохроматических волн от до , где – ширина спектрального интервала.

Рассмотрим, как влияет несоблюдение монохроматичности на интерфере н- ционную картину. Немонохроматичность приводит к постепенному размытию полос по мере удаления от центрального максимума. Дейс твительно, интерференционная картина представляет собой результат наложения интерференционных полос, соответствующих различным длинам волн от до .

Максимум нулевого порядка является общим для всех длин волн. П о мере возрастания максимумы будут раздвигаться, т.к. ширина интерференционной полосы пропорциональна , и с увеличением порядка интерференции максимумы различных длин волн будут налагаться друг на друга.

Интерференционная картина будет размываться по мере удаления от це н- трального максимума и при наложении максимума (к+1) -го порядка для длины волны на максимум k-го порядка для длины волны исчезнет.

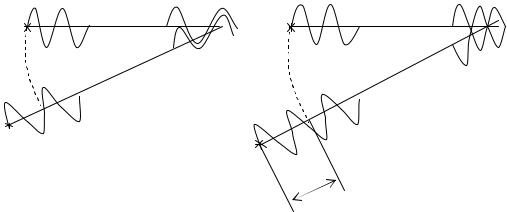
Вышесказанное можно пояснить рисунком 6. Сплошная кривая (рис.6) п о- казывает распределение интенсивности для длины волны вдоль экрана, причем A – максимум К-го порядка, G – максимум (К+1)-го порядка; В, С, Д... – максимумы К-го порядка для длин волн в интервале от , т.е. весь провал между максимумами К-го и (К+1)-го порядков для будет заполнен максимумами к -го порядка промежуточных длин волн данного спектрально го интервала.

10