
glava8
.pdf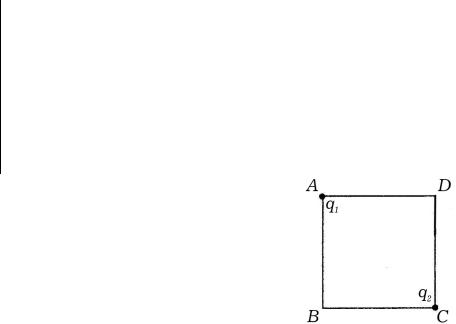
Задача 1. В вершинах А и С квадрата ABCD со стороной a =10 см находят-
ся разноименные заряды q1 = −8 мкКл и q2 = 6 мкКл. Найти потенциал электри-
ческого поля в точке D.
Дано: |
СИ |
a =10 см |
0,1 м |
q1 = −8 нКл |
–8 ×10–9 Кл |
q2 = 6 нКл |
6×10–9 Кл |
|
|
ϕ = ? |
|
|
|
Решение
По принципу суперпозиции электрических по-
лей потенциал поля системы двух точечных зарядов равен алгебраической сумме потенциалов полей этих зарядов
ϕ = ϕ1 +ϕ2 ,
где j1 – |
потенциал электрического поля в точке D, |
|||
создаваемого зарядом q1 , который равен |
||||
j = |
1 |
|
q1 |
; |
4pe0 |
|
|||
1 |
|
a |
||
|
|
|
|
|
j2 – потенциал поля, создаваемого зарядом q2 , который определяется равенством
j2 |
= |
1 |
|
q2 |
. |
|
|
||||
|
4pe0 |
|
a |
||
С учетом этих двух равенств потенциал электрического поля системы двух то-
чечных зарядов в точке D определяется формулой
j = |
1 |
|
q1 |
+ |
1 |
|
q2 |
= |
q1 + q2 |
. |
|
|
|
|
|
||||||
4pe0 a 4pe0 a 4pe0a |
||||||||||
В полученное равенство подставим числовые значения
j = |
|
(-8 ×10−9 Кл + 6 ×10−9 Кл) |
= 180 |
В. |
|
|
×3,14 ×8,85×10−12 |
Ф/м×0,1 м |
|||
4 |
|
|
|||

Задача 2. Протон, пройдя в плоском конденсаторе от одной пластины до другой, приобретает скорость v = 105 м/с. Найдите разность потенциалов между пластинами.
Дано:
v = 105 м/с
m = 1,67 ×10 −27 кг q = 1, 6 ×10 − 19 Кл
ϕ1 −ϕ2 = ?
Решение
Работа электрического поля по перемещению про-
тона между пластинами конденсатора равна
A = q(ϕ1 −ϕ2 ) .
Работа также равна изменению кинетической энер-
гии
A = mv2 . 2
Здесь мы учли, что начальная скорость протона была равна нулю.
Приравняем правые части этих выражений
q(j1 - j2 ) = mv2
2
и выразим разность потенциалов
j1 - j2 = mv2 . 2q
В полученное равенство подставим числовые значения
|
|
|
1,67 ×10−27 |
кг×(105 м/с)2 |
|||
j - j |
2 |
= |
|
|
|
|
= 52 В. |
|
|
|
|
||||
1 |
|
2 |
×1,6 |
×10−19 Кл |
|||
|
|
|
|||||
Задача 3. Пылинка массой m = 0,05 г и с зарядом q =100 нКл перемещает-
ся в электрическом поле из точки А, с потенциалом 6000 В, в точку С, потенциал которой равен 2000 В. Чему была равна скорость пылинки в точке А, если в точке
С она стала равной 5 м/с?

Дано: |
СИ |
m = 0,05 г |
5×10–5 кг |
q =100 нКл |
10–7 Кл |
ϕA = 6000 В |
|
ϕC = 2000 В |
|
vC = 5 м/с |
|
|
|
vA = ? |
|
|
|
q(jA |
- jC ) = |
mvC2 |
|
2 |
|||
|
|
Решение
Работа электрического поля по перемещению за-
ряда равна
A = q(ϕA −ϕC ) .
По теореме о кинетической энергии работа равна изме-
нению кинетической энергии тела
A = mvC2 - mvA2 . 2 2
Приравняв правые части этих выражений, получим
- mvA2 . 2
Выразив из полученного равенства кинетическую энергию заряда в точке А
mv A2 |
= |
mvC2 |
− q(ϕA − ϕC ) , |
2 |
|
||
2 |
|
||
найдем отсюда формулу для скорости в этой точке
vA = vC2 - 2q(jA - jC ) . m
Подставим в полученное равенство числовые значения
vA = |
(5 м/с) |
2 |
- |
2 ×10−7 Кл×(6000 В- 2000 В) |
|
= 3 |
м/с . |
|
|
5 ×10−5 |
кг |
||||||
|
|
|
|
|
|
|
||
§ 64
Напряженность как градиент потенциала. Эквипотенциальные поверхности
Найдем взаимосвязь между напряженностью электростатического поля, яв-
ляющейся его силовой характеристикой, и потенциалом – энергетической харак-
теристикой поля.
Работа по перемещению единичного точечного положительного заряда од-
ной точки в другую вдоль оси x при условии, что точки расположены бесконеч-

но близко друг к другу и x2 − x1 = dx , равна Exdx. Та же работа равна ϕ1 − ϕ2 = −dϕ. Приравняв оба выражения, можем записать
(64.1)
где символ частной производной подчеркивает, что дифференцирование произ-
водится только по x . Повторив аналогичное рассуждения для осей y и z , можем найти вектор E
R |
|
¶j R |
+ |
¶j R |
+ |
¶j R |
E = - |
i |
j |
k , |
|||
|
|
¶x |
|
¶y |
|
|
|
|
|
|
¶z |
||
где i , j , k – единичные векторы координатных осей x , y , z.
Из определения градиента следует, что
E = -gradj или E = -Ñj . |
(64.2) |
Эквивалентные поверхности – |
поверхности, во всех точках которых потенциал |
имеет одно и тоже значение.
Линии напряженности в случае точечного заряда перпендикулярны эквипотенци-
альным поверхностям. Линии напряженности всегда нормальны к эквипотенци-
альным поверхностям.
Электростатические силы, действующие на заряд, всегда направлены по нормалям к эквипотенциальным поверхностям. Следовательно, вектор E всегда нормален к эквипотенциальным поверхностям, а поэтому линии вектора E орто-
гональны этим поверхностям.
Эквипотенциальных поверхностей вокруг каждого заряда и каждой сис-
темы зарядов можно провести бесчисленное множество. Однако их проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотен-
циальными поверхностями были одинаковыми. Тогда густота эквипотенциаль-
ных поверхностей характеризует напряженность поля в разных точках. Там,
где эти поверхности расположены гуще, напряженность поля больше.

Зная расположение линий напряженностей электростатического поля, мож-
но построить эквипотенциальные поверхности и, наоборот, по известному распо-
ложению эквипотенциальных поверхностей можно определить в каждой точке поля величину и направления напряженности поля.
На рисунке изображены для примера виды линий напряженностей (штриховые линии) и эк-
випотенциальных поверхностей (сплошные ли-
нии) полей положительного точечного заряда (а)
и заряженного металлического цилиндра, имею-
щего на одном конце выступ, а на другом – впадину (б).
§ 65
Вычисление разности потенциалов по напряженности поля
1. Поле равномерно заряженной бесконечной плоскости определяется форму-
лой E = σ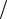 2ε0 , где σ – поверхностная плоскость заряда. Разность потенциалов между точками, лежащими на расстояниях x1 и x2 от плоскости равна
2ε0 , где σ – поверхностная плоскость заряда. Разность потенциалов между точками, лежащими на расстояниях x1 и x2 от плоскости равна
ϕ − ϕ |
|
= x2Edx = x2 |
σ |
dx = |
σ |
(x − x ) . |
||
|
|
2ε0 |
||||||
1 |
2 |
∫ |
∫ |
2ε0 |
2 |
1 |
||
|
|
|
|
|
||||
|
|
x1 |
x1 |
|
|
|
|
|
2. Поле двух бесконечных параллельных разноименно заряженных плоско-
стей определяется формулой E = σ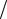 ε0 . Разность потенциалов между плоскостя-
ε0 . Разность потенциалов между плоскостя-
ми, расстояние между которыми равно d , равна
ϕ −ϕ |
|
= d Edx = d |
σ |
dx = |
σ |
d = Ed . |
(65.1) |
|||||||
|
|
|
||||||||||||
1 |
|
2 |
|
∫ |
∫ε |
|
|
ε |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
0 |
|
0 |
|
|
0 |
|
|
||
3. Поле равномерно заряженной сферической поверхности радиуса R с об- |
||||||||||||||
щим зарядом q вне сферы ( r > R ) вычисляется по формуле |
|
|||||||||||||
E = |
|
1 |
|
q |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
4πε0 r2 |
|
|
|
|
|
|
|
|
|||||

Разность потенциалов между двумя точками, лежащими на расстояниях r1 |
и r2 от |
||||||||||||||||
центра сферы ( r1 > R, |
r2 > R), равна |
|
|
|
|
|
|
|
|
||||||||
ϕ − ϕ |
|
= |
r2 |
Edr = |
r2 |
1 |
|
q |
dr = |
q |
|
|
1 |
− |
1 |
|
|
|
∫ |
∫ |
|
|
|
||||||||||||
|
|
|
|
. |
(65.2) |
||||||||||||
|
|
|
|
|
|
r |
|||||||||||
1 |
2 |
|
|
4πε r2 |
4πε r |
|
|
|
|||||||||
|
|
|
r |
|
r |
0 |
|
|
|
|
0 |
1 |
2 |
|
|
||
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Если принять r1 = r и r2 = ∞, то потенциал поля вне сферической поверхности,
задается выражением
ϕ = 1 q . 4πε0 r
Внутри сферической поверхности потенциал всюду одинаков и равен
ϕ = 1 q . 4πε0 R
График зависимости ϕ от r приведен на рисунке.
4. Поле объемно заряженного шара радиуса R с общим зарядом q вне шара
( r > R ) вычисляется по формуле
E = 1 q , 4πε0 r2
поэтому разность потенциалов между двумя точками, лежащими на расстояниях r1 и r2 от центра шара ( r1 > R, r2 > R), определяется формулой (65.2). В любой точке, лежащей внутри шара на расстоянии r′ от центра ( r′ < R ), напряженность определяется выражением
E = |
1 q |
r′. |
||
|
|
|
||
4πε0 R3 |
|
|||
Следовательно, разность потенциалов между двумя точками, лежащими на рас-
стояниях r1′ и r2′ от центра шара ( r1′ < R , r2′ < R), равна
′
ϕ1 − ϕ2 = r∫2′Edr = 8πεq0R3 (r2′2 − r1′2 ).
r1

5. Поле равномерно заряженного бесконечного цилиндра радиуса R , заря-
женного с линейной плоскостью τ, вне цилиндра ( r > R ) определяется формулой
E = |
τ |
|
. |
2πε |
|
||
|
0 r |
||
Разность потенциалов между двумя точками, лежащими на расстояниях r1 |
и r2 от |
||||||||||||||||
оси заряженного цилиндра ( r1 > R, r2 > R), равна |
|
||||||||||||||||
j - j |
|
= r2 |
Edr = |
|
t |
r2 |
dr |
= |
t |
|
ln(r |
r ). |
(65.3) |
||||
2 |
|
|
∫ |
|
|
|
|
||||||||||
1 |
|
∫ |
|
2pe0 |
|
r |
|
2pe |
2 |
1 |
|
||||||
|
|
|
r |
|
r |
|
|
0 |
|
|
|
||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Задача 1. Две бесконечные параллельные плоскости, находящиеся на рас- |
|||||||||||||||||
стоянии d = 4 |
мм, несут равномерно распределенные заряды с поверхностными |
||||||||||||||||
плотностями σ = 1 нКл/м2 и σ |
2 |
= −3 нКл/м2. Найти разность потенциалов между |
|||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскостями. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дано: |
|
|
|
|
СИ |
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
d = 4 мм |
|
|
|
|
0,004 м |
|
|
|
|
|
|
Разность потенциалов между двумя беско- |
|||||
s1 = 1 нКл/м2 |
|
|
|
10–9 Кл/м2 |
|
|
|
нечными параллельными плоскостями определя- |
|||||||||
s2 = -3 нКл/м2 |
|
|
3×10–9 Кл/м2 |
|
|
ется по формуле |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ1 − ϕ2 = Ed , |
|
|||
ϕ1 − ϕ2 = ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где E – напряженность электрического поля между плоскостям, которое является однородным.
Как видно из рисунка, вектора напряженности элек-
трических полей E+ положительно и E− отрицательно за-
ряженных плоскостей в области между плоскостями на-
правлены в одну сторону, и из величины равны, соответственно,
E+ = σ1 и E− = σ2 . 2e0 2ε0

Тогда результирующий вектор напряженности электрического поля между плос-
костями равен по величине
s + s E = E+ + E− = 12e0 2 .
Подставим это выражение в формулу для разности потенциалов
j - j = |
s1 + |
|
s2 |
|
|
d . |
|
|
|
||||||
|
|
||||||
|
|
|
|
|
|||
1 |
2 |
2e0 |
|||||
|
|
|
|
|
|
||
В полученное равенство подставим числовые значения
|
|
|
10−9 |
Кл/м2 |
+ 3×10−9 Кл/м2 |
|||
j - j |
|
= |
|
|
|
|
|
×0,004 м = 0,9 В. |
|
|
|
2 ×8,85 |
×10−12 |
|
|||
1 |
2 |
|
|
|
Ф/м |
|||
|
|
|
|
|
|
|
||
Задача 2. Найдите потенциал в центре металлической сферы радиуса R = 5
см, равномерно заряженной по поверхности с поверхностной плотностью заряда σ = 5 нКл/м2, если на бесконечности он равен нулю.
Дано: |
СИ |
|
|
|
|
Решение |
R = 5 см |
0,05 м |
Во |
всей |
|
области внутри сферы r ≤ R про- |
|
s = 5 нКл/м2 |
5×10–9 Кл/м2 |
странство является эквипотенциальным, то есть |
||||
ϕ∞ = 0 |
|
j = |
1 |
|
q |
|
|
4pe0 |
|
R , |
|||
|
|
|
||||
ϕ = ? |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где q – заряд сферы, который равен
q = sS = s4pR2 .
Подставим это выражение в формулу для потенциала
j = |
1 s4pR2 |
= |
sR |
||
|
|
. |
|||
4pe0 R |
|||||
|
|
e0 |
|||
По полученному равенству рассчитаем числовое значение потенциала
j = |
5 ×10−9 |
Кл/м2 |
×0,05 м |
= 28 |
В. |
|
8,85×10−12 |
Ф/м |
|||||
|
|
|
||||

Задача 3. Напряженность однородного электрического поля в некоторой точке равна 300 В/м. Вычислите разность потенциалов между этой точкой и дру-
гой, лежащей на прямой, составляющей угол 30° с вектором напряженности. Рас-
стояние между точками равно 3 мм.
Дано: |
|
СИ |
Решение |
d = 3 мм |
0,003 м |
Разность потенциалов в одно- |
|
E = 300 В/м |
|
родном электрическом поле между |
|
α = 30° |
|
|
двумя точками, не лежащими на од- |
|
|
|
|
j1 - j2 = ? |
|
ной силовой линии, можно найти |
|
|
|
|
по формуле |
|
|
|
|
j1 |
- j2 = Ed cos a . |
||
Подставим числовые значения |
|||
j1 |
- j2 = 300 В/м×0,003 м×cos 30° = 0,78 В. |
||
§ 66
Типы диэлектриков. Поляризация диэлектриков
Молекулы в диэлектриках можно
рассматривать, как диполь с электрическим моментом равным
R =
p q l .
Диэлектрики – это вещества, которые не прово-
дят (плохо проводят) электрический ток.
Первую группу диэлектриков (N2, H2, O2, CO2, CH4, …) составляют вещест-
ва, молекулы которых имеют симметричное строение, т.е. центры «тяжести» по-
ложительных и отрицательных зарядов в отсутствии внешнего электрического
поля = 0 совпадают и, следовательно, R i = 0 . Молекулы таких диэлектриков p
E
называются неполярными. Под действием электрического поля E ¹ 0 заряды не-

полярных молекул смещаются в противоположные стороны и молекулы приобре-
тают дипольный момент.
Поляризацией диэлектрика называется процесс ориентации диполей или появ-
ления под воздействием электрического поля ориентированных по полю диполей.
У неполярных молекул наблюдается электронная или деформационная поля-
ризация, заключающаяся в возникновение у атомов индуцированного электриче-
ского момента p за счет деформации электронных орбит.
Вторую группу диэлектриков (H2O, NH3, SO2,
CO, …) составляют вещества, молекулы которых имеют асимметрическое строение, т.е. центры
«тяжести» положительных и отрицательных заря-
дов не совпадают. Таким образом, эти молекулы в отсутствии E = 0 обладают pi ¹ 0 . Молекулы та-
ких диэлектриков называются полярными. Однако в отсутствии внешнего элек-
трического поля ∑ R i = 0 , так как из-за теплового движения i молекулы ори-
E
p
p
i
ентируются в пространстве хаотически. Если такой диэлектрик поместить во
внешнее ¹ 0 , то i стремятся ориентироваться вдоль поля, и тогда ∑ R i ¹ 0 . У
E p p
i
полярных молекул наблюдается ориентационная или дипольная поляризация
диэлектриков, которая заключается в ориентации имеющихся pi по полю. Эта ориентация тем сильнее, чем больше величина E .
Третью группу диэлектриков (NaCl, KCl, KBr, …) составляют вещества, мо-
лекулы которых имеют ионное строение. Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. В
этих кристаллах нельзя выделить отдельные молекулы, а рассматривать их можно как систему двух вдвинутых одна в другую ионных подрешеток. При наложение на ионный кристалл внешнего электрического поля E происходит некоторая де-
формация кристаллической решетки или относительное смещение подрешеток,
приводящее к возникновению дипольных моментов p . У ионных решеток на-
