
mehanika_spl.sr.tekst_lekciy_popov_savich
.pdfJ |
II |
|
1 |
T T |
jj |
T T , |
(2.38) |
||
|
|||||||||
|
|
2 |
|
ii |
ij ij |
||||
|
|
|
|
|
|
|
|
|
|
|
JIII |
|
Tij |
|
detTij , |
(2.39) |
|||
носят название первого, второго и третьего инварианта тензора Tij . Три корня кубиче-
ского уравнения (2.36), обозначенные называются главными значе-
ниями тензора Tij . У симметричного тензора с действительными компонентами глав-
ные значения действительны; если все они различны, то три главных направления взаимно ортогональны. В главных осях таблицы из компонент тензора приводятся к диагональной форме:
|
(1) |
0 |
0 |
|
|
|
|
|
|||
T |
0 |
(2) |
0 |
. |
(2.40) |
|
0 |
0 |
|
|
|
|
|
|
(3) |
|
|
Если (1) |
(2) , |
то диагональный вид тензора не |
зависит от выбора осей, соответст- |
вующих |
(1) и |
(2) , и нужно установить только |
главную ось, соответствующую (3) . |
Если все главные значения равны, то любое направление является главным. Если
главные значения упорядочены, то принято |
|
обозначение |
их через |
(1) , |
(2), |
(3) и |
||||||||||||||
располагать их в порядке убывания: (1) |
(2) |
(3) . |
|
|
|
|
|
|
|
|||||||||||
|
Преобразование от системы |
Ox x x |
к системе главных осей |
Ox x x |
дается |
|||||||||||||||
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
||
таблицей, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
x2 |
|
|
x3 |
|
|
|
|
|
|
|
|
x |
|
a |
n(1) |
|
a |
n(1) |
|
a13 |
n3(1) |
|
|
|
|
|
|||
|
|
|
1 |
|
|
11 |
|
1 |
|
|
12 |
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
a |
21 |
n(2) |
|
a |
22 |
n( 2) |
|
a23 |
n3(2) |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
x |
|
a |
n(3) |
|
a |
n(3) |
|
a |
n(3) |
|
|
|
|
|
|||
|
|
|
3 |
|
|
31 |
|
1 |
|
|
32 |
2 |
|
33 |
3 |
|
|
|
|
|
где |
n( j) |
- направляющие косинусы |
|
jго |
|
главного направления. |
|
|
|
|
||||||||||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21

Лекция 3
Кинематика деформируемой среды
3.1.Переменные Лагранжа и Эйлера и связь между ними
Ввыделенном объекте сплошной среды каждая его частица в фиксированный момент времени t=0, имеет координаты X1, X2, X3. Эти координаты или какие-то другие параметры,
которое являются функциями этих координат, дают возможность отличить одну точку континуума от другой. В разные моменты времени t различные точки сплошной среды характеризуются четырьмя независимыми параметрами X1, X2, X3,t , которые называется перемен-
ными Лагранжа.
Для задания движения континуума в переменных Лагранжа достаточно задать декартовы координаты xi всех его точек или радиус вектор r , как функции четырёх переменных Ла-
гранжа
xi xi (X1,X2, X3,t), или |
r |
|
r |
( |
r0,t). |
(3.1) |
В кинематике одной точки переменные X1, X2, X3 |
не применялись, так как не было дру- |
|||||
гих точек, от которых следовало отличать рассматриваемую точку. Там координаты точки зависели только от времени xi xi(t), или r r(t). Для сплошной среды задание парамет-
ров X1, X2, X3 позволяет выделить конкретную точку. Разным значениям этих параметров
соответствуют различные точки континуума.
В механике сплошной среды чаще используются переменные Эйлера. В методе Эйлера рассматриваются не фиксированные частицы континуума, а точки пространства занятые сплошной средой. За независимые переменные принимают время t и декартовы координаты точек пространства x1,x2, x3. Четыре независимые переменные величины t, x1,x2,x3 называ-
ются переменными Эйлера.
Различные векторные и скалярные величины, характеризующие сплошную среду, как например, скорость, ускорение, плотность и т.д., рассматриваются как функции этих перемен-
ных. |
|
|
Установим связь между переменными Лагранжа и Эйлера. |
|
|
По определению проекции скорости, имеем |
|
|
i i (x1,x2,x3,t) |
(i 1,2,3). |
(3.2) |
Такое представление определяет поле скоростей в данной области пространства в любой момент времени. В результате интегрирования уравнений (3.2) появляется три постоянных
интегрирования c1,c2,c3 и интегралы представятся в виде |
|
|
xi xi (t;c1,c2,c3) (i 1,2,3). |
|
(3.3) |
Рассматривая переменные Лагранжа Xi как значения xi |
при t0 0, |
получим систему |
уравнений |
|
|
Xi Xi (to;c1,c2,c3) (i 1,2,3). |
|
(3.4) |
Разрешая которую относительно ci можно выразить c1,c2 и |
c3 через Xi |
после чего урав- |
нения (3.3) примут вид уравнений (3.1). |
|
|
Для существования взаимной связи между переменными Лагранжа и Эйлера необходимо и достаточно что бы определитель (det), называемый якобианом был отличен от нуля.
22

|
|
|
|
x1 |
|
x1 |
|
x1 |
|
|
|
xi |
|
|
X1 |
|
X2 |
|
X3 |
|
|
J |
|
|
x2 |
|
x2 |
|
x2 |
0. |
||
X j |
X1 |
X2 |
X3 |
|||||||
|
|
|
|
|
|
|||||
|
|
|
|
x3 |
|
x3 |
|
x3 |
|
|
|
|
|
|
X1 |
|
X2 |
|
X3 |
|
3.2. Перемещения, скорости и ускорения точек континуума.
Вектором перемещения u точки М из некоторого начального положения Мo с радиус-
вектором ro в текущее положение М с радиус-вектором r называют вектор определяемый формулами
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
r |
|
ro, или ui |
xi Xi. |
|
|
|
|
|
|
|
|
|
|
|
(3.5) |
|
|||||||||||||||||||||||||||||||||
Начальный радиус-вектор |
ro (рис.3.1.) выражается через переменные Лагранжа Xi |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Mo |
|
u |
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
ro X1eˆ1 |
X2eˆ2 X3eˆ3, |
|
|
|
|
|
|
|
|
|
|
|
(3.6) |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
конечный |
r |
-через переменные Эйлера |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
x1eˆ1 x2eˆ2 x3eˆ3. |
|
|
|
|
|
|
|
|
|
|
|
(3.7) |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обычно проекции перемещений (ui ) частиц среды |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рассматриваются как функции координат начальных |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
их положений, тогда по (3.5) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис.3.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi Xi ui (X1, X2, X3;t). |
|
|
|
|
|
|
(3.8) |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
dxi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение поля скоростей дано формулой (3.2) в |
|||||||||||||||||||||||||||||||||||||||||||||
виде |
|
|
|
|
|
(x ,x |
|
,x ;t), |
|
|
или |
|
|
|
|
|
|
|
dr |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.9) |
|
||||||||||||||||||||||||||||||||
i |
i |
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dt |
|
1 |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Другое определение того же вектора можно получить если учесть (3.8), так что |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i |
dxi |
|
|
d |
(Xi |
ui) |
dui |
, |
|
или |
|
|
|
|
|
|
dr |
|
|
d( |
ro |
u |
) |
|
|
du |
, |
|
|
|
|
|
|
|
|
|
|
|
(3.10) |
|
|||||||||||||||||||||||||||||||||||||||||||||
V |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
dt |
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
так как |
ro |
X1eˆ1 |
X2eˆ2 |
X3eˆ3 не зависит от времени. Если в (3.10) перемещение выразить в |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
лагранжевых переменных ui ui (X1, X2, X3;t), то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ui(X |
1, X2, X3;t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
( |
ro,t) |
|
|
u |
( |
ro,t) |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
ui(X1 |
, X2, X3;t) |
|
|
|
|
|
|
|
|
, |
|
или |
|
V u |
|
|
|
|
|
. |
(3.11) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i ui |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
t |
|
|
|||||||||||||||||||||||||||||||
Если перемещение задано в Эйлеровой форме ui |
|
ui(x1,x2,x3;t), то |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dui (x1,x2, x3;t) |
|
|
|
ui (x1,x2,x3;t) |
|
|
|
|
|
|
ui(x1,x2,x3;t) |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x1,x2,x3;t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j (x1,x2,x3;t) |
, |
||||||||||||||||||||||||||||||||||
i (x1,x2,x3;t) ui |
|
|
|
|
|
|
dt |
|
|
|
|
|
t |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xj |
|||||||||||||||||||
|
|
|
|
( |
|
,t) |
u |
( |
|
,t) |
du |
( |
r |
,t) |
|
|
u |
( |
r |
,t) |
|
|
( |
|
,t) |
|
|
|
( |
|
,t), |
|
|
|
|
|
|
|
|
|
|
|
(3.12) |
|
|||||||||||||||||||||||||||||||||||||||||
или V |
r |
r |
V |
r |
|
u |
r |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
где второе слагаемое правой части появляется из-за того, что частица меняет своё положение
впространстве. Первое слагаемое правой части (3.12) характеризует скорость в фиксированной точке пространства и называется локальной (или местной) скоростью. Второй член (3.12) называется конвективной скоростью, так как он выражает вклад, обусловленный движением частиц в переменном поле скоростей.
Материальная производная от скорости по времени есть ускорение. Если скорость задана
влагранжевой форме (3.11), то
|
|
|
d i |
|
i |
|
|
|
dV |
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ai |
|
|
|
|
|
, или a V |
|
|
|
|
(3.13) |
|||
|
|
|
|
|
. |
|||||||||
i |
dt |
t |
||||||||||||
|
|
|
dt |
|
t |
|
|
|
|
|
|
|
||
Если же скорость выражена в эйлеровой форме (3.12), то
23

ai |
|
d i |
|
|
|
i |
j |
i |
, |
|
||||||||||||
|
dt |
|
t |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
xj |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
a |
|
dV |
|
|
V |
|
|
|
|
|
|
|
|
||||||||
|
|
V |
V . |
(3.14) |
||||||||||||||||||
|
dt |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|||||
3.3. Линии тока и траектории. Трубка тока
Поле скоростей является однородным, если векторы скоростей во всех точках поля одинаковы. Поле называется стационарным, если оно не меняется с течением времени, т.е.
V 0. В противном случае – нестационарным. В разделе кинематика сплошной среды поле
t
скоростей считается заданным.
Траекторией называется линия, по которой следует частица в процессе её движения или течения. Линией тока для поля скоростей в некоторый момент времени называется линия, касательная к которой в любой точке совпадает по направлению со скоростью в этой точке
(рис.3.2). Из условия, что вектор скорости V в данной точке, направлен по касатель- |
|
|||||||||||||||||||
|
|
|
|
|
ной к линии тока, следует, что дифференциал dr |
ра- |
||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
dr |
V диус-вектора этой точки и V |
имеют общее направле- |
||||||||||||||||
|
|
|
|
ние, запишем векторное равенство, выражающее ус- |
||||||||||||||||
M |
|
|
ловие параллельности этих векторов |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
V dr 0, |
|
|
|
(3.15) |
|||||||||||
|
r |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
что в проекциях на оси координат даёт систему трёх |
||||||||||||||||
|
|
|
|
|
дифференциальных уравнений |
|
|
|
|
|||||||||||
|
|
|
|
|
|
2dx3 3dx2 0, |
|
|
|
|
||||||||||
|
|
|
|
|
|
3dx1 |
1dx3 |
0, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
откуда получим |
|
|||||||||||||
|
|
|
|
|
|
dx |
|
|
dx |
0, |
|
|
|
|
|
|||||
|
|
O |
Рис.3.2. |
1 2 |
|
|
|
2 1 |
|
|
|
dx3 |
|
|
|
|||||
|
|
|
|
dx1 |
|
|
|
|
|
dx2 |
|
|
. |
|
(3.16) |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1(x1,x2,x3) |
|
|
|
|
|
|
3(x1,x2,x3) |
|
|||||||
|
|
|
|
|
2(x1,x2, x3) |
|
|
|
||||||||||||
Дифференциальные уравнения траекторий будут аналогичны уравнениям (3.16) линий тока, но с тем отличием, что теперь уже и время t будет таким же независимым переменным, как x1,x2,x3 и дифференциональное уравнение траектории запишется в виде
dx1 |
|
dx2 |
|
dx3 |
. |
(3.17) |
|
1(x1,x2,x3;t) |
2(x1,x2,x3;t) |
3(x1,x2,x3;t) |
|||||
|
|
|
|
Если поле скоростей стационарно, то время t не будет входить в проекции скоростей, ис-
чезнет оно и из уравнения (3.17), и они совпадут с |
уравнениями (3.16). Отсюда |
|||
следует, что в стационарных полях скоростей |
траектории и линии тока |
|||
в любой момент времени совпадают. |
|
|
||
Проводя в данный момент времени |
через |
точки замкну- |
||
того контура |
|
(рис.3.3) линии |
тока, |
получим |
поверхность |
|
тока, |
заключающую внутри себя |
|
часть жидкости, называемую |
трубкой тока. В любой точке |
|||
поверхности |
тока |
вектор |
скорости V |
направлен по |
касательной |
к |
линии |
тока, так что среда не проникает |
|
сквозь поверх- |
|
ность тока. |
|
|
Рис.3.3.
24

3.4. распределение скоростей в элементарном объёме среды.
Пространственный градиент мгновенного поля скорости даёт тензор градиента скорости
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
||||
|
|
i |
|
|
|
x1 |
|
|
|
x2 |
|
|
|
x3 |
|
|
|
|
|
|
|
|
||
Y |
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
, или |
|
|
|
|
|||||||
|
|
|
|
|
|
|
Y V |
. |
(3.18) |
|||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
ij |
|
x |
j |
|
|
|
x |
|
|
|
x |
2 |
|
|
|
x |
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
x1 |
|
|
|
x2 |
|
|
|
x3 |
|
|
|
|
|
|
|||
Этот тензор можно разложить на симметричную и антисимметричную части следующим
образом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
i |
|
|
|
|
|
1 |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Y |
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
j |
, |
или |
|
Y |
V V |
|
V V . |
(3.19) |
|||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
ij |
2 |
|
x |
j |
i |
|
2 |
|
|
x |
j |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Симметричный тензор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
D D |
|
|
|
|
|
|
|
j |
, |
или |
|
D |
V V , |
(3.20) |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ij |
|
|
|
ji |
|
|
|
2 |
|
|
x |
j |
|
|
i |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
называется тензором скоростей деформации. Антисимметричный тензор |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
i |
|
|
|
j |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
V |
|
V |
|
|
|
|
|
|
|
|
|
|
или |
V |
|
(V V ), |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
|
|
|
x |
|
|
, |
2 |
|
(3.21) |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ij |
|
|
|
ji |
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
называется тензором завихренности.
Дадим физическую интерпретацию этих тензоров. Для этого выделим две соседние точки
M и N движущегося объёма сплошной среды (Рис.3.4.) скорости этих точек обозначим |
|
|||||||||||||||||||||||||
x 3 |
|
|
i и i d i соответственно. |
Таким обра- |
||||||||||||||||||||||
|
|
зом, скорость точки N относительно точки |
||||||||||||||||||||||||
|
|
|
|
M равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
N |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
i |
d i xj |
dxj , |
или dV V dr, |
|
|
(3.22) |
|||||||||||||||||||
|
dxj |
|
|
|||||||||||||||||||||||
|
где частные производные |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
M |
|
|
d i |
i |
dx1 |
|
i |
|
i |
dx3 |
|
i |
dxj , |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
x |
2 |
|
|
x |
3 |
|
|
|
|
|
x |
j |
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x2 |
вычисляются в точке M. Выражение (3.22) |
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
можно записать через D |
и V : |
|
|
|
|||||||||||||||||||
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ij |
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
d |
i |
(D |
V )dx |
, или |
|
|
|
|
|
|
|
||||||||||||
|
Рис.3.4. |
|
|
|
|
|
|
ij |
|
ij |
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
(3.23) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dV (D V) dr.
Если тензор завихренности обращается в нуль (Vji 0), то поле скоростей называется “без-
вращательным” (безвихревым).
Если же тензор скоростей деформаций тождественно равен нулю (Dij 0), то выражение
(3.23) примет вид
d i Vijdxj, |
или |
dV V dr |
. |
(3.24) |
||||||||
Сопутствующий тензору завихренности вектор определяется соотношением |
|
|||||||||||
q |
|
k |
, |
или |
|
|
|
|
|
|
|
(3.25) |
|
q |
V, |
||||||||||
|
|
|||||||||||
i |
ijk xj |
|
|
|
|
|
|
|
|
|
||
и называется вектором завихренности.
25
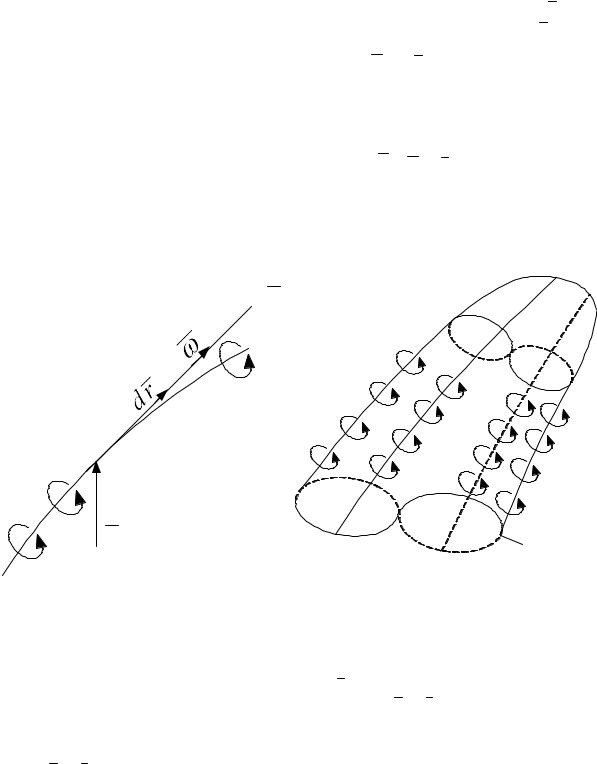
Символическая форма записи (3.25) |
показывает что вектор завихренности |
q |
получается |
||||||||||||||||||||
действием оператора rot на поле скоростей. Вектор, равный половине вектора |
q |
|
|
||||||||||||||||||||
|
1 |
q |
|
|
1 |
|
|
k |
, или |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
V |
, |
|
(3.26) |
||||||||||||||
2 |
|
|
|
|
|
||||||||||||||||||
i |
|
i |
2 |
|
ijk xj |
2 |
2 |
|
|
|
|
|
|
|
|
||||||||
называется вектором вихря скорости. При вращении абсолютно твёрдого тела, относительная скорость частицы, соседней с M и находящийся от неё на расстоянии dxj , даётся форму-
лой
d i ijk jdxk , или dV dr. (3.27)
Линия касательная к которой в каждой точке движущейся среды направлена по вектору вихря скорости называется вихревой. На рисунках вихревые линии обозначаются закругленной стрелкой. Если провести через точки некоторого замкнутого контура вихревые линии, то получим вихревую поверхность, а ограниченную ею часть жидкости, участвующую во вращении называют вихревой трубкой (рис.3.5). В стакане
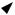 q
q
М
r |
Рис.3.5. |
а |
воды можно наблюдать вихревые трубки, если быстро вынуть ложку после кругового размешивания ею воды в стакане.
Самыми грозными вихревыми трубками являются смерчи. Они опираются своими нижними концами на поверхность, воды или суши, а верхними уходят в слои облаков нависших над поверхностью суши или моря.
Получим уравнение вихревой линии. Пусть dr - бесконечно малый вектор в направлении вектора завихренности (вихря) скорости (рис.3.5). тогда q dr 0. Раскрывая это векторное произведение через определитель, получим
|
|
|
eˆ1 |
eˆ2 |
eˆ3 |
(q2dx3 q3dx2)eˆ1 (q3dx1 q1dx3)eˆ2 (q1dx2 q2dx1)eˆ3 0, |
|||||||
q |
dr |
|
q1 |
q2 |
q3 |
||||||||
|
|
|
dx1 dx2 dx3 |
|
|
|
|
|
|
|
|
||
откуда следует, что |
|
|
|
dx1 |
|
dx2 |
|
dx3 |
|
|
|||
|
|
|
|
|
|
|
|
|
. |
(3.28) |
|||
|
|
|
|
|
|
|
q1 |
q2 |
|
||||
|
|
|
|
|
|
|
|
|
q3 |
|
|||
Это есть дифференциальное уравнение вихревой линии.
Компоненты тензора скоростей деформации имеют следующий физический смысл. Диагональные элементы (D11,D22,D33) это скорости относительного удлинения отрезков, распо-
26
ложенных вдоль осей координат. Так для чистой деформации из (3.23) когда Vji 0 следует,
что
d i |
Dijdxj , или |
dV D dr |
. |
(3.29) |
Недиагональные элементы Dij характеризуют скорость сдвига и являются мерой скоро-
сти изменения прямых углов между направлениями отрезков, расположенных вдоль осей координат. Вследствие того что Dij является симметричным тензором второго ранга, для него
существуют такие понятия, как главные оси, главные значения, инварианты,(поверхности скоростей деформации) и девиатор скоростей деформации.
Вмеханике жидкости и газа деформационная составляющая движения не имеет большого значения. Компоненты тензора скоростей деформации встречаются только в динамике вязких жидкостей и газов.
Вобщем случае каждой частице движущейся среды сопоставляются два вектора: вектор
скорости V и угловой скорости . Каждому из этих двух векторов соответствуют свои век-
торные линии: вектору V - линии тока, векторам q и - вихревые линии (рис.3.6.)
q
M
 V
V
Рис.3.6.
27

Лекция 4
Распределение сил в сплошной среде. Равенства Коши.
1.Объемные и поверхностные силы
Вдинамике сплошных сред выделяют два класса сил действующих на частицы среды: объемные (массовые) и поверхностные. Объемные силы это силы, которые действуют на элементы объема (силы веса, тяготения, инерции, электростатические, электромагнитные). К поверхностным силам относят силы, действующие на элементы поверхности, ограничивающей объем.
Вдинамике сплошной среды имеют дело не с самими силами, а с плотностями их распределения в пространстве.
Под средней плотностью распределения сил, приложенных в точках сплошной среды,
понимают отношение главного вектора сил Rоб , приложенных в точках объема этого объема m ср . Назовем это отношение средней объемной силой
|
|
|
R |
об |
|
R |
об |
|||
fср |
||||||||||
|
|
|
|
|
, |
|||||
|
|
|
|
|||||||
|
|
m |
ср |
|||||||
а объемная сила в данной точке есть предел этого отношения
|
|
|
|
|
R |
об |
|
|
R |
об |
|||||
f |
|
|
|
|
|||||||||||
lim |
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|||||||||
|
0 |
ср |
|
|
|||||||||||
|
|
ср |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к массе
(4.1)
(4.2)
(4.3)
Так, например, объемной силой для сил тяжести будет служить вектор ускорения g свобод-
ного падения, для инерционной, центробежной силы - центробежное ускорение 2r , где r - вектор, направленный по кратчайшему расстоянию от точки приложения центробежной силы до оси в сторону от оси.
Аналогично, среднюю плотность распределения поверхностных сил определяют
как отношение главного вектора Rпов поверхностных сил к площади этой поверхности S , на которой эти силы действуют, и называют средним напряжением:
|
|
|
p |
|
|
|
R |
пов |
|
|
|
|||||
|
|
|
|
|
|
|
|
. |
|
|
|
(4.4) |
||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
S |
|
|
|
||||||
Переходя к пределу путем стягивания площадки S |
в данную точку поверхности, полу- |
|||||||||||||||
чим вектор напряжения в этой точке, равный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
пов |
|
|
|
|
пов |
|
||||
|
p |
|
|
R |
|
|
R |
|
||||||||
|
lim |
|
|
|
|
|
|
|
|
|
. |
(4.5) |
||||
|
S |
|
|
|
||||||||||||
|
|
S 0 |
|
|
|
S |
|
|||||||||
Напряжение имеет размерность (Н/м2) и выражается в «паскалях».
Из (4.5) следует, что элементарная поверхностная сила в данной точке сплошной среды
равна |
|
Rпов p S, |
(4.6) |
т.е. равна произведению напряжения p в данной точке на площадь элементарной площадки
S .
Главные векторы объемных и поверхностных сил, приложенных к конечным объемам или к конечным поверхностям S , определяют суммированием элементарных, объемных или поверхностных сил соответственно по объему или поверхности S . В сплошной среде с
28
непрерывными распределениями объемных и поверхностных сил такие силы определяются объемными или поверхностными интегралами.
Отметим основное различие (кроме несовпадения размерностей) между векторами
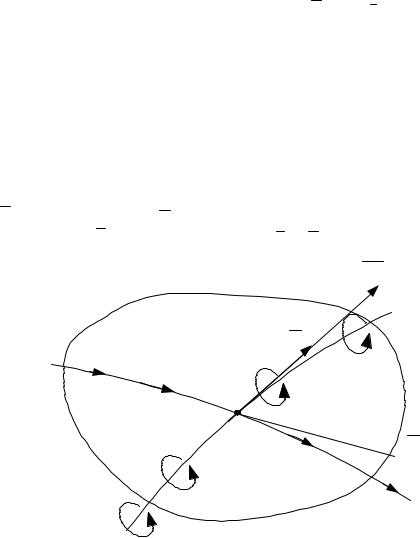
f и p : в то время как вектор f является однозначной векторной функцией точек пространства и времени f f (r,t), т.е. образует векторное поле, вектор p принимает в каждой точке пространства бесчисленное множество значений в зависимости от ориентации площадки, к которой приложено напряжение, и, таким образом, векторного поля не образует.
Определим ориентацию элементарной площадки S в точке М ортом нормали nˆ к плоскости площадки (рис.4.1). У площадки имеются две стороны.
|
|
|
|
|
|
|
|
Ту из них, к которой приложен орт nˆ , назовем |
||||||
|
|
|
nˆ |
лицевой, а другую - тыльной. Вектор напряже- |
||||||||||
|
|
|
|
|
|
|
|
ния, приложенный к лицевой стороне |
||||||
|
|
|
|
|
|
|
|
обозначим через |
p |
n . Тогда по закону действия и |
||||
|
|
|
|
p |
|
|
противодействия, напряжение приложенное к |
|||||||
|
|
|
|
n |
тыльной стороне площадки, будет равно |
|||||||||
|
|
|
|
|
|
|
|
|
p |
n' |
p |
n . Выбор одной из сторон площадки за |
||
|
|
|
|
|
|
|
|
|
||||||
pn |
S |
|
||||||||||||
лицевую, конечно, произволен, но наличием ор- |
||||||||||||||
|
|
|
|
|
|
|
|
та нормали лицевая сторона фиксируется, и в |
||||||
|
|
|
S |
дальнейшем рассуждении это наименование за |
||||||||||
|
|
|
|
|
|
|
|
ней сохранится. |
||||||
|
|
|
2. Равенства Коши. Тензор напряжений. |
|||||||||||
Докажем, что вектор напряжения |
p |
n |
можно представить как произведение орта nˆ , харак- |
|||||||||||
теризующего ориентацию площадки S |
в пространстве, на тензор второго ранга Р, являю- |
|||||||||||||
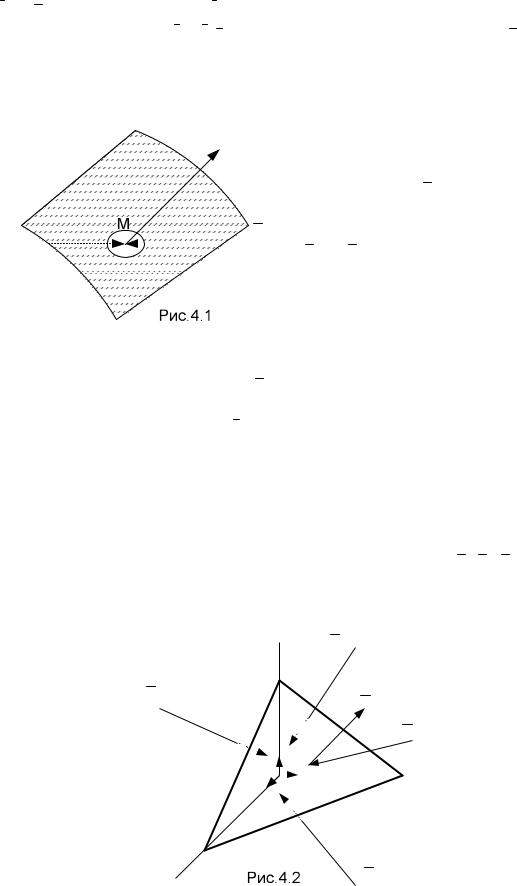
щийся функцией вектор - радиуса r точки и времени, т.е. образующий тензорное поле.
С этой целью выделим в среде элементарный тетраэдр MM1M2M3 (рис.4.2) с вершиной в данной точке М, с основанием в форме треугольника M1M2M3 , образованного пересечением наклонной плоскости с тремя координатными плоскостями, и боковыми граням, расположенными в координатных плоскостях. Обозначим площадь треугольника M1M2M3 через
S , а площади боковых граней соответственно - S1, S2, S3 , причем
индексы 1,2,3, при этих площадках, так же как и при напряжениях p1, p2, p3 , приложенных к этим площадкам, обозначают координатные оси перпендикулярные к площадкам.
|
|
M 3 |
|
X3 |
|
p |
1 S1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
p |
2 S2 |
|
|
|
|
n |
|
||||||
|
|
|
|
|
|
eˆ3 |
|
|
|
|
|
p |
n Sn |
|
|
|
M |
|
|
|
|
|
|
|
X 2 |
|
|||
|
||||||||||||||
|
|
eˆ1 |
|
|
|
eˆ2 |
|
|
|
|
M2 |
|||
|
|
|
|
|
|
|
|
|||||||
|
|
i1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
M1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
X1 |
|
|
|
|
|
p |
3 S3 |
|||||
29

Рассмотрим бесконечно малый тетраэдр как «жидкий», т.е. состоящий из частиц движущейся среды и напишем уравнение движения центра инерции этой системы частиц, общая масса которых пусть равна m; будем иметь
ac m f m pn Sn p1 S1 p2 S2 p3 S3.
где ac - ускорение центра инерции тетраэдра, f - плотность распределения объемных сил, а pn, p1, p2, p3 - векторы напряжений, приложенные к граням тетраэдра.
Лицевыми, очевидно, являются те, со стороны которых расположен орт nˆ и орты eˆ1,eˆ2 ,eˆ3
(чтобы не вводить новых). При последних трех членах в правой части последнего уравнения стоят знаки минус, так как к внешним - тыльным сторонам боковых граней
приложены напряжения p1, p2, p3 .
В рассматриваемом уравнении член слева и первое слагаемое справа как величины третьего порядка малости - они содержат элементы массы, пропорциональные объему - можно опустить по сравнению с остальными членами, содержащими элементы поверхностиSn , S1, S2, S3 , являющимися малыми второго порядка. Тогда оставляя лишь малые второго порядка, будем иметь
p |
n Sn |
p |
1 S1 |
p |
2 S2 |
p |
3 S3. |
(4.7) |
Замечая, что S1, S2, S3 являются проекциями площадки Sn на координатные плоско-
сти и, обозначая косинусы углов между ортом nˆ нормали к наклонной площадке и осями координат, представляющими нормали к координатным площадкам, через n1,n2,n3 ,
|
n |
cos(nˆ,eˆ ) |
получим |
1 |
1 |
n2 |
cos(nˆ,eˆ2 ) |
|
|
|
cos(nˆ,eˆ3 ) |
|
n3 |
|
S1 |
Sn cos(nˆ,eˆ1) n1 Sn , |
|
S2 |
Sn cos(nˆ,eˆ2 ) n2 Sn , |
|
S3 |
Sn cos(nˆ,eˆ3 ) n3 Sn. |
|
Подставляя эти значения S1, S2 |
, S3 в правую часть (4.7) |
сокращая на Sn |
и, стягивая |
|||||||
тетраэдр к его вершине в точке М получим точное выражение |
|
|
||||||||
|
p |
n n1 |
p |
1 n2 |
p |
2 n3 |
p |
3. |
|
(4.8) |
Проектируя обе части (4.8) на оси координат, придем к системе трех равенств: |
|
|||||||||
pn1 |
n1 p11 n2 p21 n3 p31, |
|
|
|||||||
pn2 n1 p12 n2 p22 n3 p32 , |
|
(4.9) |
||||||||
pn3 |
n1 p13 n2 p23 n3 p33. |
|
|
|||||||
В этих равенствах первый индекс при p отмечает принадлежность напряжения к пло-
щадке, перпендикулярной к данной оси координат, второй ось проекций; так, например, p31
обозначает проекцию на ось x1 напряжения, приложенного к площадке, перпендикулярной к оси x3 .
Величины с одинаковыми индексами p11, p22 , p33 , представляющие проекции векторов напряжений p1, p2, p3 на нормали к соответствующим площадкам, называются нормальными напряжениями, а проекции p12, p21,..., p31,... на оси, лежащие в плоскости площадок, - каса-
тельными напряжениями.
Система равенств (4.8) или (4.9) показывает, что проекции физически объективного вектора pn на оси координат являются линейными функциями проекций на те же оси физически
объективного вектора n . Коэффициенты в этой линейной связи представляют совокупность девяти величин.
30
