mehanika_spl.sr.tekst_lekciy_popov_savich

Таблица (4.10) не удовлетворяет принятому порядку индексов: первый - номер строки, второй - столбец. Поэтому за тензор напряжений примем тензор Р с таблицей

а тензору с таблицей (4.10) сопоставим тензор Pc , сопряженный с тензором Р. (отличающийся порядком индексов pik pki*C ).

В дальнейшем покажем, что различие между тензорами. P и P* отсутствует, поэтому операции умножения вектора на тензор справа или слева равны и формулы (4.9) можно переписать в тензорной форме так:

Эта форма равенств Коши не зависит от выбора системы координат (1827 г.)

Тензор второго ранга - это величина, определяемая в любой системе координат девятью числами (или функциями) pik , которые при изменении системы координат преобразуются в

pik' по закону

В сопротивлении материалов и некоторых других технических курсах принимают следующие обозначения для нормальных и касательных напряжений

p11 1, p22 2, p33 3, p12 12, p23 23.

и т.д.

3. Теорема о взаимности касательных напряжений

Для равновесия тетраэдра MM1M2M3 необходимо равенство нулю и главного момента

приложенных сил. При составлении условий равновесия сил приложенных к тетраэдру с использованием главного вектора положение точек приложения поверхностных сил не имело значения, а для определения моментов поверхностных сил необходимо знать координаты точек приложения этих сил. Поскольку грани тетраэдра бесконечно малы, можно принять, что поверхностные силы по ним распределены равномерно и, следовательно, точки приложения равнодействующих сил находятся на пересечении медиан граней тетраэдра в точках N,N1,N2,N3 . Обозначим через r,r(1) ,r(2) ,r(3) радиусы - вектора этих точек. Чтобы не загро-

мождать чертеж, на рис. (4.2) показано положение точек N и N3 и их радиусы вектора. Со-

ставим второе условие равновесия сил приложенных к тетраэдру.

r pn Sn r(1) p1 S1 r(2) p2 S2 r(3) p3 S3.

Заменяя в правой части этого равенства pn его разложением (4.7), получим после сокраще-

ния на Sn

31

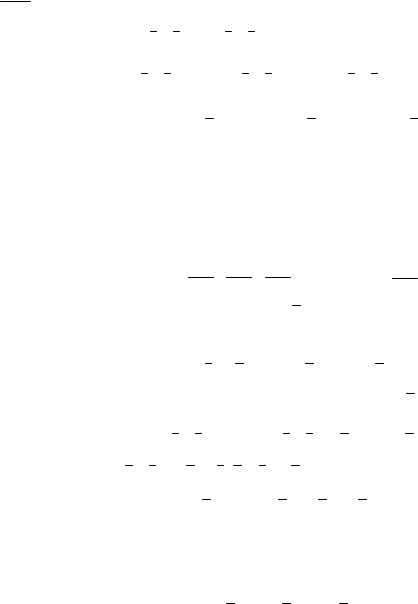
а так как точка N3 является проекцией точки N на плоскость MX1X3 , то направленный отре-

По известной теореме о пересечении медиан в треугольнике будем иметь

'' '

Поскольку концы векторов MN1,MN2,MN3 так же как и MN , лежат в наклонной плоскости M1M2M3 , проекции их на нормаль n к плоскости M1M2M3 будут равны одной и той же величине кратчайшему расстоянию h точки М до плоскости M1M2M3 , так что

Умножая обе части каждого из равенств (4.14) скалярно на n , получим с использованием

(4.16)

Проектируя обе части этого равенства на оси координат и пользуясь известными формулами проекций векторного произведения на те же оси, окончательно получим систему равенств

выражающих теорему о взаимности касательных напряжений: если через какую-нибудь точку среды провести три взаимно перпендикулярные бесконечно малые площадки, то для каждых двух из них проекции вектора напряжения, приложенного к одной из площадок, на нормаль к другой равны между собой.

Из теоремы следует, что из девяти неизвестных компонент тензора напряжений различными являются только шесть.

32

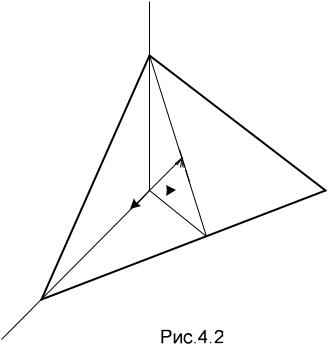
X3

M 3

M1

X1

33

Лекция 5

Уравнения статики сплошной среды “в напряжениях”

Принцип затвердевания, примененный к деформируемому телу, является необходимым, но недостаточным условием равновесия.

Составим еще одно, также только необходимое условие равновесия деформируемого тела, но в отличие от принципа затвердевания, учитывающее действие внутренних сил в сплошной среде.

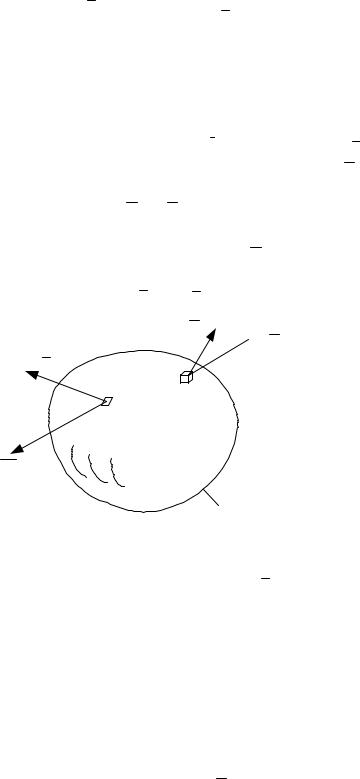
Выделим в сплошной среде произвольный объем (рис.5.1) ограниченный

поверхностью S . К элементарному объему приложена сила F , а к элементарной площади S , ориентированной согласно единичному вектору нормали nˆ к поверхности Sx

сила n S , где n вектор напряжения в точке N поверхности S .

f

nˆ M

N

S

pn S

S

Рис.5.1

Запишем необходимое, согласно принципу затвердевания, условие равновесия равенство нулю главного вектора приложенной к объему и k ограничивающей его поверхности S совокупности сил. Будем иметь

где первый интеграл, взятый по объему , представляет собой главный вектор внешних,

объемных сил f , приложенных к элементам объема , а второй, взятый по поверхности

S , главный вектор внешних поверхностных сил pn S , приложенных к элементам поверхно-

Используя формулу Гаусса – Остроградского, перейдем от поверхностного интеграла к объемному его эквиваленту. Будем иметь

nˆP S DivP ,

S

Пользуясь произволом в выборе объема , применим равенство (5.3) к элементарному объему . Тогда интеграл, стоящий в левой части, сведется к одному слагаемому, получим

( f DivP) 0.

Замечая, что представляет собой произвольную бесконечно малую величину, но не равную нулю, разделим обе части предыдущего равенства на и получим искомое уравнение статики «в напряжениях»:

34

циальных уравнений в частных производных относительно неизвестных компонент тензора напряжений:

И система трех уравнений равновесия заключает в себе не девять, а только шесть неизвестных компонент тензора напряжений, что делает ее недостаточной для определения этих шести неизвестных.

Эту статическую неопределенность можно избежать, вводя дополнительные допущения о физических, свойствах сплошной среды, например о ее упругости, подчиняющейся закону Гука о пропорциональности тензора напряжений тензору деформаций.

Наиболее просто решается вопрос о равновесии идеально текучей среды, в которой касательные напряжения отсутствуют

т.е. для идеальной жидкости три нормальных напряжения, приложенные к трем взаимно перпендикулярным площадкам, как угодно ориентированным в пространстве, равны между собой. Этот закон изотропии нормальных напряжений в точках сплошной среды, находящейся в равновесии, был открыт в середине 17 века Паскалем.

Общее значение нормальных напряжений в данной точке среды, взятое со знаком минус, назовем давлением в этой точке и обозначим р, так что

p11 p22 p33 p. (5.9)

Чтобы подчеркнуть, что принятое определение соответствует лишь случаю равновесия среды, это давление называют гидростатическим давлением.

Знак минус, взятый в определении давления, подчеркивает, что нормальное напряжение

приложенное в точках поверхности мысленно выделенного объема, направлено в сторону, противоположную орту внешней нормали к этой поверхности, т.е. внутрь объема.

Давление p представляет собой физический скаляр, такой же как и плотность, температура, концентрация и др. скалярные характеристики.

При равновесии среды тензор напряжений в ней, согласно (5.6) и (5.9) имеет таблицу

т.е. обладает сферической симметрией, что соответствует свойству изотропии нормальных напряжений в покоящейся среде и можно положить (Е - тензорная единица)

35

эти уравнения носят наименование уравнений Эйлера гидростатики.

Уравнения (5.12 ) легко интегрируются для случая объемной силы тяжести равной f g . Жидкость подверженную силе тяжести называют «тяжелой» жидкостью. В этом случае уравнение (5.12) примет вид

Вэтом заключается известный закон Архимеда: тело, погруженное в жидкость, теряет

всвоем весе столько, сколько весит жидкость в объеме погруженного в нее тела.

Главный вектор Rпов называют архимедовой силой или гидростатической подъемной силой в знак того, что она стремится вытолкнуть тело из окружающей его жидкости.

Легко вычислить также момент сил давления тяжелой жидкости на поверхность погруженного в нее тела. Имеем

Замечая, что по известной формуле векторного исчисления и очевидному тождеству rotr 0

rot(pr) protr gradp r r gradp r g ,

Вводя выражение вектор - радиуса rc центра тяжести вытесненного телом объема жидкости

36

Отсюда следует, что линия действия главного вектора сил давления жидкости на погруженное в нее тело проходит через центр тяжести вытесненного телом объема жидкости.

Из уравнения (5.12) можно исключить плотность и давление. Для этого возьмем сначала от обеих его частей операцию вихря rot; тогда р исключится, так как

rotgradp 0,

будем иметь rot( f ) 0. Отсюда, раскрывая скобки по известному правилу, получим

rot( f ) x ( c f ) x ( fc) ( f ) grad f rotf grad f 0.

Умножая обе части этого равенства скалярно на f , и, замечая, что второе слагаемое, как

векторное произведение, перпендикулярно к своему сомножителю f будет равно нулю, найдем следующее общее ограничение, накладываемое на класс сил, под действием которых возможно равновесие жидкостей и газов:

К числу объемных сил, удовлетворяющих условию (5.19), относятся силы имеющие потенциал П, так как для них

grad gradП 0,

откуда следует, что при равновесии среды силовые линии поля потенциальных, объемных сил ортогональны изостерам (поверхностям одинаковой плотности), а также что изостеры совпадают с изопотенциальными поверхностями силового поля.

Из (5.12) следует, что при равновесии среды силовые линии ортогональны изобарам (поверхностям одинакового давления)

Следовательно, при равновесии жидкости или газа под действием потенциального поля объемных сил изопотенциальные поверхности поля совпадают с изобарами и изостерами.

Если в движущемся или покоящемся газе плотность является функцией только давления, то движение или равновесие газа называют баротропным Из предыдущего следует, что баротропное равновесие среды возможно при наличии только потенциальных сил, так как при условии (p)изобары и изостеры совпадут, а, следовательно, силовое поле должно быть потенциальным. В этом случае уравнения Эйлера (5,12) представляют собой так называемую систему в полных дифференциалах и имеют общее решение вида

где p0 p(M0 ). Чтобы задача была определенной, надо использовать дополнительные до-

пущения о форме и зависимости плотности от давления.

37

Лекция 6

Общие теоремы динамики сплошной среды 1.Теорема об изменении главного вектора количества движения

Напомним формулу этой теоремы в дифференциальном виде

производная по времени от главного вектора количества движения системы равна геометрической сумме всех внешних сил приложенных к системе.

Выделим в движущейся сплошной среде произвольный жидкий объем , ограниченный поверхностью S и применим к нему теорему (рис. 6.1).

Напомним, что в сплошной среде вместо обычных сил вводятся плотности их распределения, соответственно в объемах и на поверхностях: f - для объемных и pn - для поверхно-

стных сил. Если элемент объема, содержащий точку М со скоростью V , то элементарное количество движения этого элемента равно

Q V ,

где - плотность распределения массы в объеме .

Главный вектор количества движения сплошной среды Q , равный векторной сумме элементарных количеств движения будет определяться вычисленным по объему интегралом

(6.1)

F

n

N

S

Pn

Таким образом, применительно к механике сплошных сред, формулировка претерпевает небольшие изменения и становится следующей: индивидуальная производная по времени от главного вектора количества движения «жидкого» объема равна главному вектору внешних объемных и поверхностных сил, приложенных к частицам расположенным в объеме и на ограничивающей его поверхности.

Производная по времени, стоящая слева, следит за всеми изменениями со временем – локальными и конвективными, главного вектора количества движения среды в движущемся вместе со средой объеме . Эту производную можно вычислить по общим правилам дифференцирования интеграла

будет

38

2. Дифференциальные уравнения динамики сплошной среды

Воспользовавшись теоремой об изменении главного вектора количества движения, выведем общее уравнение динамики сплошной среды - так называемое «уравнение в напряжениях». Для этого преобразуем поверхностный интеграл правой части формулы (6.5) в объемный, произведя замену pn n1 p1 n2 p2 n3 p3 и используя формулу Гаусса-Остроградского,

будем иметь эквивалентные друг другу результаты

Подставим в (6.5) приведенные к объемным интегралам члены и объединим их, перенеся в левую часть уравнения

откуда в силу произвольности объема придем к уравнению динамики сплошной среды «в напряжениях»