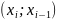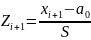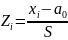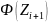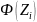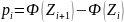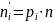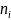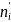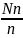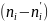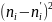Ухтинский Государственный Технический Университет

Кафедра Высшей математики

Домашний типовой расчет

по теме:

«Элементы математической статистики»

Выполнила ст. гр. ГНГ-10 Ларукова А.

Проверила Прудникова О. М.

Ухта 2012

Элементы математической статистики.

1 задача

Выполнение задания

Известны х₁ ,х₂ ,…,х_n – результаты независимых наблюдений над случайной величиной х.

Х – проходка на долото

13 Вариант

31	8	38	133	17	27	33	30	146	163
307	10	28	13	131	63	34	2	11	17
178	11	168	3	12	119	19	12	126	32
179	56	26	82	7	14	73	172	11	166
37	29	39	20	154	10	4	80	59	30
25	37	76	46	25	18	64	26	45	26
15	19	99	5	70	12	8	28	57	136.6
56	31	101	12	16	294

Сгруппируем эти данные в интегральную таблицу

а) Определить объем выборки

n = 76

б) Определить Х_max и X_min элементы выборки

Х_max = 307 X_min = 2

Тогда размах выборки - R = Х_max - X_min =305

в) По формуле Серджеса определяем количество интервалов

k = 1+3,322∙lg(n) = 7,25 ≈ 7

г) Рассмотрим шаг разбиения

h = R÷k = 305÷7 = 43,57

д) Вычислим начальное значение интервальной таблицы

X_нач = X_min -0,5∙h = -19,79

е) Составим интервальную таблицу

где Х – проходка на долото

Xi - …	(-19,79;29,78)	(29,78;67,35)	(67,35;110,92)	(110,92;154,49)	(154,49;198,06)	(198,06;241,63)	(241,63;285,2)	(285,2;328,77)
ni	35	19	7	7	6	0	0	2
Xi ср	4,995	48,565	89,135	132,705	241,63

Построить полигон частот, гистограмму и эмпирическую функцию распределения.

а) Построение полигона частот

Полигоном частот – называют ломанную, отрезки которой соединяют точки (х₁ ,n₁), (х₂ ,n₂), (х_k ,n_k). Для построения полигона на оси абсцисс откладывают варианты х_i , а на оси ординат – соответствующе им частоты n_i . Точки (х_i , n_i) соединяют отрезками прямых и получают полигон частот.

б) Построим гистограмму частот

Гистограммой частот – называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длинною h , а высоты равны отношению n_i /n (плотность частоты).

в) Построить моду и медиану

Модой – называют варианту, которая имеет наибольшую частоту.

Медиана – называют варианту, которая делит вариационный ряд на две части, равные по числу вариант.

Хi	(-19,79;29,78)	(29,78;67,35)	(67,35;110,92)	(110,92;154,49)	(154,49;328,77)
ni	35	19	7	7	8
ni /h	0,8	0,44	0,16	0,16	0,18

г) Найдем и построим эмпирическую функцию распределения

Эмпирической функцией распределения (функцией распределения выборки) – называют функцию F*(x) определяющую частоту события Х<х. F*(x) = n_x /n

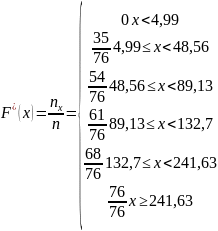
д) Построим кумуляту

Кумулята – это график составленный из накопительных частот то есть это сглаженное изображение эмпирической функции распределения.

Хi	(-19,79;29,78)	(29,78;67,35)	(67,35;110,92)	(110,92;154,49)	(154,49;328,77)
ni	35	19	7	7	8
ni /n	35/76	19/76	7/76	7/76	8/76
Xi ср	4,995	48,565	89,135	132,705	241,63

Найдем несмещенную оценку математического ожидания и дисперсии случайной величины х

Х – проходка на долото

а) Несмещенная оценка

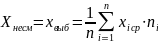
X_несм =

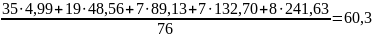
б) исправленная дисперсия

=

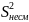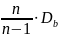
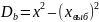
(X_выб)² =363,609

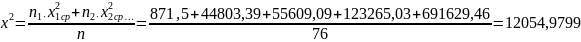
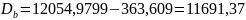
в) «Исправленное» среднее квадратическое отклонение.

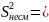
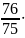11691,37 = 11847,26

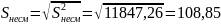
Найти интервальные оценки математического ожидания и дисперсии случайной величины х с надёжностью 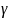= 0,9 и = 0,95

X – проходка на долото; n = 76; X_выб = 60,3; S = 108,85; 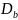= 11691,37; =

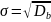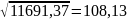
а) Найдем интервальные оценки математического ожидания

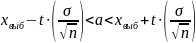
1) Ф(t) = =

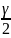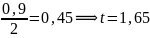
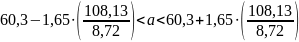
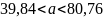
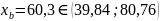
2)

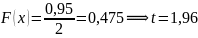
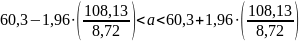
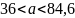
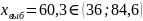
б) Найдем интервальные оценки дисперсии

1) = 0,99; q( ;n) = (0,99;76)

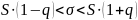
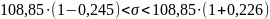
82,18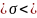 133,45

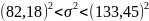
6753,55 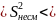17808,9

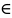(6753,55;17808,9)

2) = 0,95; q( ;n) = (0,95;76)

89,91 126,37

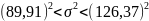
8083,81 15969,38

(8083,81;15969,38)

Выдвинуть гипотезу об истинном значении параметра 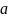нормального распределения и проверить ее при уровне значимости

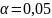
Выдвинем гипотезу об истинном значении параметра нормального распределения и проверим ее при уровне значимости

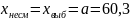
примем

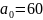
Проверим гипотенузу

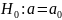
При конкурирующей гипотенузе

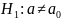
Решение:

а) вычислим наблюдаемое значение критерия

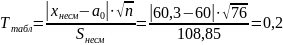
б) при найдем

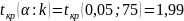
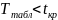
нет основания отвергнуть гипотезу 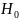,т.е. выборочная средняя 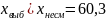незначимо отличается от гипотетической (предполагаемой)генеральной средой

Выдвинуть гипотезу о законе распределения случайной величины x проверить ее по критерию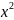 (Пирсона) при уровне значимости

Выведем гипотенузу о нормальном законе распределения случайной величины х и проверим ее по критерию при уровне значимости имеем

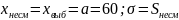
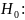нормальный закон распределения наблюдается

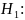нормальный закон распределения не наблюдается

а) Составим вспомогательную таблицу вида

№	Частичный интервал	Нормированный правый конец	Нормированный левый конец			Теоретическая вероятность	Теоретическая частота	Эмпирическая частота
1	(-19,79; 29,78)	-0,28	-0,74	-0,1103	-0,2703	0,16	12,16	35
2	(29,78; 67,35)	0,06	-0,28	0,0239	-0,1103	0,1342	10,2	19
3	(67,35; 110,92)	0,47	0,06	0,1808	0,0239	0,1569	11,92	7
4	(110,92; 154,49)	0,87	0,47	0,3078	0,1808	0,127	9,65	7
5	(154,49; 328,77)	2,47	0,87	0,4932	0,3078	0,1854	14,09	8

б) Сравним эмпирическую и теоретическую частоты.

эмпирическая частота	35	19	7	7	8
теоретическая частота	12,16	10,2	11,92	9,65	14,09

Вывод: расхождение случайно

1	35	12,16	22,84	521,67	42,9
2	19	10,2	8,8	77,44	7,59
3	7	11,92	-4,92	24,21	2,03
4	7	9,65	-2,65	7,02	0,73
5	8	14,09	-6,09	37,09	2,63