Задача 5 Нелинейные модели

Найти оптимальный портфель максимальной эффективности для трех ценных бумаг ЦБ 1, ЦБ 2 и ЦБ 3 с доходностью mi и риском σi, коэффициентами корреляции rij

	ЦБ 1	ЦБ 2	ЦБ 3
mi, %	18	16	7
σi	16	25	16

	ЦБ 1	ЦБ 2	ЦБ 3
ЦБ 1	1	0,16	0,25
ЦБ 2	0,16	1	0,41
ЦБ 3	0,25	0,41	1

Верхняя граница риска задана равной 13.

Решение:

Решение:

Экономико-математическая модель задачи

Оптимальный портфель Марковица максимальной доходности и заданного, (приемлемого) риска r_pможно представить в виде:

1. Подготовим лист для решения задачи, рис.1.

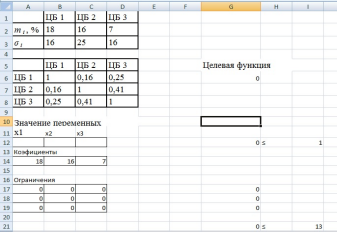
Рис.1.Исходные данные

Таблица 1.Формулы рабочего листа

Адрес ячейки	Формула
G6	=СУММПРОИЗВ(A12:C12;A14:C14)
G12	=СУММ(A12:C12)
G17	=СУММ(A17:C17)
G18	=СУММ(A18:C18)
G19	=СУММ(A19:C19)
G21	=СУММ(G17:G19)
A17	=$A$12*A12*B6
B17	=$B$12*B12*C6
C17	=$C$12*C12*D6
A18	=$A$12*A12*B7
B18	=$B$12*B12*C7

C18 =$C$12*C12*D8

A19 =$A$12*A12*B8

B19 =$B$12*B12*C8

C9 =$C$12*C12*D8

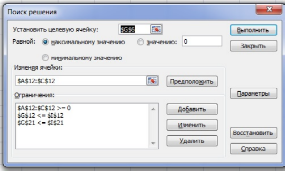
Рис.2. Лист Excelс исходными данными и расчетными формулами для расчета состава оптимального портфеля из трех ценных бумаг

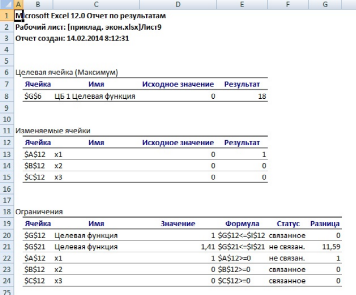
Рис .3. Отчет по результатам

Ответ: оптимальный портфель состоит из ценных бумаг ЦБ1.

Задача 6 Балансовый метод и оптимальное планирование

Задача: Используя балансовый метод планирования и модель Леонтьева построить баланс производства и распределения продукции предприятий.

Промышленная группа предприятий (холдинг) выпускает продукцию трех видов, при этом каждое из трех предприятий группы специализируется на выпуске продукции одного вида: первое предприятие специализируется на выпуске продукции первого вида, второе предприятие – продукции второго вида; третье предприятие – продукции третьего вида. Часть выпускаемой продукции потребляется предприятиями холдинга (идет на внутреннее потребление), остальная часть поставляется за его пределы (внешним потребителям, является конечным продуктом). Специалистами управляющей компании получены экономические оценки aij (i – 1,2,3; j – 1,2,3) технологической матрицы А (норм расхода, коэффициентов прямых материальных затрат) и элементов уjвектора конечной продукции Y.

Требуется:

1. Проверить продуктивность технологической матрицы А = (aij) (матрицы коэффициентов прямых материальных затрат).

2. Построить баланс (заполнить таблицу) производства и распределения продукции предприятий холдинга.

Вариант 15:

Отрасли	Коэффициенты прямых поставок a ij			Конечный продукт Y i
	1	2	3
1 2 3	1А = 0,1 1Б = 0,1 1В = 0,1	2А =0,2 2Б = 0,4 2В =0	3А = 0,2 3Б = 0,2 3В = 0,3	4А = 200 4Б = 140 4В = 180

Решение:

1) Проверить продуктивность технологической матрицы A=(а_ij) (матрицы коэффициентов прямых материальных затрат).

1.1. Для решения данной экономической задачи будет выбрана среда табличного процессора MS Excel. (рис.1)

Рис. 1. Исходные данные

1.2. Найдем разность между единичной матрицей Е и матрицей А.

Для этого воспользуемся правилом вычитания матриц одинаковой размерности. 

Е-А=+(-1)*

	0,9	-0,2	-0,2
E-A	-0,1	0,6	-0,2
	-0,1	0	0,7

1.3. Найдем обратную матрицу . Воспользуемся встроенными функциями MS Excel (математические, обратная матрица) (рис. 2).

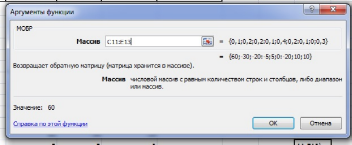
Рис.2.Нахождение обратной матрицы

1.4. Чтобы определить Валовую продукцию  (матрицу), надо матрицу=умножить на Конечный продукт (матрицу). Воспользуемся опять встроенными функциями MS Excel (математические, умножение матриц) (рис. 3.).

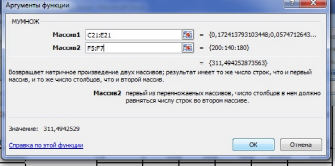
Рис.3.Определение валовой продукции (матрица)

1.5. Матрица (матрица коэффициентов прямых материальных затрат) продуктивна, т.к. существует неотрицательный вектор.

2) Построить баланс (заполнить таблицу)  производства и распределения продукции предприятий холдинга.

2.1. Для распределения продукции предприятий холдинга необходимо найти  

Рис.4. Распределение продукции предприятий холдинга

В результате получили:Таким образом, валовая продукция предприятия

x1 = 4200, x2 =300, x3 =800.

Распределение продукции между предприятиями:

xij = aij·xij

x11 = 0,1 ·380.46= 38.05

x21 = 0,1·380.46=38.05

x31 = 0,1·380.46= 38.05

x12 = 0,2·400.57= 80.11

x22= 0,4*0,2·400.57= 160.11

x32 = 0·0,2·400.57= 0

x13 = 0,2·311.49= 62.30

x23 = 0,2·311.49=62.30

x33 = 0,3·311.49= 93.45

Условно чистая продукция – это разность между валовым продуктом и суммой продуктов, которые потребляет каждая отрасль.

Ответ:

1) Матрица (матрица коэффициентов прямых материальных затрат) продуктивнf.

2)Межотраслевой баланс

Отрасли	Коэффициент прямых поставок aij				Конечный продукт Y		Валовой продукт
	1	2	3
1	38,05	80,11	62,30	200		380,46
2	38,05	160,23	62,30	140		400,57
3	38,05	0,00	93,45	180		311,49
Продукция	114,15	240,3	218,1