
TeorVer / 7. Двухмерные случайные вуличины
.pdf
7. ДВУХМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. КОВАРИАЦИЯ. ФОРМУЛА КОМПОЗИЦИИ
|
Функцией распределения системы двух случайных |
величин |
|||
(X ,Y ) |
называется вероятность совместного выполнения двух нера- |
||||
венств: |
X x, Y |
y |
|
|
|
|
F(x, y) P{X x,Y y} . |
|
|
||
|
Для системы двух дискретных случайных величин (X ,Y ) |
функ- |
|||
ция распределения равна |
|
|
|||
|
F (x, y) |
pij , |
|
|
|
|
|
xi |
x y j y |
|
|
а для системы непрерывных случайных величин: |
|
|
|||
|
|
x |
y |
|
|
|
F (x, y) |
f (z, w)dzdw, |
|
|
|
где |
pij |
– вероятность совместного выполнения равенств |
X |
xi и |
|
Y |
y j |
; f (x, y) |
– совместная плотность распределения системы не- |
||
прерывных случайных величин (X ,Y ) . |
|
|
|||
|
Свойства совместной плотности распределения: |
|
|
||
1.f (x, y) 0 ;
2.f (x, y)dxdy 1 ;
3. f (x, y) |
2 F (x, y) |
; |
|
x y |
|||
|
|
4. вероятность попадания случайной точки (X ,Y ) в некоторую область D равна
61

P{( X ,Y ) D} 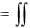 f (x, y)dxdy.
f (x, y)dxdy.
D
Если случайные величины, входящие в систему, независимы, то
F(x, y) FX (x)FY ( y) ,
а для системы непрерывных случайных величин кроме этого f (x, y) 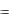 fX (x) fY ( y) .
fX (x) fY ( y) .
Начальным моментом порядка k, s системы двух случайных ве-
личин (X ,Y ) называется |
математическое ожидание |
произведения |
|||||||||||||||
X k |
и Y s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k , s |
M [ X kY s |
] . |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Центральным моментом порядка k, s системы двух случайных |
||||||||||||||||
величин (X ,Y ) |
называется математическое ожидание произведения |
||||||||||||||||
k |
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
и Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
s |
], |
|
|
|
|
|
|
|
|
|||
|
|
k , s |
M [ X |
Y |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
mX |
, |
|
|
|
Y |
mY |
|
– центрированные случайные величи- |
||||||
X X |
|
Y |
|
|
|||||||||||||
ны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Порядок моментов определяется суммой индексов k |
s . |
|||||||||||||||
|
Начальные моменты первого порядка – это математические ожи- |
||||||||||||||||
дания случайных величин X и Y : |
|
|
|
||||||||||||||
1,0 |
M[ X 1Y 0 |
] M [ X ] m |
X |
; |
0,1 |
M[ X 0Y1 ] M[Y ] m . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
||||
Точка (mX , mY ) |
представляет собой характеристику положения слу- |
||||||||||||||||
чайной точки (X ,Y ) , |
и разброс возможных значений |
системы слу- |
|||||||||||||||
чайных величин происходит вокруг этой точки. |
|
||||||||||||||||
|
Центральные |
|
|
моменты |
|
|
первого |
порядка равны нулю: |
|||||||||
1,0 |
|
0,1 |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Центральные моменты второго порядка: |
|
|||||||||||||||
|
|
|
|
2 |
0 |
] |
|
2 |
] |
|
D[ X ] |
DX ; |
|
||||
|
|
2,0 |
M [ X Y |
|
M [ X |
|
|
|
|||||||||
|
|
|
|
0 |
|
2 |
|
|
2 |
] D[Y ] DY ; |
|
||||||
|
|
0,2 |
M[ X Y |
|
] M[Y |
|
|||||||||||
|
|
|
1 1 |
] |
|
M[( X |
|
|
mX )(Y |
mY )] KXY . |
|
||||||
|
|
1,1 |
M[ X Y |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
62 |
|
|
|
|

Первые два центральных момента – это дисперсии случайных величин
X и Y . Момент |
1,1 |
называется смешанным центральным моментом |
|
|
второго порядка или ковариацией (корреляционным моментом) и обычно обозначается как KXY .
Дисперсию можно рассматривать как частный случай ковариа-
ции, т. е.: |
|
|
2 |
|
|
DX M [ X |
] M [ XX ] |
K XX , DY M [YY ] KYY . |
Для независимых случайных величин ковариация всегда равна |
||
нулю. |
|
|
Ковариация характеризует |
степень линейной зависимости слу- |
|
чайных величин и их рассеивание вокруг точки (mX , mY ) . Ее можно выразить через начальные моменты:
KXY 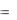 1,1
1,1 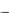 10 01 M[XY ] mX mY .
10 01 M[XY ] mX mY .
Степень зависимости случайных величин X и Y удобнее характеризовать посредством безразмерной величины – коэффициента корреляции:
rXY |
K XY |
|
. |
|
|
|
|
|
|
||
|
X |
Y |
|
|
|
Если rXY |
0 , то говорят, |
что случайные величины X и Y свя- |
|||
заны положительной корреляцией; при rXY |
0 – отрицательная кор- |
||||
реляция между |
случайными |
величинами. |
Диап азон изменения |
||
rXY : 1 rXY 1 .
Математические ожидания и дисперсии случайных величин X и Y , входящих в систему (X ,Y ) , а также ковариация определяются по формулам, представленным в таблице:
|
|
|
|
|
|
Таблица |
|
|
|
|
|
|
|||
|
|
для непрерывных X и Y |
для дискретных X и Y |
|
|||
|
|
|
|
n |
m |
|
|
m |
X |
xf (x, y)dxdy |
mX |
|
|
xi pij |
|
|
|
|
|
|
|
|
|
|
|
|
i |
1 |
j |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
m |
|
|
|
m |
|
yf (x, y)dxdy |
mY |
|
|
y j pij |
|
Y |
|
|
|
|
|
|
|
|
|
|
i |
1 |
j |
1 |
|
|
|
|
|
|
|
|
|
63
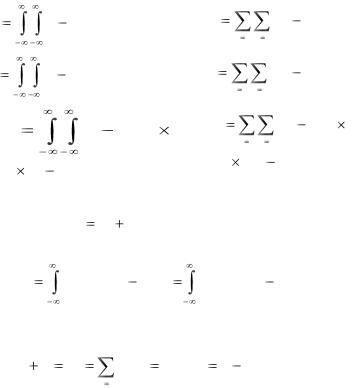
Продолжение таблицы
|
|
для непрерывных X и Y |
для дискретных X и Y |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
n |
m |
|
|
|
|
D |
X |
(x |
m |
X |
)2 f (x, y)dxdy |
DX |
|
|
(xi |
mX )2 pij |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
i |
1 |
j |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
m |
|
|
|
|
|
D |
|
( y |
m )2 f (x, y)dxdy |
DY |
|
|
( y j |
mY )2 pij |
|
||||
|
Y |
|
Y |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
i |
1 |
j |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
m |
|
|
|
K XY |
|
(x |
mX ) |
K XY |
|
|
(xi |
mX ) |
|
||||
|
|
|
i |
1 j 1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
( y mY ) f (x, y)dxdy |
|
( y j |
mY ) pij |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||||||
|
|
Плотность распределения |
fZ (z) |
суммы двух независимых слу- |
||||||||||
чайных |
величин |
Z |
|
X |
Y |
вычисляется по |
формуле композиции |
|||||||
(свертки) плотностей |
fX (x) и |
fY ( y) в виде |
|
|
|
|
|
|||||||
|
|
fZ (z) |
f X (x) fY (z x)dx |
fY ( y) f X (z y)dy . |
||||||||||
Для независимых дискретных случайных величин X и Y существует следующая формула композиции
n |
|
P{X Y n} |
P{X k}P{Y n k}. |
k |
0 |
ЗАДАЧИ ДЛЯ АУДИТОРНЫХ ЗАНЯТИЙ
7.1. Бросают две игральные кости. Пусть X – сумма очков, выпадающих на верхних гранях. Написать закон распределения случайной величины X.
Ответ:
xi |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
pi |
1/36 |
2/36 |
3/36 |
4/36 |
5/36 |
6/36 |
5/36 |
4/36 |
3/36 |
2/36 |
1/36 |
|
|
|
|
|
|
|
|
|
|
|
|
64
7.2. Законы распределения числа очков, выбиваемых каждым из двух стрелков, таковы:
xi |
1 |
2 |
3 |
|
|
|
|
pi |
0,1 |
0,3 |
0,6 |
|
|
|
|
yi |
1 |
2 |
3 |
|
|
|
|
pi |
0,2 |
0,3 |
0,5 |
|
|
|
|
Найти закон распределения суммы очков, выбиваемых двумя стрелками.
Ответ:
сумма очков |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
вероятность |
0,02 |
0,09 |
0,26 |
0,33 |
0,30 |
|
|
|
|
|
|
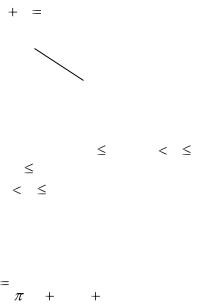
7.3. По мишени производится один выстрел. Вероятность попадания равна p. Рассматриваются две случайные величины: X – число попаданий; Y – число промахов. Построить функцию распределения F(x, y) двумерной случайной величины (X ,Y ) .
Ответ:
Случайные величины X, Y зависимы, причем жестко (функционально), p q 1 . Таблица возможных значений X,Y с соответствующими вероятностями имеет вид
|
Y |
0 |
1 |
X |
|
||
|
|
|
|
0 |
|
0 |
q |
1 |
|
p |
0 |
Значения функции F(x, y) приведены в следующей таблице:
|
|
x |
0 |
0 x 1 |
x>1 |
y |
0 |
|
0 |
0 |
0 |
|
|
|
|
|
|
0 |
y 1 |
|
0 |
0 |
p |
|
|
|
|
|
|
y>1 |
|
0 |
q |
1 |
|
7.4. Двумерная случайная величина (X ,Y ) имеет плотность ве-
роятности |
|
|
f (x, y) |
A |
|
|
. |
|
2 (3 x2 )(1 y2 ) |
||
65
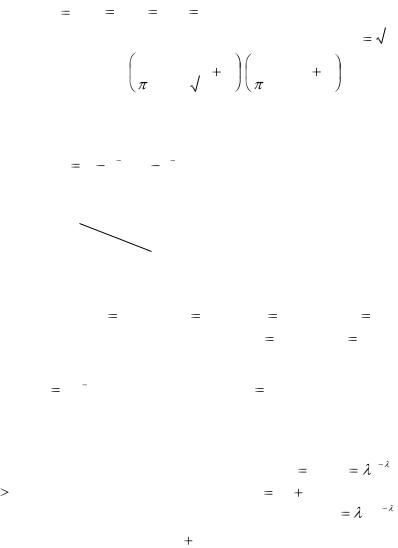
Найти: а) величину A; б) функцию распределения F(x, y) ; в) вероят-
ность попадания случайной точки |
|
(X ,Y ) |
в квадрат, |
ограниченный |
||||||||||||||
прямыми x 0 , y 0 , |
x 1, y |
1. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: а) |
3 ; |
|||||
б) F(x, y) = |
1 |
arctg |
|
x |
|
1 |
|
|
1 |
arctgy |
|
1 |
|
; в) 0,0417 |
||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|||||||
|
3 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7.5. Определить плотность вероятности системы двух положи-
тельных случайных величин X и Y по заданной функции распределения
F (x, y) (1 e ax )(1 e by ) .
7.6. Случайная точка |
(X ,Y ) |
на плоскости распределена по сле- |
||||||
дующему закону: |
|
|
|
|
|
|
|
|
|
|
Y |
|
–1 |
0 |
1 |
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0,1 |
0,15 |
0,20 |
|
|
|
1 |
|
|
0,15 |
0,25 |
0,15 |
|
|
|
Найти числовые характеристики (X ,Y ) . |
|
|
|
|||||
Ответ: M[X ] |
0,55; M[Y] |
0,1; D[X ] 0,2475; D[Y ] |
0,59; |
|||||
|
|
|
|
|
K XY |
– 0,055; rXY |
– 0,144 |
|
7.7. Пусть заданы случайная величина X с плотностью вероятно- |
||||||||
сти f (x) Ae x 2 |
и случайная величина Y |
X 2 . Показать, что для |
||||||
этих явно зависимых случайных величин коэффициент корреляции равен нулю.
7.8. Случайные величины X и Y независимы и имеют одно и то же
показательное распределение с плотностью |
f X (x) |
fY (x) |
e |
x , |
x 0. Найти плотность случайной величины Z |
X |
Y . |
|
|
Ответ: |
fZ (x) |
2 xe |
x |
|
7.9. Доказать, что сумма X Y независимых нормально распределенных случайных величин X и Y с параметрами соответственно
66

( m1, 1 ) |
и ( m2 , |
2 ) |
|
нормально |
распределена |
с |
параметрами |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
m |
m , |
|
|
|
2 |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
2 |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.10. Случайные величины распределены по закону Пуассона: |
|
|||||||||||||||||||||||
|
|
|
|
k |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
P{X k} |
|
|
e |
1 , P{Y m} |
|
|
e 2 . |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
k! |
|
|
|
|
|
m! |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Найти закон распределения их суммы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
1 |
|
2 )n |
|
( |
1 |
2 ) |
|||
|
|
|
|
|
|
|
Ответ: P{X |
Y |
n} |
|
|
|
|
|
|
e |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
7.11. Найти функцию распределения суммы независимых случай- |
||||||||||||||||||||||||
ных величин X и Y, первая из которых равномерно распределена на |
|||||||||||||||||||||||||
интервале [ h; h] , а вторая имеет функцию распределения F(y) . |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
h |
|
|
|
|
|
|
|
|
Ответ: F(z) |
P{X |
Y |
z} |
|
|
F (z |
|
x)dx |
|||||||||||||||
|
|
2h |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
||
|
7.12. Случайные величины X и Y независимы и имеют равномер- |
||||||||||||||||||||||||
ное |
распределение |
на |
отрезке |
[0; |
1]: |
f (x) |
1 |
при |
0 |
|
|
x |
1 |
и |
|||||||||||
f ( y) 1 при 0 |
y |
1 . Найти функцию распределения и плотность |
|||||||||||||||||||||||
вероятности случайной |
величины |
Z |
X |
Y . |
|
Построить |
|
график |
|||||||||||||||||
функции |
f (z) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
z |
0; |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Ответ: f (z) |
|
|
z, |
0 |
z |
|
1; |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
z, |
1 |
|
z |
|
2; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
z |
2 |
|
|
|
|
|
7.13. Найти математическое ожидание и дисперсию произведения независимых случайных величин X и Y с равномерными законами распределения: X – на интервале [0; 1], Y – [1; 3].
Ответ: 1, 4/9
67
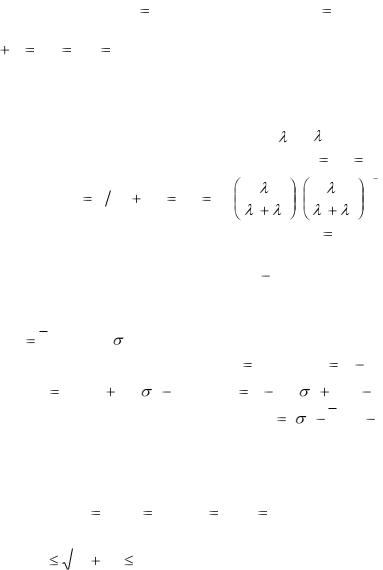
7.14. Случайная величина |
(X ,Y ) |
подчинена закону распределе- |
|||||||||||||||
ния с плотностью |
f (x,y) |
|
Axy в области D и |
f (x, y) |
0 вне этой |
||||||||||||
области. |
Область |
D |
|
– |
|
треугольник, |
ограниченный |
прямыми |
|||||||||
x y |
1, x 0, y |
0. Найти: а) величину A; |
б) M[X ] и M[Y ] ; |
||||||||||||||
в) D[ X ] и D[Y] ; г) KXY ; д) rXY . |
|
|
|
|
|
|
|
|
|||||||||
|
Ответ: а) 24; б) 2/5, 2/5; в) 0,2475, 0,2475; г) –2/75; д) –2/3 |
||||||||||||||||
7.15. Пусть случайные величины |
X1 и |
X 2 |
независимы и подчи- |
||||||||||||||
няются распределению Пуассона с параметрами |
1 и |
2 . Найти ус- |
|||||||||||||||
ловное распределение |
X1 |
при фиксированной сумме X1 |
X 2 N . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
N k |
|
Ответ: P{X |
|
k X |
|
|
X |
|
N} |
C k |
1 |
|
|
|
2 |
|
, |
||
1 |
1 |
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0, 1, ..., N |
||||
7.16. В триоде катод излучает n электронов. С вероятностью p |
|||||||||||||||||
электрон попадает на анод, |
и с вероятностью 1 |
p электрон попадает |
|||||||||||||||
на сетку. Найти математическое ожидание и дисперсию числа электронов, попавших на анод na и на сетку nc и Kna ,nc . Известны
M[n] n и D[n] 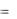 2 .
2 .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: M [na ] pn , M [nc ] |
|
(1 p)n , |
||||||
|
|
|
|
|
|
|
|||||
D[n ] M[n ] |
p2 ( |
2 n) , D[n ] (1 p)2 2 |
np(1 p) , |
||||||||
a |
a |
|
|
|
c |
|
|
|
|
||
Kna ,nc ( 2 n) p(1 p)
ЗАДАЧИ ДЛЯ ДОМАШНИХ ЗАДАНИЙ И САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
7.17. Случайные величины X,Y независимы и нормально распре-
делены с M[X ] |
M[Y ] 0, D[X ] D[Y ] |
1. Найти вероятность |
|||
того, что |
случайная |
точка (X ,Y ) |
попадет в кольцо |
||
|
|
|
|
|
|
{(x, y) : 2 |
x2 |
y2 |
3}. |
|
|
|
|
|
|
|
Ответ: 0,1242 |
68

7.18. Ведется стрельба по мишеням. Найти корреляционный мо-
мент числа попаданий в девятку и в восьмерку при n выстрелах, если вероятность при каждом выстреле выбить 1, 2, ..., 10 очков одинакова.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: r n /100 |
||||||||||
|
7.19. |
Найти |
плотность вероятности модуля радиуса-вектора |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
R |
|
X 2 |
Y 2 , |
если случайные величины X и Y независимы и рас- |
||||||||||||||||||||||||||
пределены |
по |
нормальному |
закону |
|
|
с |
|
|
M[X ] |
|
|
M[Y ] |
0 , |
|||||||||||||||||
D[ X ] |
D[Y ] |
|
|
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Ответ: f (r) |
|
r |
|
e r 2 / 2 2 , r |
|
0; 0, r |
0 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.20. Независимые случайные величины X и Y распределены нор- |
|||||||||||||||||||||||||||||
мально, |
M[X ] |
2 , |
M[Y] |
3 , |
D[X ] |
|
4 , |
|
D[Y] |
9 . Написать |
||||||||||||||||||||
плотность вероятности и функцию распределения их суммы. |
|
|
|
|||||||||||||||||||||||||||
|
7.21. Пусть n – число инжектированных электронов из эммитора в |
|||||||||||||||||||||||||||||
базу, |
из |
них |
nb |
– |
рекомбинировало и |
nk |
– |
попало |
в коллектор |
|||||||||||||||||||||
(n |
nb |
|
nk ) . Известны: p – вероятность пролета электрона через |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
D[n] |
2 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||
базу; |
|
M[n] |
n |
и |
Найти |
M [n ] , M [n ] , D[n ] , |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
k |
b |
||||||
D[nk ] , Knb ,nk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Ответ: M [nb ] (1 |
|
p)n , M [nk ] |
pn , |
|||||||||||||||||
|
|
D[n ] (1 p)2 2 |
|
p2 2 |
|
|
|
|
|
|||||||||||||||||||||
|
|
np(1 p) , D[n ] |
|
np(1 p) , |
||||||||||||||||||||||||||
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Kn |
|
|
( 2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,n |
k |
n) p(1 p) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
7.22. Случайные величины X и Y независимы и нормальны с одинаковыми параметрами m и . а) Найти коэффициент корреляции
величин Z1 aX |
bY и Z2 aX bY . б). Доказать, |
что |
||||
M[max( X ,Y )] m |
/ |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Ответ: а) r |
, z |
a2 |
b2 |
|
|
|
z |
2 |
|
|
|
1 |
|
|
|||
69
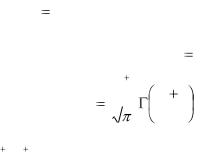
7.23. Найти |
KX , X k |
, k 1, 2, ... , если X – случайная величина, |
||||||||||
распределенная по нормальному закону с параметрами (0,1). |
||||||||||||
|
|
Ответ: K X , X k |
|
|
0 для четных k; |
|||||||
|
|
|
|
k |
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
k |
1 |
|
||||
|
|
K X , X k |
|
|
|
|
|
|
|
|
для нечетных k |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
7.24. Найти |
KX Z ,Z |
Y , если X,Y,Z – независимые случайные ве- |
||||||||||
личины с заданными дисперсиями. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: D[Z] |
