
TeorVer / 5. Формула Бернулли
.pdf
5. ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ ИСПЫТАНИЙ И ФОРМУЛА БЕРНУЛЛИ. ТЕОРЕМЫ МУАВРА – ЛАПЛАСА.
ФОРМУЛА ПУАССОНА
Если производится n независимых опытов, в каждом из которых событие А может появиться с вероятностью p , то вероятность того, что событие А появится ровно m раз (формула Бернулли):
P |
Cm pmqn m , |
q 1 p . |
|
m,n |
n |
|
|
Теоремы Муавра – Лапласа применяются для приближенного вы- |
|||
числения вероятностей |
|
|
|
|
Cm pmqn m , |
b |
|
P |
и P{a m b} |
P |
|
m,n |
n |
|
m,n |
|
|
m |
a |
в n независимых испытаниях при больших n , |
m , a и b . |
||
Локальная теорема Муавра-Лапласа. Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и
равна |
p (0 |
|
p 1) , |
то вероятность Pm,n |
того, что в этих испытаниях |
||||||||||||
событие А наступит ровно m раз, удовлетворяет при n |
соотно- |
||||||||||||||||
шению |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P |
1 |
|
|
|
|
|
|
m |
np |
|
, |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
m,n |
|
|
npq |
|
|
|
|
npq |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
где |
(x) |
|
1 |
|
e |
x |
2 |
2 . Таблица функции |
(x) приведена в прило- |
||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
жении 1. Функция |
(x) – четная: ( x) |
(x) . |
|
||||||||||||||
Интегральная теорема Муавра – Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность собы-
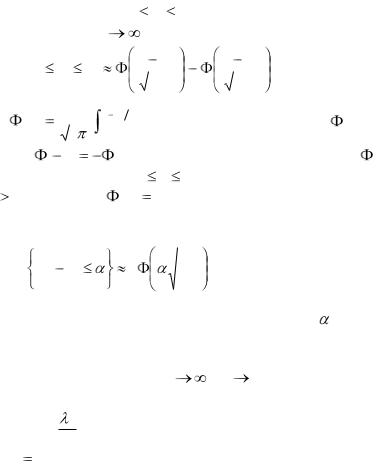
тия А равна |
p , причем 0 |
p |
1 , число успехов m находится между |
|||||||||||||||||||||
a и b , равна при n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
P{a m b} |
|
|
|
|
b np |
|
|
|
|
a |
np |
|
, |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
npq |
|
|
|
|
|
npq |
|
|||
|
|
|
|
1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
(x) |
|
|
|
e |
z |
2 |
2dz – функция Лапласа. Функция (x) |
– не- |
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
2 |
|
0 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
четная: |
( |
x) |
|
|
|
(x) . Таблица значений функции Лапласа |
(x) |
|||||||||||||||||
для положительных |
x |
(0 |
x |
5) |
|
приведена в приложении 2; для |
||||||||||||||||||
x |
5 полагают, что |
|
(x) 0,5 . |
|
|
|
|
|
|
|
|
|
||||||||||||
|
При использовании интегральной теоремы Муавра – Лапласа |
|||||||||||||||||||||||
можно получить формулу |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
P |
m |
|
p |
|
|
|
|
|
|
2 |
|
|
|
n |
, |
|
|
|
|
|
|||
|
n |
|
|
|
|
|
|
|
|
pq |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
которая позволяет найти вероятность того, что частота наступления со-
бытия А отклонится от вероятности |
p не более чем на , если про- |
||
водится n независимых испытаний, |
в каждом из которых вероятность |
||
наступления события А равна |
p . |
|
|
Теорема Пуассона. Если |
n |
, p |
0 , то вероятность ровно |
m положительных исходов при n испытаниях равна
m
Pm,n 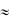 m! e
m! e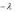 ,
,
где  np .
np .
ЗАДАЧИ ДЛЯ АУДИТОРНЫХ ЗАНЯТИЙ
5.1. Игральная кость брошена 10 раз. Найти вероятность выпадения единицы 7 раз.
Ответ: 0,0002481
5.2. Имеется 5 станций, с которыми поддерживается связь. Время от времени связь прерывается из-за атмосферных помех. Вследствие удаленности станций друг от друга перерыв связи с каждой из них про-
исходит независимо от остальных с вероятностью 0,2. Найти вероятность того, что в данный момент времени будет иметься связь не более чем с двумя станциями.
Ответ: 0,05792
5.3. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен): три партии из четырех или пять партий из восьми?
Ответ: вероятнее выиграть три из четырех
5.4. Наблюдениями установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность, что из случайно взятых в этом месяце 8 дней 3 дня окажутся дождливыми?
Ответ: 0,2787
5.5. Прибор состоит из 8 однородных элементов, но может работать при наличии в исправном состоянии не менее 7 из них. Каждый из элементов за время работы прибора t выходит из строя независимо от других с вероятностью 0,2. Найти вероятность того, что прибор откажет за время t.
Ответ: 0,497
5.6. Система радиолокационных станций ведет наблюдение за группой из 10 объектов. Каждый объект может быть (независимо от других) потерян с вероятностью 0,1. Найти вероятность того, что хотя бы один объект будет потерян.
Ответ: 0,65
5.7. Изделия некоторого производства содержат 5 % брака. Найти вероятность того, что среди пяти взятых наугад изделий: а) нет ни одного испорченного; б) будут два испорченных.
Ответ: а) 0,77; б) 0,02
5.8. По каналу связи передаются n 6 сообщений, каждое из которых независимо от других с вероятностью p 0,2 оказывается ис-
каженным. Найти вероятность следующих событий: A={ровно два сообщения из 6 искажены}; B={не менее двух сообщений из 6 искажены}; C={все сообщения переданы без искажений}; D={все сообщения искажены}.
Ответ: P(A) 0,24576 ; P(B) 0,345 ; P(C) 0,262 ; P(D) 0,000064
5.9.Вероятность рождения мальчика равна 0,515, девочки – 0,485.
Внекоторой семье шестеро детей. Найти вероятность того, что среди них не больше двух девочек.
Ответ: 0,3723
5.10. Пару игральных костей бросают 8 раз. Найти: а) вероятность выпадения 7 очков ровно 4 раза; б) вероятность выпадения 11 очков в двух испытаниях; в) вероятность того, что сумма 12 очков выпадет более одного раза.
Ответ: а) 0,026; б) 0,0613; в) 0,0193
5.11. Вероятность получения удачного результата при производстве сложного химического опыта равна 2/3. Найти наивероятнейшее число удачных опытов, если общее их количество равно 7.
Ответ: 5
5.12. Вероятность попадания в цель при каждом выстреле из орудия равна 0,8. Сколько нужно произвести выстрелов, чтобы наивероятнейшее число попаданий было равно 20?
Ответ: 24 или 25
5.13. В первые классы принято 200 детей. Определить вероятность того, что среди них окажется 100 девочек, если вероятность рождения мальчика равна 0,515.
Ответ: 0,051
5.14. Вероятность появления успеха в каждом испытании равна 0,25. Какова вероятность, что при 300 испытаниях успех наст у- пит: а) ровно 75 раз? б) ровно 85 раз?
Ответ: а) 0,0532; б) 0,0219
5.15. Какова вероятность того, что в столбике из 100 наугад отобранных монет число монет, расположенных "гербом" вверх, будет от
45 до 55?
Ответ: 0,6826
5.16. (Парадокс "гербов" и "решек".) При игре в "гербы" и "решки" бросили монету 100 раз. Подсчитать вероятности следующих событий: а) A={выпало ровно 50 "гербов"}; б) B={выпало, по крайней мере, 60 "гербов"}; в) C={выпало, по крайней мере, 55 "гербов"}.

Ответ: P(A) 0,08 ; P(B) 0,023 ; P(C) 0,16
5.17. Вероятность появления успеха в каждом из 625 независимых опытов равна 0,8. Найти вероятность того, что частота появления успеха отклонится по абсолютной величине от его вероятности не более чем на 0,04.
Ответ: 0,9876
5.18. Сколько нужно произвести опытов с бросанием монеты, чтобы с вероятностью 0,92 можно было ожидать отклонение частоты выпадения "герба" от теоретической вероятности 0,5 на абсолютную величину, меньшую, чем 0,01?
Ответ: n 7656
5.19. В лотерее из 40000 билетов ценные выигрыши падают на 3 билета. а) Определить вероятность получения хотя бы одного выигрыша на 1000 билетов. б) Сколько нужно приобрести билетов, чтобы вероятность получения ценного выигрыша была не менее 0,5?
Ответ: а)1 C1000 |
/ C1000 .; б) 1001 |
39997 |
40000 |
5.20. Вероятность появления успеха в каждом из 400 независимых |
|
испытаний равна 0,8. Найти такое положительное |
, что с вероятно- |
стью 0,9876 абсолютная величина отклонения частоты появления успеха от его вероятности 0,8 не превысит .
Ответ: 0,05
5.21. Известно, что вероятность рождения мальчика приблизительно равна 0,515. Какова вероятность того, что среди 10 тысяч новорожденных мальчиков будет не больше чем девочек?
Ответ: 0,0013
5.22. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двух и более пуль, если число выстрелов равно 5000.
Ответ: 0,9596
5.23. Изготовитель радиоэлектронного оборудования закупает 1000 интегральных микросхем, каждая из которых с вероятностью 0,01 может оказаться неисправной. Какова вероятность того, что: а) неис-
правны будут ровно 10 микросхем; б) все микросхемы окажутся неисправными; в) из всех микросхем неисправна будет лишь одна.
Ответ: а) 0,1251 ; б) 4,32  10 5 ; в) 0,0005
10 5 ; в) 0,0005
5.24. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0,004. Найти вероятность того, что в течение одной минуты обрыв произойдет на пяти веретенах.
Ответ: 0,1563
5.25. Аппаратура состоит из 1000 элементов, каждый из которых независимо от остальных выходит из строя за время T с вероятностью 5 104. Найти вероятность следующих событий: A={за время T откажет ровно 3 элемента}; B={откажет хотя бы один элемент}.
Ответ: 0,013; 0,394
5.26. Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0,01. Телефонная станция обслуживает 800 абонентов. Какова вероятность, что в течение часа позвонит 5 абонентов?
Ответ: 0,0916
5.27. Имеется общество из 500 человек. Найти вероятность того, что у двух человек день рождения придется на Новый год. Считать, что вероятность рождения в любой день равна 1/365.
Ответ: 0,2385
5.28. Вероятность того, что микросхема не выдержит испытания, равна 0,0004. Найти вероятность того, что из 7000 микросхем не менее двух не выдержат испытаний.
Ответ: 0,908
ЗАДАЧИ ДЛЯ ДОМАШНИХ ЗАДАНИЙ И САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
5.29. Устройство состоит из 8 независимо работающих элементов. Вероятности отказов каждого из элементов за время T одинаковы и равны p 0,2 . Найти вероятность отказа прибора, если для этого достаточно, чтобы отказали 3 элемента из восьми.

Ответ: 0,203
5.30. Пусть вероятность попадания в цель при одном выстреле равна p, а вероятность поражения цели при k 1 вы стр ел ах по ней 1 qk . Какова вероятность того, что цель поражена, если произведено n выстрелов?
Ответ: 1 (1 p pq)n
5.31. Кодирование сообщений в цифровой системе связи выполняется путем преобразования в последовательность двоичных чисел 0 и 1. Воздействие шума приводит к ошибочному приему. Вероятность передачи нуля составляет 0,4, а единицы 0,6. Кроме этого вероятность приема 1 при передаче 0 равна 0,08, а вероятность приема 0 при передаче 1 равна 0,05. Определить вероятность того, что при приеме шести символов: а) не будет допущено ни одной ошибки; б) будет допущена ровно одна ошибка; в) будет допущено более одной ошибки; г) возникнет одна или большее число ошибок.
Ответ: а) 0,6811; б) 0,2701; в) 0,04877; г) 0,3189
5.32. Проводятся испытания по схеме Бернулли с вероятностью успеха в одном испытании p 0 . Какова вероятность того, что для
достижения n успехов потребуется n |
k испытаний, k |
0, 1, ? |
|
|
||||||||
Ответ: Полученное распределение называется отрицательно би- |
||||||||||||
|
|
|
|
номинальным с параметрами p и n |
2, . |
|||||||
P(n, n k) Cn 1 |
k |
pnqk |
Ck |
pn ( q)k , q 1 p, |
k |
0,1, , |
||||||
|
n 1 |
|
|
|
n |
|
|
|
|
|
|
|
где |
Ck |
|
|
|
( n)( n |
1)...( n k 1) |
( 1)k Ck |
|
; |
|||
|
|
|
|
|
|
|
1 |
|||||
|
n |
|
|
|
|
|
k! |
|
n k |
|
||
|
|
|
|
|
|
|
|
|
|
|
||
при n 1: |
P(1,k |
1) |
pqk – геометрическое распределение |
|||||||||
5.33. При передаче сообщения вероятность искажения одного знака равна 0,1. Найти вероятность, что сообщение из 10 знаков: а) не будет искажено; б) содержит 3 искажения; в) содержит не более трех искажений.
Ответ: а) 0,3487; б) 0,0534; в) 0,9872
5.34. (Задача Банаха.) Некий курящий математик носит с собой две коробки спичек. Каждый раз, когда он хочет достать спичку, он наугад выбирает одну из коробок. Найти вероятность того, что когда математик вынет в первый раз пустую коробку, в другой коробке ока-
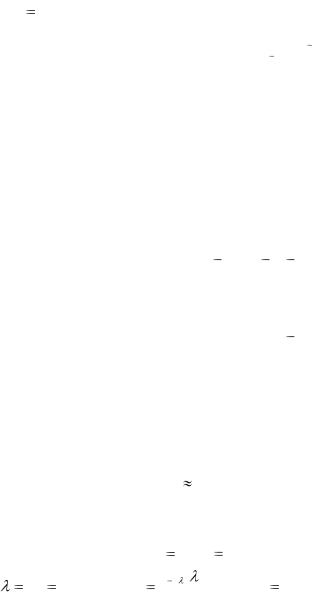
жутся r спичек ( r 0, 1, 2, ...n; n – число спичек, бывших первоначально в каждой из коробок).
Ответ: C2nn r  22n r
22n r
5.35. Два равносильных шахматиста договорились сыграть матч из 2n результативных партий (ничьи не учитываются). Выигравшим матч считается тот, кто победит в большем числе партий. В каком матче больше шансов выиграть — в матче из 8 результативных партий или из 12?
Ответ: из 12 партий
5.36. Стрельба ведется до первого попадания. Выстрелы независимы и вероятность попадания при каждом выстреле равна p. Какова вероятность того, что потребуется 6 выстрелов, если известно, что было сделано четное число выстрелов?
Ответ: (1 p)4 (1 (1 p)2
5.37. Ведется стрельба до первого попадания. Выстрелы независимы с вероятностью попадания, равной p. Какова вероятность того, что первые два выстрела неудачны?
Ответ: (1 p)2
5.38. Для лица, дожившего до 20-летнего возраста, вероятность смерти на 21-м году жизни равна 0,006. Застрахована группа в 10000 человек 20-летнего возраста, причем каждый застрахованный внес по 1,2 рубля страховых взносов за год. В случае смерти застрахованного страховое общество выплачивает наследникам 100 рублей. Какова вероятность того, что: а) к концу года страховое учреждение окажется в убытке; б) его доход превысит 6000 рублей; в) доход превысит 4000 рублей?
Ответ: а) 0,0000; б) 0,5; в) 0,995
5.39. На лекции присутствует 200 человек. Найти вероятность того, что k человек из присутствующих родились 1 января, а m родились 1 мая. Считать, что вероятность рождения в фиксированный день рав-
на 1/365. Вычислить эту вероятность при k |
1 и m |
2 . |
||
|
|
|
k+m |
|
Ответ: |
np 0,548 , p(k,m) e |
2 |
|
, p(1,2) 0,0275 |
|
k!m! |
|||
|
|
|
|
|

5.40. Из одной ЭВМ на другую необходимо передать файл объемом 8000 символов. Вероятность ошибки при передаче символа составляет 0,001. Определить: а) вероятность безошибочной передачи файла; б) вероятность того, что будет ровно 10 ошибок; в) какова должна быть вероятность ошибки при передаче символа, чтобы вероятность передачи всего файла без ошибок составила 0,99?
Ответ: а) 0,000334; б) 0,0993 ; в) 1,256  10 6
10 6
5.41. Предположим, что при наборе существует вероятность p 0,0001 того, что любая буква будет набрана неправильно. После
набора гранки прочитывает корректор, который обнаруживает каждую опечатку с вероятностью q 0,9 . После корректора – автор, обнару-
живающий каждую из оставшихся опечаток с вероятностью r 0,5 . Найти вероятность того, что в книге, имеющей 100000 печатных знаков, останется после этого не более 10 незамеченных опечаток.
Ответ: 1
5.42. Для того, чтобы узнать, сколько рыб в озере, отлавливают 1000 рыб, метят и выпускают обратно в озеро. При каком числе рыб в озере вероятность встретить среди пойманных 150 рыб 10 меченых будет наибольшей?
Ответ: 15000
5.43. (Парадокс дня рождения.) Если собираются вместе ровно 365 человек, то возможно, что все они имеют разные дни рождения. (Не рассматриваем високосный год.) Однако среди 366 человек наверняка (100 %) найдутся, по крайней мере, два таких, у которых дни рождения приходятся на один и тот же день. Определить, сколько должно быть людей, чтобы с вероятностью: а) 99 %; б) 99,9 %, по крайней мере, два человека имели одинаковый день рождения.
Ответ: а) 58; б) 71
5.44. Книга в 500 страниц содержит 50 опечаток. Оценить вероятность того, что на случайно выбранной странице не менее 3 опечаток.
Ответ: 0,000155
