TeorVer / 6. Законы распределения
.pdf
6. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ И ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Под случайной величиной понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение. Случайная величина считается заданной, если известен ее закон распределения, который может принимать различные формы.
Наиболее общей формой закона распределения, пригодной как для дискретных, так и недискретных случайных величин является функция распределения.
Функцией распределения случайной величины Х называется вероятность того, что она примет значение меньшее, чем заданное х (аргумент функции)
F(x) P{X x}.
|
Свойства функции распределения: |
||||
1. |
0 F(x) |
1 – функция распределения F(x) является неотрица- |
|||
тельной, заключенной между нулем и единицей; |
|||||
2. |
F (x1) |
F(x2 ) , если x1 |
x2 – функция распределения F(x) яв- |
||
ляется неубывающей; |
|
||||
3. |
F( |
) 0, F( |
) 1; |
|
|
4. |
P{a |
X |
b} |
F(b) |
F(a) – вероятность попадания случайной |
величины Х на интервал [a,b) .
Если Х – дискретная случайная величина, принимающая значения x1, x2 , с вероятностями p1 , p2 , , то ее функция распределения равна
F (x) P{X x} |
pi . |
xi |
x |
|
40 |
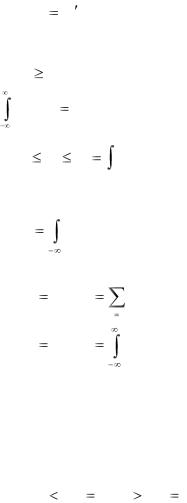
Плотностью распределения вероятностей f (x) непрерывной
случайной величины Х называется первая производная от ее функции распределения, т.е.
f (x) F (x) .
График функции f (x) называется кривой распределения. Свойства плотности распределения:
1. f (x) 0 – плотность распределения неотрицательна;
2.f (x)dx 1 – площадь под кривой распределения равна 1;
|
b |
|
3. P{a |
X b} |
f (x)dx – вероятность того, что непрерывная |
|
a |
|
случайная величина X принадлежит интервалу [a,b] ; |
||
|
x |
|
4. F (x) |
f (z)dz . |
|
Математическим ожиданием случайной величины X называют: |
||
|
|
n |
mX |
M [ X ] |
xi pi для дискретной случайной величины; |
|
i |
1 |
mX |
M [ X ] |
xf (x)dx для непрерывной случайной ве- |
личины.
Модой дискретной случайной величины называется ее наиболее вероятное значение. Модой непрерывной случайной величины называ-
ется то ее значение, при котором функция f (x) достигает максимума. Медианой непрерывной случайной величины X называется та-
кое ее значение xm , для которого
P{X xm } P{X xm } 1
2 ,
т.е. одинаково вероятно, окажется ли случайная величина X меньше xm или больше xm .
41
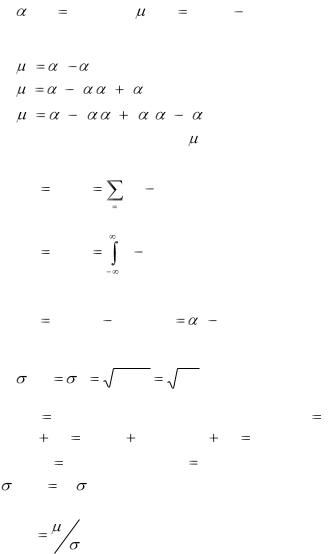
Начальные и центральные моменты s -го порядка случайной величины X определяются соответственно формулами:
s |
[X ] M[X s ] |
и |
s |
[ X ] M[( X m )s ]. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
X |
|||
Центральные моменты выражаются через начальные следующим |
|||||||||||||||
образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
2 |
12 ; |
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
3 |
3 |
1 |
2 |
2 |
13 ; |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
4 |
4 |
4 |
1 |
3 |
6 |
1 |
|
2 |
|
3 |
1 . |
||||
Второй центральный момент |
2[ X ] называется дисперсией слу- |
||||||||||||||
чайной величины X : |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
D |
X |
D[ X ] |
|
|
(x |
|
m |
X |
)2 p |
для дискретной случайной ве- |
|||||
|
|
|
|
|
i |
|
|
|
|
|
i |
||||
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
личины; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
D |
X |
D[ X ] |
|
|
(x |
m |
X |
)2 |
|
f (x)dx для непрерывной случайной |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
величины.
Для вычислений дисперсии удобна формула
DX M [ X 2 ] (M [ X ])2 |
2 mX2 . |
Положительное значение квадратного корня из дисперсии случайной величины X называется средним квадратичным отклонением
|
[ X ] |
|
|
X |
D[ X ] DX . |
|
Свойства математического ожидания и дисперсии: |
||||
1. |
M[C] |
C , где C – неслучайная величина; 2. D[C] 0 ; |
|||
3. |
M[X C] M[X ] C ; 4. D[X C] D[X ]; |
||||
5. |
M[CX ] CM[X ]; 6. D[CX ] C 2 D[ X ] ; |
||||
7. |
[CX ] |
|
C |
|
[ X ] ; |
|
|
||||
|
Коэффициент асимметрии определяется по формуле |
||||
|
SX |
3 |
|
|
|
|
3 . |
||||
|
|
|
|
x |
|
|
|
|
|
|
42 |
Если распределение симметрично относительно математического ожи-
дания, то |
SX 0 . Если SX |
0 , то кривая распределения имеет |
||
«скос» с левой стороны; если SX |
0 , то – с правой. |
|||
Эксцесс случайной величины X вычисляется по формуле |
||||
|
4 |
3 . |
|
|
X |
4 |
|
|
|
|
|
|
||
|
X |
|
|
|
Для нормального распределения |
X |
0 . Эксцесс характеризует «ост- |
||
|
|
|
|
|
роверхость» кривой распределения по сравнению с гауссовой кривой.
Для островершинных кривых |
X |
0 , для пологих – |
X |
0 . |
|
|
|
ЗАДАЧИ ДЛЯ АУДИТОРНЫХ ЗАНЯТИЙ
6.1.Построить функцию распределения F(x) индикатора Ia события A, вероятность которого равна p, и начертить ее график.
6.2.Дискретная случайная величина распределения по закону
xi |
–1 |
1 |
2 |
3 |
pi |
0,2 |
0,1 |
0,4 |
0,3 |
Найти функцию распределения F(x) и построить ее график. 6.3. Дан ряд распределения случайной величины X
xi |
–2 |
–1 |
0 |
1 |
2 |
pi |
0,1 |
0,2 |
0,2 |
0,4 |
0,1 |
Требуется: а) построить многоугольник распределения; б) построить функцию распределения F(x) и начертить ее график; в) найти веро-
ятность того, что величина X примет значение, не превосходящее по абсолютной величине 1.
Ответ: в) 0,8
6.4. В урне 5 белых и 25 черных шаров. Вынули один шар. Случайная величина X – число вынутых белых шаров. Построить ряд распределения и функцию распределения F(x) .
0, x 0
Ответ: F(x)= 5/ 6, 0 x 1
1, x 1
43
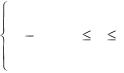
6.5. Бросают три монеты. Случайная величина X – число выпавших "гербов". Требуется: построить ряд распределения и функцию распределения F(x) этой случайной величины.
Ответ: ряд распределения
xi |
0 |
1 |
2 |
3 |
pi |
1/8 |
3/8 |
3/8 |
1/8 |
6.6. Построить ряд распределения и функцию распределения числа попаданий мячом в корзину при двух бросках, если вероятность попадания равна 0,4.
Ответ: ряд распределения
xi |
0 |
1 |
2 |
pi |
0,36 |
0,48 |
0,16 |
6.7. Из партии в 25 изделий, среди которых 6 бракованных, выбраны случайным образом 3 изделия для проверки их качества. Построить ряд распределения случайной величины X – числа бракованных изделий, содержащихся в выборке.
Ответ: ряд распределения
|
xi |
0 |
1 |
2 |
3 |
|
pi |
0,4213 |
0,4461 |
0,1239 |
0,0087 |
6.8. Случайная величина X задана функцией распределения: |
|||||
0, x<2 |
|
|
|
|
|
F(x)= (x 2)2 , |
2 x 3 . |
|
|
|
|
1, x>3 |
|
|
|
|
|
Найти: а) плотность вероятности f (x) ; б) вероятность попадания ве-
личины X в интервал [1;2,5].
Ответ: б) 0,25
6.9. Функция распределения дискретной случайной величины имеет вид
44
|
0, |
x |
|
2 |
|
F (x) |
0,3, |
2 |
x |
3 . |
|
|
0,5, |
3 |
x |
4 |
|
|
1, |
x |
|
4 |
|
Вычислить P{X |
|
3,5} и P{X 2,5}. |
|||
Ответ: 0,5; 0,3
6.10. Случайная величина X распределена по закону, определяемому плотностью вероятности вида
f (x) |
C cos x, |
/ 2 x |
/ 2 . |
|
0, x |
/ 2 |
|
Найти а) константу C; б) функцию распределения F(x) ; в) вычислить вероятность P{| X |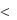
/ 4} .
Ответ: а) 0,5; в) 
2 / 2
6.11. Плотность вероятности непрерывной случайной величины X равна:
0, |
x 1 |
f(x)= x |
1/ 2, 1 x 2 . |
0, |
x>2. |
Построить функцию распределения F(x) и начертить ее график. 6.12. Случайная величина X имеет плотность распределения
0, x 0 |
|
||
f (x)= |
1 |
sin x, 0 x |
. |
|
|||
2 |
|
|
|
0, x> |
|
||
а) Построить функцию распределения F(x) ; б) найти вероятность
того, что величина X попадет на отрезок [0, /4].
Ответ: б) 0,5858/4
45
6.13. Найти среднее квадратичное отклонение случайной величины, заданной рядом распределения
xi |
3 |
5 |
7 |
9 |
pi |
0,4 |
0,3 |
0,2 |
0,1 |
Ответ: 2
6.14. Найти математическое ожидание и дисперсию индикатора Ia события A, вероятность которого равна p.
Ответ: p и pq
6.15. В первой студенческой группе из 24 человек 4 отличника, во второй из 22 человек – 3 отличника, в третьей из 24 – 6 отличников и в
четвертой из 20 – 2 отличника. Случайная величина X – число отличников, приглашенных на конференцию при условии, что из каждой группы случайным образом выбирают по одному студенту. Найти ма-
тематическое ожидание и дисперсию величины X.
Ответ: 0,65; 0,53
6.16.Доказать, что дисперсия числа появлений успеха при однократном проведении опыта не превосходит 1/4.
6.17.Найти математическое ожидание и дисперсию: а) числа очков, выпадающих при бросании одной игральной кости; б) суммы оч-
ков, выпадающих при бросании n игральных костей.
Ответ: а)7/2, 35/12; б) 7n/2, 35n/12
6.18. Сколько изюма в среднем должна содержать калорийные булочки для того, чтобы вероятность иметь в булочке хотя бы одну изюминку была не менее 0,99?
Ответ: 5
6.19. Найти математическое ожидание лотерейных билетов, на которые выпадут выигрыши, если приобретено 40 билетов, а вероятность выигрыша равна 0,05.
Ответ: 2
6.20. Производится 20 независимых испытаний с вероятностью успеха, равной 0,2. Найти дисперсию числа появлений успеха в этих испытаниях.
Ответ: 3,2
46
6.21. Плотность вероятности |
случайной величины X равна |
f (x) Ae | x|.Найти постоянную A, |
математическое ожидание, дис- |
персию, среднее квадратичное отклонение, асимметрию и эксцесс величины X.
Ответ: 0,5; 0; 2; 
2 ; 0; 3
6.22. Плотность вероятности случайной величины X равна
0, x<a
f(x)= 1/ (b a), a x b 0, x>b.
а) Построить функцию распределения F(x) и начертить ее график; б) найти математическое ожидание, дисперсию, асимметрию и эксцесс величины X.
Ответ: б) (a b) / 2 , (b a)2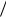 
12 , 0, 1,2
6.23. Смешанная случайная величина X имеет функцию распределения следующего вида. Значения 1 и 2 имеют отличную от нуля веро-
ятность: P{X |
1} |
0,25; P{X 2} |
0,25 . |
При |
x 1 F(x) 0 , |
при x 2 F(x) |
1. На участке 1 x |
2 F(x) |
изменяется по ли- |
||
нейному закону. Найти M[ X ] и D[ X ] . |
|
|
|||
|
|
|
|
|
Ответ: 1,5; 1/6 |
6.24. Случайная величина T имеет плотность вероятности |
|||||
f (t)= 0, t |
0 |
|
|
|
|
e- |
t , t |
0, >0. |
|
|
|
а) Построить функцию распределения |
F(t) |
и начертить ее график; |
|||
б) найти математическое ожидание и дисперсию; в) найти вероятность того, что случайная величина T примет значение, меньшее, чем ее ма-
тематическое ожидание; г) найти P{T M[T ]
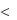
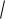
Ответ: б) 1 / , 1/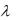 
47
6.25. Время безотказной работы аппаратуры является случайной
величиной T, распределенной по показательному закону. Среднее время безотказной работы 700 часов. Найти вероятность того, что аппаратура проработает больше среднего времени.
Ответ: 0,368
6.26. Производится испытание двух приборов. Время безотказной работы каждого прибора имеет показательное распределение с пара-
метрами |
1 |
для первого прибора и |
2 |
для второго. Приборы выходят |
|
|
|
из строя независимо друг от друга. Найти вероятность того, что за время t0 оба прибора не откажут.
Ответ: e ( 1
2 )t0
6.27. Время безотказной работы радиотехнической системы распределено по показательному закону. Интенсивность отказов системы равна 0,02 (ч–1). Найти среднее время безотказной работы и вероятность безотказной работы за 80 часов.
Ответ: 50 часов; 0,2
6.28. Среднее время работы электронного модуля равно 700 часов. Определить время безотказной работы модуля с надежностью 0,8.
Ответ: 156,2 часов
6.29. Плотность вероятности случайной величины X равна
f (x) |
Ax, 0 |
x |
1 |
0, x |
0, x |
. |
|
|
1 |
Найти постоянную A, математическое ожидание, дисперсию, среднее квадратичное отклонение и асимметрию величины X.
Ответ: 2; 2/3; 1/18; 1 / 3
2 ; 2
2 / 5
6.30. Точка брошена наудачу внутрь круга радиуса R. Вероятность попадания точки в любую область, расположенную внутри круга, пропорциональна площади этой области. Найти функцию распределения и дисперсию расстояния от точки до центра круга.
0, x 0
Ответ: F(x)= x2 /R2 , 0<x<R ; D[ X ] R2 /18 1, x R
48
6.31. Случайная величина X имеет плотность вероятности
|
|
1 |
|
|
( x m )2 |
|
|
|
|
|
|
|
|
|
f(x)= |
|
|
e |
2 2 . |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найти: а) вероятность того, что X примет значение, принадлежащее |
||||||||||||||
интервалу [ |
; |
] ; б) моду и медиану случайно величины X. |
|
|
||||||||||
|
|
|
|
|
|
Ответ: а) |
m |
|
m |
; б) m, m |
||||
|
|
|
|
|
|
|
|
|
||||||
6.32. Случайная величина X имеет нормальное распределение с |
||||||||||||||
параметрами |
|
a |
1, |
|
1. Что больше: P{ 0,5 |
|
X |
0,1} или |
||||||
P{1 X 2}? |
|
|
|
|
|
|
|
|
|
|
|
|||
6.33. Случайная величина X распределена по нормальному закону |
||||||||||||||
N(m, ). Вычислить вероятность Pk |
того, что отклонение величины |
|||||||||||||
X от математического ожидания не превзойдет величины |
k |
при |
||||||||||||
k 1, 2, 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: P |
0,683 ; P |
0,954 ; P |
0,997 |
||||
|
|
|
|
|
|
1 |
2 |
|
|
|
3 |
|
||
6.34. Найти вероятность попадания нормальной случайной величины на участок длиной 2l с центром относительно математического ожидания.
Ответ: 2 (l / )
6.35. Из пункта A ведется стрельба из орудия вдоль некоторой прямой. Предполагается, что дальность полета распределена нормально с математическим ожиданием 1000 м и среднеквадратическим отклонением 5 м. Определить (в %), сколько снарядов упадет с п е- релетом от 5 до 70 м.
Ответ: 30 %
6.36. Доказать, что если случайная величина X имеет нормальное распределение, то линейная функция Y AX B, (A 0) также имеет нормальное распределение.
49