
TeorVer / 8. Функции случайной величины
.pdf
8. ФУНКЦИИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Рассматривается случайная величина Y , зависящая функцио-
нально от случайной величины |
X , т.е. Y (X ) . Пусть случайная |
||||||||
величина X дискретна и известен ее ряд распределения: |
|||||||||
|
x |
x |
… |
xi |
… |
xn |
|
||
|
|
||||||||
Х: |
1 |
2 |
|
|
|
|
|
, |
|
p |
p |
… |
pi |
… |
pn |
||||
|
|
||||||||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
где pi P{X xi }, (i |
1, n |
); pi |
1 . |
|
|||||
|
|
|
|
|
|
i 1 |
|
|
|
После функционального преобразования возможного значения |
|||||||||
случайной величины X , например xi , получаем значение yi (xi )
с вероятностью pi . И так для всех возможных значений случайной величины X . Таким образом, получаем таблицу
(x1 ) |
(x2 ) |
… |
(xi ) |
… |
(xn ) |
|
p |
p |
|
pi |
|
|
, |
… |
… |
pn |
||||
1 |
2 |
|
|
|
|
|
которая в общем случае может не быть рядом распределения случайной величины Y , т.к. значения в верхней строке таблицы могут быть расположены в невозрастающем порядке, а некоторые могут даже совпадать. Для преобразования полученной таблицы в ряд распределения случайной величины Y необходимо упорядочить возможные значения yi (xi ) по возрастанию, а вероятности совпадающих
значений (xi ) нужно сложить.
Если непрерывная случайная величина X с плотностью распределения f (x) связана со случайной величиной Y функциональной
71

зависимостью Y (X ) , то закон распределения случайной величины Y имеет вид
g( y) f ( 1( y)) 1 ( y) ,
где x 1 ( y) – обратная функция.
ЗАДАЧИ ДЛЯ АУДИТОРНЫХ ЗАНЯТИЙ
8.1. Дискретная случайная величина X имеет ряд распределения
|
|
|
|
xi |
|
1 |
|
|
3 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi |
|
0,4 |
|
|
0,1 |
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построить ряд распределения случайной величины Y 2 X . |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
yi |
|
2 |
6 |
|
10 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi |
|
0,4 |
0,1 |
|
0,5 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8.2. Дискретная случайная величина X имеет ряд распределения |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
xi |
|
/ 4 |
|
|
/ 2 |
|
|
|
3 / 4 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
pi |
|
0,2 |
0,7 |
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|||||||
Построить ряд распределения случайной величины Y sin(X ) . |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
yi |
2 / 2 |
|
|
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi |
|
|
|
0,3 |
|
|
0,7 |
||||
8.3. Дискретная случайная величина X имеет ряд распределения |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
xi |
|
–2 |
|
–1 |
|
0 |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
pi |
|
0,1 |
0,2 |
|
0,3 |
|
|
0,3 |
|
|
0,1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

Построить ряды |
распределения случайных |
величин |
|
|
Y X 2 |
1; |
||||||||||||||||||||||||||||
Z |
|
X |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
yi |
|
|
|
1 |
|
2 |
|
5 |
|
|
zi |
|
0 |
|
|
|
|
1 |
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
pi |
|
|
|
0,3 |
|
0,5 |
|
0,2 |
|
|
pi |
|
0,3 |
|
0,5 |
|
0,25 |
|
||||||||||
8.4. Непрерывная случайная величина X имеет плотность |
f (x) . |
|||||||||||||||||||||||||||||||||
Найти плотность вероятности случайной величины Y=2X. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
f ( y) f ( y / 2) |
|
2 |
||||||||||||
8.5. Случайная величина X имеет показательное распределение с |
||||||||||||||||||||||||||||||||||
плотностью вероятности |
f (x) e x , x 0 . Найти функцию распре- |
|||||||||||||||||||||||||||||||||
деления и плотность вероятности случайной величины Y e X . |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
Ответ: |
|
|
|
|
|
|
0, |
y 0 |
|
|
|
0, |
|
y 0 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
F ( y) |
|
|
|
|
f ( y) |
|
|
|
|
|
1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
y, 0 y 1 ; |
1, 0 y |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
y 1 |
|
|
|
0, |
|
y 1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
8.6. Случайная величина распределена по нормальному закону с |
||||||||||||||||||||||||||||||||||
плотностью вероятности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
f (x) |
|
1 |
|
|
|
e x |
2 |
/ 2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найти закон распределения обратной ей величины Y 1/ X . |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: f ( y) |
|
1 |
|
|
|
|
|
e 1/(2 |
2 |
y |
2 |
) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
8.7. Случайная величина X распределена равномерно на отрезке |
||||||||||||||||||||||||||||||||||
[ 1, 2]. Найти плотность вероятности случайной величины Y X 2 . |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, y 0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/(3 |
y ), 0 y 1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: f ( y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
/(6 |
y ), 1 y 4 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, y 4 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
73 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

8.8. Пусть случайная величина X имеет плотность распределения Найти плотность распределения случайной величины:
а) Y aX b , a, b – действительные числа; б) Y 1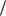 X ;
X ;
в) Y cos(X ) ;
y b |
1 |
, a 0 ; б) |
|
1 |
|
1 |
|
|
|||
Ответ: а) f |
|
|
|
f |
|
|
|
|
, y 0 |
; |
|
|
|
|
|
2 |
|||||||
|
a | a | |
|
|
|
|
|
|
|
|||
|
y y |
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|||
в) [ f (arccosy 2 k) f ( arccos y |
2 k)] |
|
, | y | 1 ; |
|||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
1 y2 |
||||||||||
|
|
|
|
|
|
|
||||
ЗАДАЧИ ДЛЯ ДОМАШНИХ ЗАДАНИЙ |
|
|
|
|
|
|||||
И САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ |
|
|
|
|
|
|
||||
8.9. Случайные величины |
X |
и Y |
независимы, |
|
причем |
|||||
P{X 0} P{X 1} 0,5 , |
P{Y x} x (0 x 1) . |
|
Найти |
|||||||
ф ун к ц ию р асп р едел ени я: а ) |
|
Z1 Y X ; б ) |
Z2 |
Y X / 2 ; |
||||||
в ) Z3 XY . |
|
|
|
|
|
|
|
|
|
|
|
|
|
1, z 0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Ответ: а) F (z) P{Z1 |
|
z / 2, 0 z 1 |
|
|
||||||
z} |
(z 1) / |
|
; |
|||||||
|
|
|
1/ 2 |
2, 1 z 2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, z 2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, z 0 |
|
|
|
|
|
||
|
|
|
|
0 z 1 |
|
|
|
|||
б) F (z) P{Z2 z} |
z / 2, |
|
|
|
||||||
|
(z 1/ 2), |
|
; |
|||||||
|
|
|
1/ 2 |
1 z 3 / 2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, z 3 / 2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, z 0 |
|
|
|
|||
|
|
|
|
|
z / 2, 0 z 1 |
|||||
в) F (z) P{Z3 z} 1/ 2 |
||||||||||
|
|
|
|
1, z 1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
74 |
|
|
|
|
|
|
|
||

8.10. Случайная величина X распределена равномерно в интерва-
ле [ / 2; / 2] . Найти закон |
распределения случайной величины |
||||||
Y sin(X ) . |
|
|
|
|
|
|
|
Ответ: f ( y) |
|
1 |
|
, | y | 1; |
0, y 1, y 1 |
||
|
|
|
|
||||
|
|
|
|
||||
|
1 y2 |
||||||
|
|
|
|
||||
а)
б)
в)
8.11. Плотности независимых случайных величин X и Y равны:
fX |
(x) fY |
(x) |
0, |
x 0 |
|
|
|
||||||
|
|
|
|
x |
; |
|
|||||||
|
|
|
|
|
ae ax , |
0, a 0 |
|
||||||
|
|
(x) fY |
|
0, |
x 0, x a |
|
|||||||
fX |
(x) |
|
|
|
|
|
|
; |
|||||
|
|
|
|
|
1/ a, 0 x a, a |
0 |
|||||||
f |
|
(x) f |
|
(x) |
1 |
|
|
e x |
2 |
/ 2 . |
|
|
|
X |
Y |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Найти плотность распределения случайной величины Z X /Y .
|
|
|
1 |
|
1/ x, 0 x 1 |
||||
Ответ: а) |
fZ (x) |
|
|
, x 0 ; б) |
fZ (x) |
; |
|||
(1 x)2 |
|||||||||
|
|
|
1/ 2x2 , x 1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) fZ (x) |
1 |
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
(1 x2 ) |
||||
8.12. Пусть X и Y независимы и имеют плотности распределения |
|||||||||
f (x) и g( y) |
соответственно. Найти плотности распределения: |
||||||||
а) Z max( X ,Y ) ; б) Z min(X ,Y ) . |
|
|
|
|
|||||
|
|
|
|
z |
|
|
z |
||
|
Ответ: а) |
r(z) f (z) g( y)dy g(z) f (x)dx ; |
|||||||
|
|
|
|
|
|
|
|||
|
|
|
|
z |
|
z |
|||
|
б) r(z) f (z)(1 g( y)dy) g(z)(1 f (x)dx) |
||||||||
|
|
|
|
|
|
||||
|
|
|
|
75 |
|
|
|
|
|
8.13. Доказать, что если случайные величины X и Y независимы и их плотности распределения равны
|
(x) pY |
0, |
x 0 |
|
pX |
(x) |
|
, |
|
|
|
e x , |
x 0 |
|
|
|
|
|
|
то величины X Y и X /Y также независимы.
8.14. Решить предыдущую задачу, если X и Y равномерно распределены на [0; 2] и на [1; 3] соответственно.
Ответ:
0, z 1 |
|
|
|
|
|
1/ 2(z 1/ 2), 1 z 2 |
||
а) r(z) 1/ 2, 2 z 3 |
; |
|
|
|
|
0, z 3 |
|
|
|
|
|
0, z 0 |
|
|
|
0 z 1 |
|
1/ 2, |
||
б) r(z) |
5 / 4, 1 |
z 2 |
z / 2 |
||
0, z 2 |
|
|
|
|
|
8.15. Случайная величина X равномерно распределена на [0; 1]. Показать, что случайная величина Y [X (n 1)] (n — фиксировано,
[.] |
– целая часть) |
имеет "равномерное дискретное" распределение |
|||
pk |
P{Y k} |
|
1 |
|
, k 0, 1, ..., n . |
|
|
|
|||
k |
|
|
|||
|
|
1 |
|||
|
8.16. Показать, |
что случайная величина Y [ln X / ln(1 p)] |
|||
(X и [.] обозначают тоже, что и в предыдущей задаче) имеет геометри- |
|||||
ческое распределение |
p P{Y k} p(1 p)k , k 0, 1, , n . |
||||
|
|
|
|
|
k |
|
8.17. Показать, используя метод математической индукции, что |
||||
|
|
|
|
|
n |
случайная величина |
X n i , где i , i 0, 1, ..., n – независимые |
||||
i 0
76

случайные величины, распределенные равномерно на [0; 1], распреде-
|
|
(x) |
( ln x)n |
|
лена с плотностью вероятности f |
n |
|
, 0 x 1 . |
|
|
||||
|
|
n! |
||
|
|
|
||
8.18. Пусть заданы независимые случайные величины X1 и X 2 , равномерно распределенные на интервале [0; 1]. Образуем новые слу-
чайные величины Y1 и Y2 по формулам |
|
Y1 m 2 ln X 2 cos2 X1, Y2 m |
2 ln X 2 sin 2 X1 . |
Показать, что случайные величины Y1 и Y2 являются независимыми
нормально распределенными с математическим ожиданием m и дисперсией .
8.19. Пусть известна плотность вероятности fX (x) того, что объект расположен на расстоянии X от линзы. Имеет место формула линзы 1/Y 1/ X 1/ F , где F – фокусное расстояние линзы, X и Y – соответственно расстояния от объекта до линзы и от линзы до изображения. Определить плотность вероятности fY ( y) того, что изображение объекта располагается на расстоянии Y от линзы.
|
|
|
|
|
|
Fy |
|
|
F 2 |
|
|
|
Ответ: f |
Y |
( y) |
f |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
|
|
|
X |
|
|
|
( y F ) |
|
||
|
|
|
|
|
y F |
|
|
||||
8.20. Пусть случайные величины X и Y независимы и одинаково |
|||||||||||
распределены, |
причем P{X 1} p 0, P{X 0} 1 p 0 . |
||||||||||
Введем новую случайную величину Z, равную нулю, если |
X Y – |
||||||||||
четное число, |
и единице, если X Y – нечетное число. При каком |
||||||||||
значении p случайные величины X и Z независимы? |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Ответ: 0,5 |
|||
8.21. Пусть X – целочисленная неотрицательная случайная вели- |
|||||||||||
чина, принимающая с вероятностью k |
e |
значения |
k 0, 1, . |
||||||||
|
k! |
|
|
|
|
|
|
|
|
||
Эксперимент состоит в том, что на отрезок [0; 1] независимо одна от
77

другой бросается наудачу X точек. Обозначим |
X i число точек, по- |
|||||||||||||
павших на интервал |
i 1 |
; |
i |
, i 1, 2, ..., n . Доказать, что |
X неза- |
|||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
||
|
|
|
|
|
|
n |
|
n |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
висимы. |
|
|
|
|
|
|
|
|
|
|
|
|
||
8.22. |
Показать, |
|
что |
последовательность |
двоичных |
разрядов |
||||||||
, |
2 |
,..., |
n |
, числа |
X 2 1 ... |
n |
2 n ... |
представляют собой |
||||||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|||
результат n независимых испытаний Бернулли с параметром 1/2, если X – случайная величина, равномерно распределенная на [0; 1].
8.23. Говорят, что случайная величина X 0 имеет логарифмическое распределение с параметрами (m, 2 ) , если Y ln X имеет нормальное распределение N (m, 2 ) . Записать плотность распределения X, найти M[ X ], D[ X ] .
|
|
|
|
1 |
|
|
|
(ln x m)2 |
|
1 |
|
|
|
Ответ: f |
X |
(x) |
|
|
|
exp |
|
|
|
|
|
|
, x 0 ; |
|
|
|
|
2 |
|
|
|||||||
|
|
|
2 |
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
x |
e 2 |
|||||
|
|
M[ X ] e 2 / 2 m , D[ X ] e2m e2 2 |
|||||||||||
8.24. Найти математическое ожидание и дисперсию случайной величины Y, равной сумме случайного числа n независимых одинаково
n
распределенных случайных величин X i : Y Xi , если известны
i 1
M[n], D[n], а M [ X i ] a, D[ X i ] b .
Ответ: aM[n], a2 D[n] bM[n]
8.25. Воспользовавшись результатом предыдущей задачи, найти математическое ожидание и дисперсию случайной величины X, рас-
пределенной по закону n2 с n степенями свободы, если n –
заданное число, – случайная величина, распределенная по биноминальному закону P{ k} Cmk pk (1 p)m k , k 0, 1, , m .
Ответ: n mp; mp(3 p) 2n
