TeorVer / Лекция 12. Характеристичкская функция

Лекция 12

ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ

ЦЕЛЬ ЛЕКЦИИ: построить метод линеаризации функций случайных величин; ввести понятие комплексной случайной величины и получить ее числовые характеристики; определить характеристическую функцию и доказать ее свойства.

Метод линеаризации функций случайных величин

В некоторых частных случаях числовые характеристики функций случайных величин можно найти, используя только числовые характеристики аргументов таких функций. Особенно простые соотношения существуют между числовыми характеристиками функций и числовыми характеристиками аргументов, если функции линейны. Во многих практических применениях нелинейные зависимости в определенном диапазоне заменяются линейными.

Линеаризацией функции называется приближенная замена нелинейной функции линейной, что позволяет достаточно просто находить числовые характеристики функций случайных величин.

Рассмотрим задачу линеаризации функции одного случайного аргумента

Y 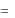( X ) ,

где Y и X – непрерывные случайные величины.

Считая, что некоторая функция (x) дифференцируема, разложим ее в ряд Тейлора в окрестности точки a :

Линеаризация есть приближенное представление функции случайной величины первыми двумя членами ряда Тейлора; при этом разложение про-

водится в окрестности точки математического ожидания mX M[X ] .

106

Это приближение тем точнее, чем меньше диапазон возможных значений случайного аргумента.

Таким образом, при приближенной замене нелинейной функции линейной получаем

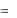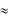Y ( X ) (mX ) 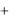(mX )( X 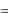mX ) (mX ) 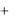(mX ) X .

Необходимо отметить, что при выводе формулы совершен переход от неслучайного аргумента к случайному, что, строго говоря, можно делать с оговорками, так как дифференцировать по случайной величине в общем случае нельзя.

Геометрическая интерпретация метода линеаризации сводится к за-

107

Заметим, что плотность непрерывной случайной величины X , как правило, больше в областях, близких к математическому ожиданию mX .

Поэтому наилучшее приближение нелинейной функции к линейной будет в области математического ожидания случайной величины.

Комплексные случайные величины

Комплексной случайной величиной называется случайная величина

вида

108

Математическим ожиданием комплексной случайной величины

Центрированной комплексной случайной величиной называется случайная величина

где X1, X 2 – действительные центрированные случайные величины.

Дисперсией комплексной случайной величины X X1 jX2 назы-

вается математическое ожидание квадрата модуля соответствующей центрированной случайной величины:

и, воспользовавшись теоремой сложения математических ожиданий (ма-

тематическое ожидание суммы случайных величин равно сумме математических ожиданий), получим

DX M [ X12 X 22 ] DX1 DX 2 .

Дисперсия комплексной случайной величины есть действительное неотрицательное число, равное сумме дисперсий действительной и мнимой частей.

Если есть две комплексные случайные величины X X1 jX2 и Y Y1 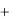jY2 , то определим ковариацию как математическое ожидание произведения центрированной комплексной случайной величины X на центрированную комплексно сопряженную случайную величину Y * :

109

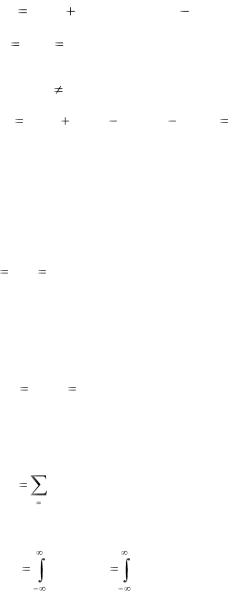
Используя теорему сложения математических ожиданий, получаем

KXY KX1Y1 KX 2Y2 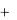j(KX 2Y1 KX1Y2 ) ,

где KX iY j , i 1,2; j 1,2 – ковариации действительных случайных вели-

сопряженной ковариации комплексных величин X и Y .

Характеристическая функция случайной величины и ее свойства

Введем комплексную случайную величину

110

То есть характеристическая функция непрерывной случайной ве-

личины представляет собой преобразование Фурье плотности распределения и однозначно определяется этой плотностью. Отсюда следует, что и плотность распределения f (x) также однозначно выражается через

Основные свойства характеристической функции:

1. Характеристическая функция неслучайной величины a равна

va (t) e jta .

2. Характеристическая функция случайной величины Z aX b ( a и b – неслучайные величины) связана с характеристической функций случайной величины X следующим выражением:

111