Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lektsii_DU_prof_Gromak__chast_2

.pdf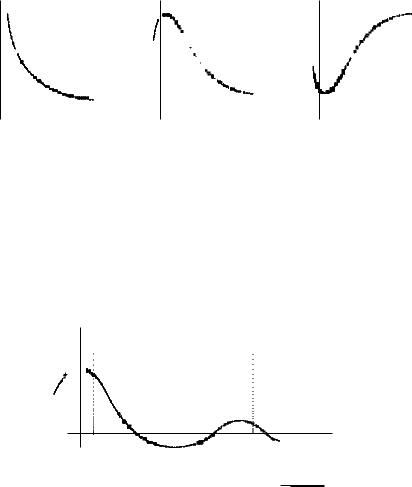

Скачиваний:

Добавлен:

01.03.2016

Размер:

803.88 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Глава 1. Линейные дифференциальные уравнения

касательной к траектории. Сила N уравновешивается сопротивлением стержня, и таким образом, вся система сил эквивалентна f . Очевидно jfj = P sin x = mg sin x . Так как для положительных углов x касательная составляющая f направлена в от-

рицательную сторону, то		f = mg sin x . Очевидно, что S := AM = xl; т.е., x = sl .
Тогда по второму закону Ньютона имеем
m	d2s	= f = mg sin	s	или	d2s	+	g	sin x = 0	(10.5)
	dt2		l		dt2		l

Для малых отклонений имеем sin x x и тогда имеем уравнение гармонического осциллятора (10.2) с !2 = gl .

Пусть сопротивление среды R пропорционально скорости. В этом случае

R= v;

> 0 . Знак ” ” показывает, что сила R направлена противоположно

скорости v . Тогда уравнение движения принимает вид

d2s

(10.6)

+ 2n

+ !2x = 0;

где 2n =

. Характеристическое уравнение (10.6) имеет вид r2 + 2nr + !2 = 0 и с

корнями r1;2 = n p

n2 !2

I. (большое сопротивление). Тогда движение

x(t) = C1er1t + C2er2t

представляет собой апериодическое и не имеет колебательного характера

нет локального

один локальный

экстремума

максимум

минимум

Рис.10.1

II. n2 !2 < 0 (малое сопротивление). Тогда движение

x(t) = Ae nt sin(p

t + )

!2 n2

является квазипериодическим (затухающим) (Рис. 10.2)

Рис.10.2

T -квазипериод, T = p 2

!2 n2

2q! t возрастает с ростом t (см.

Глава 1. Линейные дифференциальные уравнения	22
III. n2 !2 = 0 . Движение определяется

x(t) = (C1 + C2t)e nt

и не является колеблющимся (Рис. 10.1)

Задача 3. (Вынужденные колебания без учета сопротивления среды).

Пусть при условиях задачи 1 на груз действует периодическая сила Q sin pt , где Q и p - постоянные. Тогда пренебрегая массой пружины и сопротивлением среды, находим уравнение движения

d2s	+ !2x = q sin pt;	(10.7)
2	+ !2x = q sin pt;	(10.7)
dt

где q = mQ . Это неоднородное уравнение. Общее решение однородного уравнения имеет вид

xодн = A sin (!t + ):

(10.8)

Найдем частное решение (10.7).

1. p 6= ! (частота вынужденных колебаний не совпадает с частотой собственных колебаний системы). Тогда находя решение в виде x = a cos !t + b sin !t находим

		=	q	sin pt:			(10.9)
	x
			!2 p2
Таким образом, закон движения представляется общим решением
x = A sin (!t + ) +					q	sin pt:	(10.10)

					!2 p2

2. p = ! (частота вынужденных колебаний совпадает с частотой собственных колебаний системы). Явление резонанса.

Будем искать частное решение уравнения

								y• + !2y = qei!t			(10.11)
в виде		y = btei!t . Тогда b =					q	. Следовательно, (10.11) имеет частное решение
в виде		y = btei!t . Тогда b =						. Следовательно, (10.11) имеет частное решение
							2i!
	= Imy = Im		q	tei!t =	qt	cos !t .
x			q		qt
x			2i!		2!
Таким		образом, закон движения системы в резонансном случае имеет вид
Таким
				x = A sin (!t + )					q		(10.12)
										cos !t
									2!	cos !t

Таким образом, амплитуда вынужденных колебаний рис. 10.3).

6
	2q! t
		-
XXXX
	qXXX	XX
	2! t

Рис.10.3

Глава 1. Линейные дифференциальные уравнения

Упражнение 10.1. Исследовать движение системы состоящей из двух связанных пружин с коэффициентами k1 = 4mN ; k2 = 2mN , с грузами m1 = 2кг; m2 = 1кг и одним закрепленным концом (см. рис. 10.4).

	2кг		1кг

AA		AAA

		Рис. 10.4

11 Линейные уравнения Эйлера и Чебышева

1. Рассмотрим некоторые линейные уравнения, приводящиеся к линейным с посто-

янными коэффициентами.
Линейным уравнением Эйлера называется уравнение вида
x(n) + a1	1	x(n 1)	+ a2	1	x(n 2)	+ : : : + anx = 0;	(11.1)
				2
	t			t

где aj 2 C; j = 1; 2; : : : ; n . В (11.1) t = 0 – особая точка. Теорема существования и единственности выполнена для каждого из интервала I1 = (1; 0) и I2=(0; +1) . Положим t = e . Тогда

xt0 = x0 t0 = e x0
		d
xt002 =			(e x0 )e = (x002	x0 )e 2	(11.2)
		dt
: : :	= (x n + : : : + ( 1)n 1(n 1)! x0				)e n
xtn
(n)			(n)

Таким образом, подставляя (11.2) в (11.1), получаем линейное уравнение относи-

тельно

x( ) с постоянными коэффициентами, фундаментальная система которого

состоит из функций вида e

и me . Следовательно, ФСР исходного уравнения

(11.1) состоит из функций вида t и (ln t)mt .

2. Уравнением Чебышева называются уравнения вида

x00

x = 0:

(11.3)

Здесь

точки

t=1; t= 1

особые.

Интервалы однозначной

разрешимости

I1=(1; 1);

I2=( 1; 1); I3=(1; +1) . Положим в (11.3) t = cos . Тогда

	1		1			cos	(11.4)
xt0 = x0			; xt002 = x002		x0
		sin		sin2		sin3

Подставляя (11.4) в (11.3), находим x00 + n2x = 0 . Откуда

x = C1 cos n + C2 sin n или x = C1 cos (n arccos t) + C2 sin (n arccos t) . Частное решение

Tn := cos n arccos t

при n 2 N представляtт собой полином n -ой степени, который называется полиномом Чебышева.

Упражнение 11.1. Доказать, что Tn – полином n -ой степени.

Глава 1. Линейные дифференциальные уравнения

12Общие свойства линейных уравнений второго порядка

Рассмотрим линейное уравнение второго порядка

x00 + p(t)x0 + q(t)x = 0;

где p(t); q(t) : (a; b) ! C и непрерывны.

1. Каноническая форма. Пусть в (12.1) x = (t)y . Тогда имеем

y00 +	z 0		+ p y0 +	00		+ p 0	+ q y = 0:

Положим = e 12 R p(t)dt . Тогда уравнение (??)eq12.2) принимает вид

y00 + I(t)y = 0;

где инвариант I(t) := 12 p0 14 p2 + q .

Пример 12.1. Рассмотрим уравнение Бесселя

	1			+ 1	n2	x = 0; при n =	1
x00	+		x0					; t > 0
		t			t2		2

(12.1)

(12.2)

(12.3)

(12.4)

Положим в (12.4) x = p

. Тогда имеем y00 +y = 0 с ФСР (sin t; cos t) . Следователь-

sin t

cos t

но, ФСР уравнения (12.4) с n = 2

;

. Умножая ФСР на

, получим

так называемые функции Бесселя

I1=2 = r

2 sin t

= r

2 cos t

; I 1=2

2. Самосопряженная

форма.

Умножим

(12.1)

на

(t) .

Тогда

имеем

y00+ py0+ qy=0 . Выбираем так, чтобы

= 0 ,

т.е

= eR p(t)dt .

Тогда

уравнение (12.1) перепишется в форме ( y0)0 + qy = 0 , которую называют самосопряженной.

3.Понижение порядка. Пусть	x1	- частное решение (12.1). Тогда подстановка
R			уравнения, т.е. y		определяется линейным
x = x1 y(t)dt понижает порядок
уравнением первого порядка
y0	+ 2		x10	+ p y = 0:	(12.5)
			x1

Упражнение 12.1. Доказать, что если для уравнения L(x) = 0 известно m частных линейно-независимых решений x1; : : : ; xm; 1 m < n , то порядок уравнения можно понизить на m .

4. Связь с уравнением Риккати. Положим в уравнении (12.1) xx0 = y(t) , где y = y(t) - новая искомая функция. Тогда z(t) определяется уравнением Риккати

y0 + y2 + py + q = 0:

(12.6)

Глава 1.

Линейные дифференциальные уравнения

Справедливо

обратное

утверждение:

любое

уравнение

Риккати

y0=P (t)y2+Q(t)y+R(t) можно свести к линейному

уравнению

второго

порядка

заменой y =

xx0 .

(t)

5. Связь между решениями. Пусть x1 и

x - решения уравнения (12.1). То-

гда по формуле Лиувилля-Остроградского W (t) =

= Ce R p(t)dt или

x10

x =

0 x2

= Ce p(t)dt

или

x12 e R p(t)dtdt + C1x1:

(12.7)

x = Cx1

Таким образом, если x1 - решение, то x2 = x1

e R

p(t)dt

dt также решение.

x12

13Интегрирование линейных уравнений при помощи степенных рядов

Пусть дано уравнение
x00 + p(t)x0 + q(t) = 0;		(13.1)
в котором коэффициенты p(t); q(t)	голоморфны в точке t0 2 (a; b)	так что
1	1

p(t) =	pj(t t0)j; q(t) =	qj(t t0)j	(13.2)
	j=0	j=0

Тогда, согласно теореме Коши, уравнение (13.1) имеет единственное решение, голоморфное в точке t = t0 и принимающее в этой точке вместе со своей производной любые наперед заданные значения x0 и x00 , т.е решение вида

1
Xk
x = x0 + x00 (t t0) + Ck(t t0)k;	(13.3)
=2

причем ряд (13.3) сходится в области jt t0j < > 0 . При этом радиус сходимости не меньше расстояния от t0 до ближайшей из точек, в которых p(t) или q(t) теряют аналитичность (т.е. особых точек). Выбирая начальные условия решений x1(t); x2(t) так, чтобы

	x1(t0) x2(t0)

W (t0) =	x10 (t0) x20 (t0) 6= 0;		x	t	; x	t	) с разложени-
получаем два голоморфных линейно	независимых решения			1( )		2(	) с разложени-
ями (13.3), которые составляют ФСР в области jt t0j < .
Пример 13.1. Будем искать решения x1(t); x2(t) уравнения
x00 tx = 0							(13.4)
в виде		1
1		1
X		Xk
x1 = 1 + Ck(1)tk; x2 = t +		Ck(2)tk					(13.5)
k=2		=2

Глава 1. Линейные дифференциальные уравнения

так что W [x1(t0); x2(t0)] = 1 6= 0 . Подставляя x1

в (13.4), находим

t0 :

1 C2(1) = 0

t :

2 C3(1) 1 = 0

t2 :

3 C4(1) = 0

t3 :

4 C5(1) C2(1) = 0

: : :

tk 2 : k(k 1)Ck(1) Ck(1)3 = 0

Откуда C(1)=0; C

(1)

; C(1)=0; C(1)

=0; C(1)

C3(1)

; : : : ; C(1)

6 5

3!5 6

2 3 5 6:::(3k 1)3k

Следовательно,

t3k

Ai(t) := x1 = 1 +

+ : : : +

+ : : :

2 3

2 3 5 6

2 3 5 6 : : : (3k 1)3k

Аналогично находим

t3k+1

Bi(t) := x2 = t +

+ : : : +

+ : : :

3 4

3 4 6 7

3 4 6 7 : : : 3k(3k + 1)

Функции Ai(t); Bi(t) называют функциями Эйри, которые являются целыми функциями t . Общее решение уравнения (13.4) имеет вид x = C1Ai(t) + C2Bi(t) .

14Интегрирование при помощи обобщенных степенных рядов

Выше мы показали, что уравнение Бесселя с индексом n = 1=2

	1				1=4		(14.6)
x00	+		x0 +	1		x = 0
		t			t2

имеет ФСР вида

2 sin t

J1=2 :=

t1=2

+ : : :

(14.7)

2 cos t

J 1=2 :=

t 1=2

: : :

(14.8)

В уравнении (14.6) точка t = 0 является особой, а решения в окрестности t = 0 (14.6) и (14.7) представлены в виде так называемых обобщенных степенных рядов.

Определение 14.1. Обобщенным степенным рядом по степеням t t0 называется ряд вида

		1
	(t t0)	Xk	(14.9)
	(t t0)	ak(t t0)k;	(14.9)
		=0
где 2 C , а	k1=0 ak(t t0)k; a0 6= 0 - сходящийся степенной ряд. При этом под
комплексной	степенью понимается следующее
комплексной	P

(t t0) + = e( + ) ln (t t0) = e ln (t t0)e ln (t t0) =

= (t t0) (cos( x ln (t t0)) + sin( x ln (t t0))):

Глава 1. Линейные дифференциальные уравнения	27
Рассмотрим линейное уравнение
x00 + p(t)x0 + q(t) = 0:	(14.10)

Определение 14.2. Особая точка t = t0 коэффициентов p(t) и q(t) называется регулярной, если функции (t t0)p(t) и (t t0)2q(t) голоморфные в окрестности t = t0 , то есть уравнение (14.10) в окрестности регулярной особой точки может быть представлено в виде

x00 + t	1 t0	=0 pj(t t0)j!x0	+	(t	1t0)2	j=0 qj(t t0)j!x = 0;	(14.11)
		1				1
		Xj				X

где степенные ряды, входящие в коэффициенты, являются сходящимися в области jt t0j < r; r > 0 .

Заметим, что точка t = 0 для уравнения Бесселя есть регулярная, а точка t = 1 является особой, но не регулярной, т.е. иррегулярной.

В окрестности особой точки решение в виде степенного ряда может не существовать. Однако, справедлива следующая

Теорема 14.1. (Фукс) Пусть t = t0 - регулярная особая точка уравнения (14.10), причем степенные ряды, входящие в коэффициенты (14.11), сходятся в области jt t0j < R , тогда в окрестности t = t0 существует, по крайней мере, одно решение в виде обобщенного степенного ряда (14.9), причем степенной ряд, входящий в (14.9), заведомо сходится в области jt t0j < r; r > 0 .

Пусть t0 = 0 . Тогда, подставляя ряд

1
Xk	6= 0	(14.12)
x = Cktk+ ; C0	6= 0	(14.12)
=0

в уравнение

1	!	1 !
X		X
t2x00 + t	pktk x0 +	qktk x = 0;
k=0		k=0

получаем систему для определения и Ck :

t0 : ( ( 1) + p0 + q0) C0 = 0

k 1

1) +

: ((

)( +

( +

) +

0) k + Pn=0

(

k n(

+ ) +

k n)

n =(14.13)

где k = 1; 2; : : : . Так как C0

6= 0 , то для определения имеем так называемое

определяющее уравнение

f0( ) := ( 1) + p0 + q0 = 0:

(14.14)

Заметим, что здесь p0 = limt

0 tp(t) , q0

= limt

0 t2q(t) . Коэффициент при Ck

имеет

вид

f0( + k) := ( + k)( + k 1) + p0

( + k) + q0:

(14.15)

Пусть 1 и 2 корни определяющего уравнения. Если разность 1 2 не есть целое число, то f0( 1+k) 6= 0; f0( 2+k) 6= 0 ни при каком целом k > 0 , а значит, указанным методом можно построить два линейно независимых решения

1	1
X	Xk
x1 = t 1	Ck(1)tk; x2 = t 2	Ck(2)tk	(14.16)
k=0	=0

Глава 1. Линейные дифференциальные уравнения

Если же разность 1 2 2 Z , то указанным методом можно построить одно решение в виде обобщенного степенного ряда. Зная это решение, с помощью формулы Лиувилля - Остроградского можно найти второе решение

x2(t) = x1(t) x1 2(t)e p(t)dtdt:

15 Уравнение Бесселя

В качестве примера приложения обобщенных степенных рядов рассмотрим уравнение Бесселя.

x00 +	1	x0	+	t2 2	x = 0	(15.1)

	t			t2

имеющее широкие приложения в задачах физики и техники.

В уравнении (15.1) t = 0 является регулярной особой точкой. Решение в окрестности точки t = 0 будем искать в виде

	n
	Xk	6= 0	(15.2)
x = t	cktk; c0	6= 0	(15.2)
	=0
Тогда для определения q имеем определяющее уравнение
( 1) + 2 = 0;			(15.3)

имеющее при 6= 0 два различных корня 1 = ; 2 = . Коэффициенты Ck для q1 = в (15.2) определяются из системы

(: : :+ 1)2 2)C1 = 0

(15.4)

2 2

( + k) )Ck + Ck 2 = 0

Откуда при = имеем C2k+1 = 0 , C2k = ( 1)k

: Та-

22kk!( + 1)( + 2) : : : ( + k)

ким образом, в соответствии с теоремой Фукса, имeем решение

C0 t2k

22kk!( + 1)( + 2) : : : ( + k) =

x1(t) := t

( 1)k

C0 2

+2k

k=0( 1)k k!( + 1)( + 2) : : : ( + k)

Выберем C0 так, чтобы коэффициенты ряда имели наиболее компактный вид. С

этой целью рассмотрим гамма-функцию, определяемую интегралом

(z) := Z0

e ttz 1dt; Re[z] > 0;

(15.5)

зависящим от параметра z . Эта функция обобщает факториал, так как справедливы свойства: (z + 1) = z (z); (1) = 1 . Следовательно, (k + 1) = k!; k 2 N если

Глава 1. Линейные дифференциальные уравнения

k 2 N [ f0g . Для Re[z]

0 гамма-функцию можно определить аналитическим

продолжением (15.5) либо через предел

(z) = lim

1 2 3 : : : n

n!1 z(z + 1) : : : (z + n)

Заметим, что в точках z

= 0; z = 1; : : : ; z = n; : : :

гамма-функция обращается в

бесконечность.

Упражнение 15.1. Доказать, что

(z) (1 z) =

. Эта формула носит

sin( z)

название формулы дополнения.

Выберем C0

. Тогда решение принимает вид

2 ( + 1)

+2k

(15.6)

J (t) := x1(t) = k=0( 1)k k! ( + k + 1)

Функция J (t)

называется функцией Бесселя первого рода

го порядка.

Будем искать второе решение, соответствующее второму показателю = . Тогда из системы (15.3)

( 2 + 1)C1 = 0

C2k 1

C2k+1 = (2k 1)( 2 + 2k + 1)

C2k 2

C2k = 22k( + k)

Таким образом, возможны следующие случаи.

I:6= m + 1=2; 6= m; m 2 N[f0g

В этом случае все коэффициенты C2k+1; C2k определяются единственным образом с точностью до выбора C0 . Пусть

C0 =

2 ( + 1)

Тогда

+2k

(t) := x2(t) = k=0( 1)k k! ( + k + 1)

(15.7)

Упражнение 15.2. Доказать, что решения x1; x2

линейно независимые.

Пусть =

2m+1

для некоторого целого

m . Тогда в системе (15.4) имеем урав-

нение 0 C2m+1 = 0 . Полагая C2m+1 = 0 , получаем второе решение такое же, как и (15.6).

Пример 15.1. Решить уравнение
t2x00 + tx0 + (t2		1	)x = 0:

		4
Решение. Это уравнение Бесселя с = 1=2		. Поэтому
1		1		t	1=2+2k
x1 = J1=2(t) = X( 1)k
x1 = J1=2(t) = X( 1)k	k! (3=2 + k)			2

k=0

Глава 1. Линейные дифференциальные уравнения

Так как (1=2) = p

,то (3=2) = (1 + 1=2) = 1 (1=2) = 1 p

(1=2 + 2) = 232 p ; : : : ; (21 + k) =

1 3 5 72k

:::(2k

Следовательно,

21 +2k

x1 = J1=2(t) = k=0( 1)k

1)p

k!1

7 : : : (2k

t2k+1

( 1)k

= r t k=0

(2k + 1)! = r t sin t:

Аналогично,

x2 = J 1=2(t) = r

cos t

Общее решение исходного уравнения имеет вид

x = r

(C1 sin t + C2 cos t)

Замечание 15.1. Функции Бесселя c =

2m+1 выражаются через элементарные

функции вида

= r

J2 2

(Pm( t ) sin t + Qm( t ) cos t);

m+1

где Pm и Qm полиномы степени m .

Пусть = m; m 2 N . Тогда имеем C2n = C00 = 1 , так как C0 6= 0 . В этом случае второе решение нельзя найти в виде обобщенного степенного ряда. Оно должно содержать логарифм.

Упражнение 15.3. Доказать, что для целого > 0 J = ( 1) J .

В случае целого введем функцию Бесселя порядка второго рода.

Y	(t) = lim Y	"	(t) = lim			( 1)kJ (n ")(t) Jn "
	" 0	"	"	!	0	"
	!			!		"

Такой предел существует и Y (t) есть решение уравнения Бесселя. В этом случае общее решение уравнения Бесселя имеет вид

x = C1J (t) + C2Y (t)

16 Колебательный характер решений уравнений

второго порядка. (Введение в теорию Штурма.)

Рассматриваем уравнения

x00 + p(t)x0 + q(t)x = 0;

(16.1)

где p(t); q(t) : (a; b) ! R и непрерывны. Нулями решения x(t) называем вещественные корни уравнения x(t) = 0 .

Теорема 16.1. Все нули ненулевого решения x = x(t) уравнения (16.1), лежащие внутри интервала (a; b) , изолированы.

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.11.2019552.96 Кб4lektsia_7_rabota_s_bolshimi_dokumentami.doc
#
13.09.201933.71 Кб2lektsia_8.docx
#
16.07.201949.45 Кб4Lektsii.docx
#
25.11.2018249.34 Кб3Lektsii_1-3.doc
#
13.09.2019250.37 Кб13lektsii_bukhgalteria.doc
#
01.03.2016803.88 Кб12Lektsii_DU_prof_Gromak__chast_2.pdf
#
03.09.2019105.98 Кб15Lektsii_IGiPZS.docx
#
23.11.2019483.84 Кб79Lektsii_IGPB.doc
#
29.02.2016383.97 Кб159Lektsii_Laguna.docx
#
01.03.201623.1 Mб12Lektsii_Levakova_po_matanalizu.pdf
#
29.02.20161.41 Mб6Lektsii_Mekhanika_Ch_1.pdf