
Lektsii_Mekhanika_Ch_1
.pdf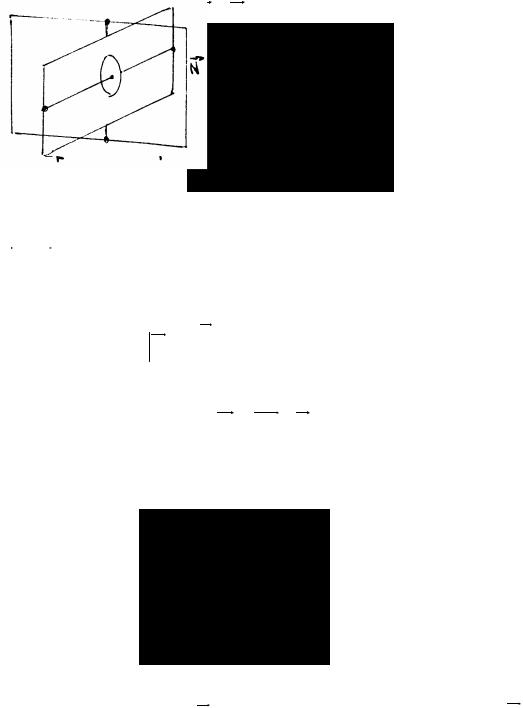
14.7. Гироскопы.
Рассмотрим быстро вращающийся относительно оси симметрии массивный диск (рис.64). При очень быстром вращении диска, как было сказано выше, векторы момента импульса и угловой скорости направлены вдоль оси симметрии.
Если к концам оси вращения приложить пару сил, ее момент будет изменять момент импульса в соответствии с уравнением моментов:
d N = Mdt
рис. 64)
Через промежуток времени dt момент импульса изменит свое направление и станет
равным N + d N Соответственно изменится и положение оси симметрии. Как видно, силы пары приложены в горизонтальной плоскости, а ось вращается под действием момента - в вертикальной.
Уравнение моментов в скалярном виде в этом случае представляют следующим образом:
M |
|
= |
d N |
= |
Nωпр |
dt |
= Nω |
пр |
|
||||||||
|
|
|
|
|||||
|
dt |
dt |
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
С учетом направлений векторов уравнение моментов для быстро вращающегося тела записывает в векторной форме так:
M = ωпр × N |
(273) |
Гироскопом называют массивное тело, очень быстро вращающееся вокруг оси симметрии. Наиболее часто применяются гироскопы в кардановых подвесах. В таких подвесах при любом повороте оси вращения центр масс гироскопа остается неподвижным (рис.65) Нa рисунке представлен карданов подвес для гироскопа с двумя степенями свободы.
Рис.65 Для определения угловой скорости прецессии удобно пользоваться следующими
соображениями. Масштаб измерения N можно выбрать таким, что конец вектора N совпадает с концом оси гироскопа (рис. 66).
При действии на конец оси (в т. А) силы F По уравнению моментов
(рис. 66)
ее момент вызовет прецессионное вращение.
M = |
d N |
= |
d(CA) |
|
|
dt |
dt |
|
|
||
|
|
|
|||
Но CA можно рассматривать как радиус-вектор т. A относительно центра масс. Тогда, |
|||||
по определению: |
|
|
|
|
|
|
|
M = vA |
(274) |
||
14.8. Прецессия волчка.
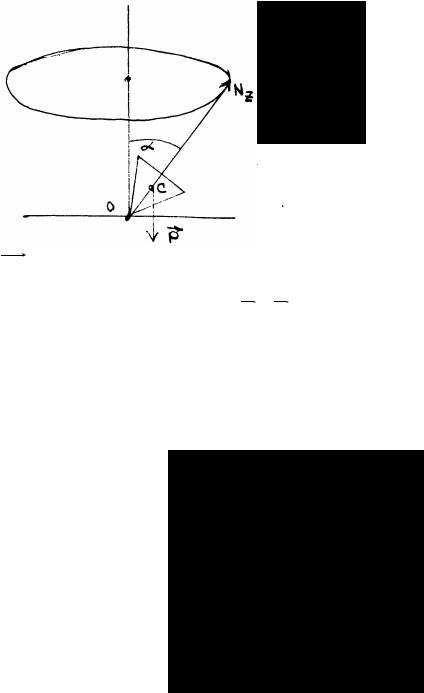
Быстро вращающийся симметричный волчок установлен на горизонтальную поверхность (рис. 67). Точка касания O неподвижна. Прецессия волчка вызывается моментом силы тяжести, так как линия действия реакции проходит через неподвижный центр O .
При указанном направлении вращения момент силы тяжести вызывает прецессию в направлении, указанном на рисунке. Угловую скорость прецессии
(рис. 67)
можно определить, пользуясь (274):
mg OC sinα = Izωzωпр sinα
т.е.
ω = |
mg OC |
(275) |
пр |
Izωz |
|
Следовательно, угловая скорость прецессии тем меньше, чем больше угловая скорость собственного вращения.

15. ГИДРОСТАТИКА.
Гидромеханика изучает свойства покоя и движения жидкостей и газов. Гидростатика изучает только свойства покоя жидкостей и газов.
Основные соотношения гидромеханики получены для идеальной жидкости, т.е. для абсолютно несжимаемой и невязкой жидкости.
Основной задачей гидростатики является нахождение распределений давления и плотности по объему жидкости или газа (в случае идеальной жидкости - только давления).
15.1.1.Давление покоящейся жидкости.
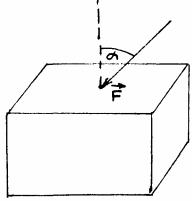 (рис.68)
(рис.68)
Выделим в объеме покоящейся жидкости небольшой объем (рис. 68), пусть на грань этого объема действует со стороны окружающих слоев сила давления F.
Из опыта известно, что трение покоя в жидкостях отсутствует, т.е. должны отсутствовать касательные усилия к выделенной грани.
Средним давлением называют величину:
p |
ср |
= F |
|
S |
|
|
|
где dF сила давления, действующая на площадку площади dS. Истинным давлением или давлением в точке называют величину:
p = lim p |
|
= |
dF |
(276) |
ср |
|
|||
t→0 |
|
dS |
|
|
|
|
|
В покоящейся жидкости давление в точке не зависит от ориентировки площадки, на которую оно действует, действительно, в покоящейся: жидкости выделим небольшой объем, форма которого показана на рис. 69. На каждую грань объема действует силы давления, поскольку объем покоится, в каждом из координатных направлений сумма сил равна нулю:
OX : px S OBC − pn S ABC cos(x n)= 0
т. к.
S ABC cos(x n)= S OBC ;(px − pn ) S OBC = 0
т.е.
px = pn

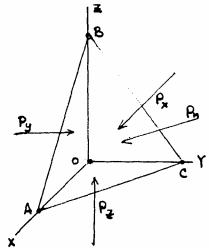 (рис. 69) Аналогично можно показать, что:
(рис. 69) Аналогично можно показать, что:
py = pn
Следовательно:
px = py = pz = pn
15.2.Уравнение гидростатики Эйлера
Впокоящейся жидкости выделим малый ее объем dV=dxdydz в форме прямоугольного параллелепипеда (рис. 70).
Известно давление в центре объема p и изменение давления на единицу длины в
каждом из координатных направлений:
δp δp δp δx ; δy ; δz
На каждую грань объема действуют силы давления, а на весь объем - объемные (массовые) силы, например, сила тяжести. Поскольку объем покоится, сумма проекции всех сил по каждому из координатных направлений равна нулю.
На заднюю грань действует сила давления:
|
|
1 δp |
||
dFx |
= p − |
|
|
|
2 δx |
||||
|
|
|||
dx dydz
а на переднюю:
′ |
|
1 δp |
||
dFx |
= p + |
|
|
|
2 δx |
||||
|
|
|||
dx dydz
Кроме того, в этом направлении действует составляющая массовой силы dθ, которую можно определить по второму закону Ньютона:
dθx = ρdVax
где: ρ - плотность среды, ax- ускорение, которое способна сообщить массовая сила. Т. к. объем покоится,

dFx − dFx′ + dθx = 0
т.е.
|
1 δp |
|
|
1 δp |
|
|||
p − |
|
|
dx dydz − p + |
|
|
dx dydz + |
||
2 δx |
2 δx |
|||||||
|
|
|
|
|||||
Поскольку dV ≠ 0 :
1 δp
ax = ρ δx = 0
|
− |
δp |
|
ρaxdydxdz = |
δx |
+ ρax dxdydz |
|
|
|
|
|
|
|
|
(277) |
Аналогично для других координатных направлений:
a |
|
− |
1 |
|
δp = 0 |
(278) |
|
y |
|
|
|||||
|
|
|
ρ δy |
|
|||
a |
|
− |
|
1 |
δp = 0 |
(279) |
|
z |
|
|
|||||
|
|
|
ρ δz |
|
|||
(277), (278), (279) и представляют собой систему уравнений гидростатики Эйлера.
15.3. Уравнение поверхности уровня
Поверхностью уровня называют такую поверхность, во всех точках которой
давление одинаково (dP=0) |
|
|
|
dp = |
δp dx + |
δp dy + |
δp dz |
|
δx |
δy |
δz |
то, с учетом уравнение Эйлера: |
|
|
|
dp = ρ[axdx + aydy + azdz] |
|
|
|
для поверхности уровня: |
|
|
|
ρ(axdx + aydy + azdz)= 0 |
(280) |
||
В случае идеальной жидкости: |
|
|
|
axdx + aydy + azdz = 0 |
(281) |
||
Пример, Пусть жидкость покоится в поле тяготения 3емли.
Плоскость 0XY горизонтальна, а ось z направлена вертикально вверх. В этом
случае:
ax = ay = 0,az = −g
Тогда:
− gdz = 0
т.е. z=const, т.о. поверхности уровня (в частности, свободная поверхность) горизонтальны.
15.4. Закон Паскаля
Жидкость покоится в поле тяготения Земли. В этом случае уравнения Эйлера имеют вид:
− |
|
1 |
δp = 0 |
(282) |
|||
|
|
|
|||||
|
|
ρ δx |
|
||||
− |
1 |
δp = 0 |
(283) |
||||
|
|||||||
|
ρ δy |
|
|||||
− g − |
1 |
δp = 0 |
( 284) |
||||
|
|||||||
|
|
|
|
|
ρ δz |
|
|
С учетом (282) и (283) последнее уравнение (284) принимает вид:
− g − |
1 |
δp = 0 |
(285) |
|
|||
|
ρ δz |
|
|
откуда:
dp = −ρgdz = −γdz |
(286) |
где γ = ρg удельный вес жидкости. Интегрируя (286), получаем |
|
p = −γz + C |
(287) |
Постоянная интегрирования будет определена, если в точке с координатой z0 известно давление p0 . Тогда
C = p0 +γz0
p = p0 + γ (z0 − z)
Последнее выражение обычно записывают в виде:
z + |
p |
= z |
|
+ |
p0 |
= const |
(288) |
|
0 |
|
|||||
|
γ |
|
γ |
|
|
||
|
|
|
|
|
|||
т.е. для жидкости, покоящейся в поле тяготения Земли, сумма геометрической (Z) и пьезометрической (p/γ)) высот для всех точек объема жидкости одинакова. Это и есть закон Паскаля.
15.5.Сообщающиеся сосуды
15.5.1.Сообщающиеся сосуды заполнены однородной жидкостью
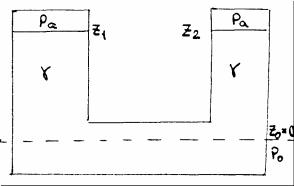
Свободные поверхности в левом и правом коленах находятся на уровнях Z1 и Z2, а давление на этих поверхностях равно атмосферному Рa. Сравним свободные поверхности с общей для обоих сосудов частью, уровнем Z0, на котором давление равно P0, как показано на рис. 71.
z |
+ |
|
pa |
= |
|
p0 |
||
|
|
|
|
|||||
|
1 |
|
|
γ |
|
|
|
γ |
|
|
|
|
|
|
|
||
z |
|
+ |
pa |
|
= |
p0 |
||
2 |
γ |
|
γ |
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
Откуда:
z1 = z2
(рис. 71)
Следовательно, свободные поверхности устанавливаются на одном уровне.

15.5.2. Сообщающиеся сосуды заполненные неоднородной жидкостью
(рис. 72)
Положим, что сосуды заполнены неоднородной жидкостью (несмешивающимися жидкостями с удельными весами γ1 и γ2. Через границу раздела жидкостей проводим уровень Z0 =0, на котором давление равно Р0 (рис. 72).
Сравним свободную поверхность в левом сосуде с границей раздела со стороны жидкости с удельным весом γ1:
z + |
|
p1 |
|
= |
p0 |
|
(289) |
|||||||
|
|
γ |
|
|
|
|||||||||
1 |
|
γ |
1 |
|
|
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
для правого сосуда аналогично: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
+ |
p2 |
= |
|
p0 |
(290) |
|||||||
2 |
|
|
γ |
|
|
|||||||||
|
|
|
γ |
2 |
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Сравнивая записанные выражения, получим, что свободные поверхности в сосудах устанавливаются на уровнях, обратно пропорциональных удельным весам жидкостей:
z1 |
= |
γ 2 |
(291) |
|
z2 |
γ1 |
|||
|
|
15.5.3. Закон Архимеда
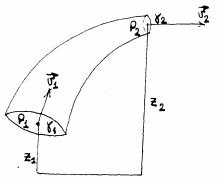
Тело погружено в жидкость (рис. 73).
Рис.73.
На его поверхность со стороны жидкости действуют силы давления, выделим в теле объем малого сечения, ось которого вертикальна. На верхнюю и нижнюю грани этого объема действуют силы давления:
dF = p1dS1,dF′ = p2dS2
Равнодействующая сил давления в проекции на вертикальную ось равна: dFz = (p1 − p2 )dS
где: dS - проекция dS1 (или dS2) на горизонтальную плоскость. Разность давлений по закону Паскаля равна
p = p1 − p2 = (p2 +γ z)− p2 = γ z
где: dZ - разность уровней центров граней выделенного объема. Тогда равнодействующая сил давления равна
dFx = γ zdS = γdV
где dV - величина выделенного объема.
Вертикальная проекция сил давления, действующих на всю смоченную поверхность тела, может быть получена путем интегрирования предыдущего выражения:
Fx = ∫dFz = γV =θ
(V )
т.е. сила, действующая со стороны жидкости на погруженное в нее тело по величине равна весу жидкости, вытесненной телом.
Формулировка закона: на тело, погруженное в жидкость действует выталкивающая сила, равная весу жидкости в объеме, вытесненном телом, и приложенная в той точке смоченной поверхности тела, в которой вертикаль, проведенная через центр масс вытесненной жидкости, пересекает эту поверхность.
Существенным в формулировке закона Архимеда является правильное указание точки приложения выталкивающей силы. Действительно, поскольку сила Архимеда обусловлена действием распределенных по поверхности сил давления со стороны жидкости, то и равнодействующая сил давления должна быть приложена к смоченной поверхности тела (но не к центру масс вытесненной жидкости, как это часто утверждается). Кроме того, наличие в плавающем теле деформаций можно объяснить только при таком рассмотрении силы Архимеда.
15.6. Механика движущихся жидкостей.
ВВЕДЕНИЕ
При изучении движения жидкостей и газов применяются различные способы описания движения. Наиболее часто используется метод, предложенный Эйлером. Но Эйлеру в области пространства, занятой движущейся жидкостью, выделяется точка, в которой определяются параметры движения различных жидких частиц, проходящих через эту точку в различные моменты времени.
Основной задачей механики движущейся жидкости является нахождение распределений скорости, плотности и давления по потоку жидкости:
vx = vx (x, y, z,t)
vy = vy (x, y, z,t)
vz = vz (x, y, z,t)
ρ= ρ(x, y, z,t)
p = p(x, y, z,t)
Для установившегося потока, когда параметры потока в фиксированной точке его не изменяются с течением времени, задача сводится к нахождению распределений:
vx = vx (x, y, z),
vy = vy (x, y, z),
vz = vz (x, y, z),
ρ= ρ(x, y, z),
p = p(x, y, z,t).
Ещё более упрощается задача для идеальной жидкости. В случае установившегося потока идеальной жидкости необходимо найти распределения:
vx = vx (x, y, z),
vy = vy (x, y, z),
vz = vz (x, y, z),
p = p(x, y, z,t).
ОПРЕДЕЛЕНИЯ
1.Линией тока называют кривую, в каждой точке которой касательные к ней совпадают по направлению с вектором скорости в данный момент времени.
2.Поверхностью тока называют поверхность, образованную линиями в тока. 3.Поверхность тока, проходящую через замкнутый контур, называют трубкой тока. 4.Часть потока жидкости, ограниченную трубкой тока, называют струёй жидкости. Пpи установившемся потоке жидкость внутри трубки тока а движется как в трубке
с твердыми стенками.
15.7. Расход жидкости
Различают объемный, массовый и весовой расходы жидкости. Объемным расходом называют объем жидкости, протекающий в единицу времени через заданную площадку. Для площадки элементарно малой площади dS объемный расход равен:
dV = vdS
Аналогично массовый расход определяется величиной протекающей через площадку массы жидкости в единицу времени:
dM = ρdV = ρvdS
Вес жидкости, протекающей через площадку в единицу времени, называют весовым расходов:
dθ = γdV = γvdS
В этих выражениях: v - скорость жидкости, ρ - плотность жидкости, γ - удельный вес жидкости.
15.8. Уравнение неразрывности струи жидкости
Оделим участок струи жидкости (рис.74). Через левое сечение площади S1 в участок трубки тока в единицу времени втекает жидкость со скоростью v1, принимаемой одинаковой по сечению. Массовый расход жидкости в этом сечении равен:
M1 = ρ1v1S1
Аналогично массовый расход для правого сечения равен:
M2 = ρ2v2S2

(рис. 74)
Для того, чтобы в выделенном участке трубки тока не происходило накопление жидкости или, наоборот, уменьшение массы, массовые расходы в левом и правом сечениях должны быть равны. Такой вывод можно сделать для любого другого сечения, т.е.:
ρvS = const
Это и есть уравнение неразрывности струн жидкости. В случае несжимаемой жидкости:
vS = const
15.9. Уравнение Бернулли
Как и для твёрдых тел, для жидкости полная механическая энергия состоит из потенциальной и кинетической энергии, кинетическая энергия движущейся массы жидкости равна:
Ek = Mv2
2
Что касается потенциальной энергии, то она будет определяться не только положением жидкости в поле тяготения Земли, но и внутренним состоянием ее. Соответственно, различают потенциальную энергию положения:
Ep1 = Mgz
Ипотенциальную энергию состояния жидкости:
Ep2 = pV
Полная энергия движущейся жидкости равна:
E |
|
= E |
|
+ E |
|
+ E |
|
= |
Mv2 |
+ Mgz + pV |
(292) |
0 |
k |
p1 |
p2 |
|
|||||||
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
Удельной энергией называют полную энергию, приходящуюся на единицу веса жидкости:
l |
|
= |
E0 |
= z + |
p |
+ |
v2 |
(293) |
0 |
|
|
|
|||||
|
|
θ |
|
γ 2g |
|
|||
|
|
|
|
|
||||
В такой записи все члены удельной энергии имеют размерность длины и называются соответственно: геометрической, пьезометрической высотой и высотой скоростного напора
.  (рис. 75)
(рис. 75)
