
Lektsii_Mekhanika_Ch_1
.pdf
|
|
r2 + R2 |
− r2 |
|
|
|
|
|
|
|
|
|
|
γmM r − |
|
1 |
r dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2r |
|
|
1 1 |
|
γmM(r |
2 |
− R |
2 |
2 |
)dr1 |
dF = − |
|
|
|
|
= − |
|
|
+ r1 |
||||
|
2r3rR |
|
|
|
|
4r2 r2 R |
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
Сила взаимодействия со всем слоем, если точка находится за его пределами равна:
r+R |
γmM r+R |
r2 |
− R2 |
r+R |
|
|
γmM |
|||
F = ∫ dF = − |
|
2 |
∫ |
|
|
dr1 + ∫dr1 |
|
= − |
|
|
|
|
2 |
|
2 |
||||||
r−R |
4r |
|
R r−R |
|
r1 |
r−R |
|
|
r |
|
Если же точка находится внутри слоя, сила взаимодействия равна:
R+r
F = ∫dF = 0
R−r
(229)
(230)
(231)
12.5.3. Взаимодействие между точечной массой и однородным шаром.
Точка массы m находится на расстоянии r от центра однородного шара радиуса R и массы M за его пределами. Силу взаимодействия можно определить, пользуясь предыдущими результатами. Для этого выделим в шаре сферический слой радиуса x и толщины dx с центром в центре шара. Масса выделенного слоя равна:
dM = |
M |
dV = |
3M 4πx2 |
dx = |
3Mx2 dx |
|
V |
4πR3 |
R3 |
||||
|
|
|
По (231) сила взаимодействия точки с выделенным слоем равна:
dF = − |
γmdM |
= − |
γm 3Mx2 dx |
|
r2 |
r2 R3 |
|
||
|
|
|
||
Интегрируя, получаем силу взаимодействия точки с шаром: |
|
|||
|
R |
|
|
|
F = ∫dF = − γmM |
(232) |
|||
|
0 |
|
r2 |
|
|
|
|
|
|
Если же точка находится внутри шара, надо учитывать взаимодействие только со слоями шара, с внутренними по отношению к точке:
F = − |
γmM |
вн |
(233) |
r2 |
|
||
|
|
|
где: Mвн - суммарная масса внутренних слоев шара, равная:
|
|
= |
3γmM 4πr3 |
r3 |
||||
M |
вн |
|
|
|
= M |
|
|
|
|
|
|
|
|
||||
|
|
r2 R |
3 |
3 |
R3 |
|||
|
|
|
||||||
Отсюда сила взаимодействия равна: |
|
|
|
|
|
|
||
|
|
|
F = − γmM r |
(234) |
||||
|
|
|
|
|
R3 |
|
|
|
13.Работа и энергия.
13.1.Работа силы, работа суммы сил.
Работой силы называют величину, равную произведение силы на перемещение точки приложения силы:
A = F s |
(235) |
Как видно, если сила и перемещение взаимно перпендикулярны, работа силы равна нулю. Например, центростремительная сила не производит работы, ее роль сводится лишь к искривлению траектории.
Работа суммы сил равна сумме работ, производимых отдельными силами системы.
Например:
A = F ds = (Fx ex + Fy ey + Fz ez )(dxex + dyey + dzez )= Fx dx + Fy dy + Fz dz (236)
13.2Частные случаи вычисления работы.
13.2.1.Работа силы тяжести.
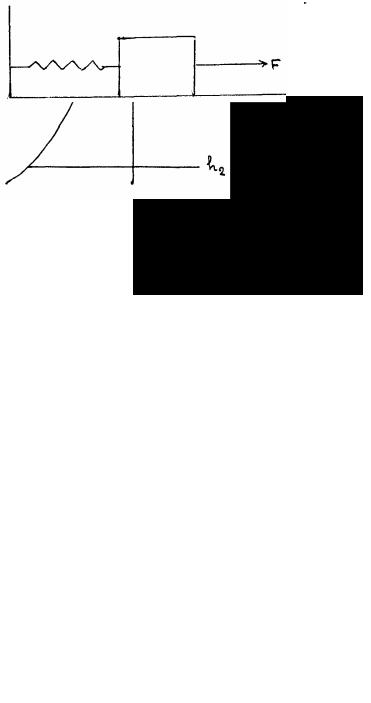
Рис.54 Пусть тело под действием силы тяжести скользит по наклонной поверхности произвольной
формы (рис.54.) работа нормальной реакции по (235) равна нулю, поэтому при отсутствии трения работу совершает только сила тяжести. На элементарном перемещении работа ds силы равна:
dA = mgds cosα = mgdh |
(237) |
Следовательно, на конечном перемещении работа сил тяжести не зависит от формы траектории и равна:
h1
A = ∫mgdh = mg h
h2
где: h = h1 − h2 перемещение тела по вертикали.
13.2.2.Работа упругих сил.
На гладкой горизонтальной плоскости находится тело, скрепленное пружиной жесткости k с вертикальной стенкой (рис.55).
|
|
|
|
|
|
|
Рис.55 |
||
Если под |
действие внешней силы F пружина |
растягивается на x , возникает сила |
||
упругости |
пружины, равная в пределах упругих |
деформаций Fупр = −kx . Элементарная |
||
работа упругих сил по перемещению тела из этого положения на dx равна: dA = −kxdx
Работа же силы на конечном перемещении:
x |
kx |
2 |
|
A = ∫dA = − |
|
(238) |
|
2 |
|
||
0 |
|
|
|
|
|
|
где x – растяжение (удлинение) пружины.

13.3.Работа и кинетическая энергия.
Если на тело массы m действует постоянная сила F , работа ее на перемещении s :
A = mvк2 − mvн2
22
т.е. равна разности кинетических энергий тела в конце и в начале перемещения. Аналогичный результат можно получить и для переменной силы. Для этого разобьем все перемещение на малые участки, в пределах которых силу можно считать постоянной и ее работу вычислить по (239):
|
A = |
mv2 |
|
|
− |
mv |
2 |
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
0 |
|
, |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
A = |
|
|
mv2 |
|
|
− |
|
|
mv2 |
|
|
|
|||||
|
2 |
|
|
|
|
|
|
1 |
|
|
, |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
A = |
mvn2 |
|
|
− |
mvn2−1 |
|
|||||||||||
|
n |
2 |
|
|
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
На всем перемещении работа силы равна: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A = ∑ Ai = |
mvn2 |
|
|
|
− |
mv02 |
|
(240) |
|||||||||
|
|
|
|
|
||||||||||||||
|
i |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|||||
Если же на тело действуют дополнительно силы трения, получаем:
A1 = (F − Fтр ) s = A − Aтр |
= |
mv2 |
− |
mv02 |
= Ek |
(241) |
|
|
|||||
|
2 |
2 |
|
|
||
где: ν и ν 0 - скорость тела в конце и в начале перемещения, А mp - работа сил трения. Следовательно, работа силы F равна:
A = Ek + Aтр |
(242) |
13.4. Работа центральных сил.
Рис.56
Если на тело действует центральная сила F (рис.56), ее работа на элементарном перемещении dr вдоль линии действия силы равна (вдоль траектории1):
dA = Fr dr |
(243) |
|||
а работа на конечном перемещении: |
∫ |
|
|
|
A = |
Fr dr |
(244) |
||
|
||||
При движении по произвольной траектории на элементарном перемещении работа силы выражается соотношением:
dA = Fr ds cosα = Fr dr

т.е. совпадает с (243). Т.е. работа центральных сил не зависит от формы траектории, а определяется лишь начальным и конечным положениями перемещаемого тела.
Силы, работа которых не зависит от формы траектории, называют консервативными. К ним, например, относятся силы упругости, силы электростатического взаимодействия между точечными зарядами, гравитационные силы, а силы трения – не являются консервативными.
13.5 Потенциальная энергия.
Потенциальной энергией называют энергию, определяемую конфигурацией системы, относительным расположением отдельных взаимодействующих тел. выражение для потенциальной энергии для произвольного взаимодействия записать сложно, обычно определяют ее изменение относительно уровня, условно принятого за нулевой. Например, потенциальная энергия тела массы m в поле тяготения Земли, находящегося на высоте h
над ее поверхностью:
γmM Ep = − +
R h
а на поверхности:
Ep0 = − γmM R
Изменение потенциальной энергии тела относительно поверхности Земли:
Ep' = Ep − Ep0 = |
γmMh |
(225) |
R(R + h) |
При r « R (225) принимает вид:
E'p = γmMh = mgh R2
Таким выражением и пользуются, как правило, при расчетах. Здесь потенциальная энергия отсчитывается от определенного уровня (поверхности Земли), на которой она условно принята нулевой.
Такой подход оправдан тем, что при изменениях конфигурации систем изменение состояния определяется не самим значением потенциальной энергии, а только изменением ее.
13.6. Нормировка потенциальной энергии, закон сохранения энергии.
Положим, что в замкнутой консервативной системе выделены состояния 1, 2 и 3, условно принятое за исходное. При переходе из состояний 1, 2 в исходное (рис. 57) работа консервативных сил равна:
(рис. 57)
A10 = Ek0 − Ek1 (246)
A20 = Ek 0 − Ek2 (247)
откуда:
A10 + Ek1 = A20 + Ek 2 |
(248) |
Т.е. для любых состояний системы кинетическая энергия в этом состоянии и работа внутренних сил по переходу из выбранного состояния в исходное - величина постоянная для всех состояний системы. При этом знак работы определяется выбором исходного состояния. Для расчетов важно, чтобы работа сил на любом переходе имела одинаковый знак, поэтому в выражении (248) к значению работы надо добавить такую положительную величину a , чтобы:
A10 + a > 0,
A20 + a > 0.
Сама проделанная операция выбора a называется нормировкой потенциальной энергии, а
сумма Ai0 + a - потенциальной энергией |
системы |
в данном состоянии. С учетом |
сказанного: |
|
|
Ep + Ek |
= const |
(249) |
для всех состояний системы. Это и есть закон сохранения механической энергии. Пример нормировки приведен в предыдущем параграфе.
14. Динамика твёрдого тела.
Абсолютно твердым телом называют абсолютно неизменяемую систему точек, отдельных частиц тела, поэтому к абсолютно твердому телу можно применить уже описанные законы динамики системы точек при условии ее неизменяемости.
14.1.Момент инерции твёрдого тела.
Для описания вращательного движения тела существенно значение его момента инерции. По определению момент инерции твердого тела равен сумме моментов инерции отдельных его частиц:
I = ∑mi ri2
i
где mi - масса i -й частицы тела, ri - ее расстояние от заданного центра или оси.
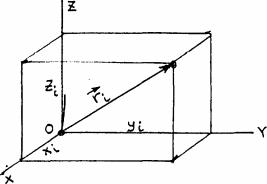
Предположим, что масса выделенной частицы тела mi , расстояние от |
нее до начала |
|||
координат (т. о) ri , а координаты, соответственно, xi , yi , zi (рис. 58). |
|
|||
Момент инерции относительно т. О по определению равен |
|
|||
I0 = ∑mi ri |
2 |
|
|
(250) |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 58) |
|
а относительно координатных осей: |
|
Ix = ∑mi (yi2 + zi2 ) |
(251) |
i |
|

I y |
= ∑mi (xi2 |
+ zi2 ) |
(252) |
|
i |
|
|
Iz |
= ∑mi (xi2 |
+ yi2 ) |
(253) |
|
i |
|
|
Сравнивая (230), (231), (232) и (233), получим связь момента инерции тела относительно начала координат с моментами инерции относительно координатных осей:
I0 |
= |
1 |
[Ix + I y + Iz ] |
(254) |
|
||||
|
2 |
|
|
|
Если одним из размеров тела можно пренебречь по сравнению с двумя другими (плоское тело), эта связь запишется в виде
I0 = Ix + I y |
(255) |
14.2.Примеры расчёта сил инерции.
14.2.1Момент инерции тонкого стержня относительно оси, перпендикулярной стержню и проходящий через его центр масс.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 59) |
|
|
|
|
|
|
Если стержень имеет массу m и длину l , а ось |
z проходит |
через центр масс стержня |
|||||||||||||||
(рис. 59), то координаты левого и правого концов стержня равны - − |
l |
и |
l |
. Выделим в |
|||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
||
стержне на расстоянии x от оси малый его участок длины |
dx . Его момент инерции |
||||||||||||||||
относительно z равен: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dI |
|
= |
m |
x2 dx |
|
|
(256) |
|||||||||
|
z |
|
|
|
|||||||||||||
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегрируя (236), получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
ml2 |
|
|
|
|
|
|
|
|
I |
|
= |
2 |
dI |
|
= |
|
|
|
(257) |
||||||
|
z |
∫ |
z |
|
|
|
|||||||||||
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
− l |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
14.2.2.Момент инерции тонкой пластины прямоугольной формы относительно одной из её сторон.
(рис. 60)
Размеры тонкой пластины массы m приведены на рис. 60, выделим в пластине на расстоянии x от оси z узкий слой ширины dx и запишем его момент инерции:

dI |
|
= |
m |
x2bdx = |
m |
x2 dx |
(258) |
z |
|
|
|||||
|
|
ab |
|
a |
|
||
|
|
|
|
|
|||
Интегрируя (258), получаем: |
|
|
|
|
|
|
|
|
|
I |
|
= a |
dI = |
ma3 |
|
|
(259) |
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
z |
|
∫ |
|
|
z |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
14.2.2 Момент инерции однородного шара относительно его центра. |
|||||||||||||||
Пусть масса шара равна m , а радиус |
R . Выделим в шаре тонкий сферический слой |
||||||||||||||
радиуса x , толщины dx , момент инерции которого относительно центра шара равен |
|
||||||||||||||
dI |
0 |
= dm x2 |
|
|
|
|
|
|
|
|
|
(260) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dm = |
3m |
|
4πx2 dx = |
3m |
|
x2 dx |
|
||||||||
4πR3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
R3 |
|
|
|
||||
Интегрируя (260), получим искомый результат: |
|
|
|
|
|
|
|
|
|||||||
|
|
R |
|
|
3m R |
|
|
|
|
3 |
|
|
|||
I0 = ∫dI0 |
|
= |
|
|
∫ x4 dx = |
|
|
mR2 |
(261) |
||||||
|
R |
3 |
|
5 |
|||||||||||
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
||
14.3. Теорема Штейнера.
Расчет моментов инерции тела даже правильной формы, если ось не проходит через центр масс тела, затруднен. В этом случае удобно пользоваться теоремой Штейнера:
Момент инерции тела относительно произвольной оси z' равен сумме момента инерции относительно оси z , параллельной заданной и проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями:
Для доказательства через центр масс тела (т. С) проведем ось z , параллельную заданной
оси z' (рис. 61). Расстояние между осями равно |
a . Выберем частицу тела массы mi , |
||||
настояние от нее до осей z и z' |
указаны на рисунке. |
|
|||
Момент инерции тела относительно z' по определению: |
|
||||
|
Iz' |
= ∑mi r'i2 |
|
|
(262) |
|
|
i |
|
|
|
Из геометрических соображений: |
|
|
|
|
|
Iz' = ∑mi (ri |
2 + a2 − 2ri a cosαi )= ∑mi ri |
2 |
+ ∑mi a2 |
− 2∑mi ri cosαi |
|
i |
|
i |
|
i |
i |
Первое слагаемое в правой части дает момент инерции тела относительно z :
Iz = ∑mi ri |
2 |
(263) |
i |
|
|

Поскольку a=const, второе слагаемое принимает вид (Ma2), где М - масса тела. В последнем слагаемом:
2∑mi ri a cosαi = 2a∑mi xi
i |
i |
следовательно, по определению центра масс:
∑mi xi
xC = i
M
последнее слагаемое обращается в нуль, поэтому:
Iz' = Iz + Ma2
что и требовалось доказать.
14.4. Кинетическая энергия твёрдого тела для различных типов движения.
1. Поступательное движение
Ek |
= ∑ |
mivi2 |
= ∑ |
mivC2 |
= |
MvC2 |
|
(264) |
|||||
|
|
|
|
||||||||||
|
|
i |
2 |
|
i |
2 |
2 |
|
|
|
|||
2. Вращательное движение |
|
||||||||||||
Ek |
= |
1 |
∑mivi2 |
= ∑mi ri |
2ω 2 = |
Iω 2 |
(265) |
||||||
|
|
||||||||||||
|
2 |
|
i |
|
|
i |
2 |
|
|||||
3.Плоское движение тела
Влюбой момент времени плоское движение можно представить, как вращение вокруг мгновенного центра вращения, пусть О -мгновенный центр вращения, а т. С - центр с масс тела. Тогда:
|
|
|
I |
ω 2 |
|
I |
C |
+ Ma2 |
|
I |
C |
ω 2 |
Mv2 |
|
|
E |
|
= |
0 |
|
= |
|
|
ω 2 = |
|
|
+ |
C |
(266) |
||
k |
|
2 |
|
|
2 |
|
2 |
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
где: IC и I0 - моменты инерции тела относительно осей, проходящих через центр масс и
мгновенный центр вращения, |
a |
- расстояние между осями, vC . - скорость центра масс |
поступательной части движения), |
ω (омега) - угловая скорость вращения вокруг оси, |
|
проходящей через центр масс. |
|
|
СВОБОДНЫЕ ОСИ ВРАЩЕНИЯ
Момент импульса тела в произвольном случае его вращения не совпадает по направлению с вектором угловой скорости вращения. Тем не менее, существует такие оси, при вращении вокруг которых момент импульса и угловая скорость по направлению совпадают. Такие оси называются главными осями инерции (свободными осями вращения). Таких осей в каждом теле три, все они взаимноперпендикулярны и проходят через центр масс тела, поэтому их удобно принимать в качестве системы отсчета для каждой из этих осей
Nx = Ixωx , N y = I yω y , Nz = Izωz .
В случае произвольного по форме тела легко показать, что N и ω (омега) не совпадает по направлению (рис. 62).
Кинетическая энергия тела при таком вращении может быть представлена суммой энергий вращения вокруг трех главных осей:
Ek |
= |
1 |
(Ixωx2 + I yω y2 + Iωz2 ) |
|||||||||
|
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
||
или: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
N 2 |
|
N y2 |
|
N 2 |
|
||
E = |
|
|
|
x |
+ |
|
+ |
z |
|
|||
|
|
|
|
|
||||||||
|
k |
|
|
|
|
Ix |
|
I y |
|
Iz |
|
|
|
|
|
2 |
|
|
|
||||||

или:
|
|
Ek = |
1 |
|
(Nxωx + Nyω y + Nzωz ) |
|||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
или: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
= |
1 |
N ω |
||
|
|
|
|
|
|
|
|
|
k |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Направление векторов N |
|
и ω |
|
можно |
указать заданием направляющих косинусов, |
|||||||||||
например: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosα |
|
= |
|
Nx |
|
= |
|
|
|
|
|
|
Ixωx |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
N |
|
|
|
|
|
(Ixωx )2 + (I yω y )2 + (Izωz )2 |
||||||
|
|
|
|
|
|
|
|
|
||||||||
cosα |
|
= |
|
ωx |
||
2 |
|
|
ω |
|
||
|
|
|||||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
очевидно, что направления N |
и ω |
|||||
Ix = I y |
= Iz |
|||||
= |
|
ωx |
|
|
|
(ωx )2 + (ω y )2 + (ωz )2 |
совпадают в том случае, если: = I (267)
Твердое тело, отвечающее условию (267), называется шаровым волчком. Твердое тело, у которого Ix = Iy = I ≠ Iz , называется симметричным волчком с осью симметрии z . Твердое тело, у которого все три главных момента инерции различны, называет несимметричным волчком Ix ≠ I y ≠ Iz .
СВОБОДНОЕ ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
Свободным называют такое вращение тела, при котором сумма моментов внешних сил, приложенных к телу, равна нулю:
∑M = 0
Отсюда следует, что при свободном вращении:
Ek = const, N = const
Рассмотрим свободное вращение симметричного волчка с осью симметрии z .Кинетическая энергия для него равна:
|
1 |
|
2 |
E = |
|
Nx |
|
|
|
||
k |
2 |
|
Ix |
|
|
|
N y2 |
|
N 2 |
|
1 Nx2 |
+ N y2 + Nz2 |
|
1 |
|
1 |
|
|
|
|
|||
+ |
|
+ |
z |
|
= |
|
|
|
|
+ |
|
− |
|
N 2 |
|
= const |
|
|
|
|
|
|
|
|
|
||||||||||
|
I y |
|
Iz |
|
|
2 |
I |
|
Iz |
|
I |
|
z |
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В этом выражении первое слагаемое постоянно, следовательно, постоянно и второе, т.е.:
Nz = const |
(268) |
Учитывая, что Nz = Izωz получаем: |
|
ωz = const |
(269) |
Написав выражение для кинетической энергии в виде:
Ek |
= |
1 |
(Ixωx2 + I yω y2 |
+ Iωz2 )= |
1 |
[I(ωx2 + ω y2 + ωz2 )+ (Iz |
− I )ωz2 ]= const |
||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
2 |
|
|
|
|
|
2 |
|
|
||||||||||||||
делаем вывод, что: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
= const |
(270) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
наконец, кинетическую энергию представим в виде: |
|
||||||||||||||||||||||
|
|
|
E |
k |
= |
1 |
N ω = |
1 |
|
|
N |
|
|
|
ω |
|
cosα = const |
(271) |
|||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где α - угол между векторами N и ω .Из (271) следует, что, |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
α = const |
(272) |
||||||||||
Учитывая (269), (270), (271) ,(272) свободное вращение тела можем представить как вращение оси симметрии тела вокруг неподвижного направления N . При этом
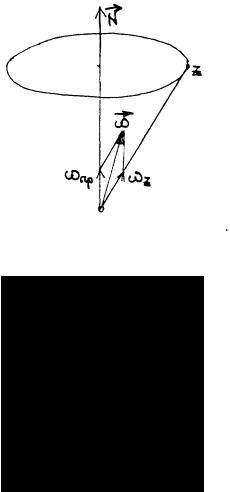
относительное расположение ω , N и Z со временем сохраняется (рис.53). Такое вращение при отсутствии моментов внешних сил называется регулярной прецессией. Тело вращается вокруг оси симметрии со скоростью ωz , a сама ось описывает коническую
поверхность, вращаясь вокруг неподвижного направления N с угловой скоростью прецессии ω р .
(рис. 63)
Т. o. для вращающегося тела можно выделить три оси - момента импульса, угловой скорости и оси симметрии. Существенно, что относительное расположение этих осей зависит от величины угловой скорости вращения тела вокруг оси симметрии ω я . Несложно
доказать, что при очень быстром вращении тела (ω я >> ωпр ) все три направления
практически сливаются в одно. Эта особенность быстро вращающихся тел лежит в основе элементарной теории гироскопов.
