Lektsii_Mekhanika_Ch_1

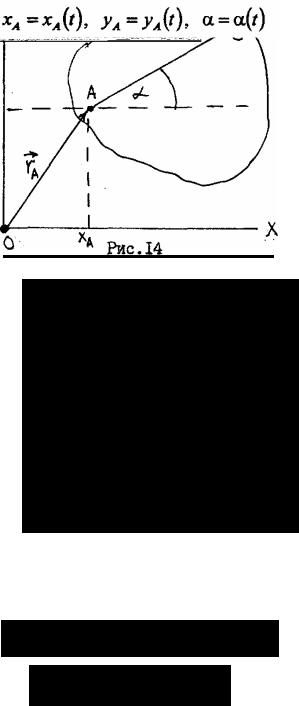
любой другой нормали. Поэтому для изучения плоского движения тела достаточно рассмотреть движение его сечения плоскостью, параллельной заданной, т.е. решить задачу кинематики в плоской системе координат.

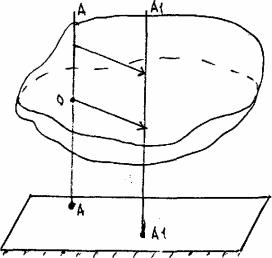рис 13

Для определения положения сечения в пространстве в любой момент времени необходимо прежде всего задать положение произвольной точки А (полюса) этого сечения векторным или координатным способом. Кроме того, необходимо провести в сечении произвольную прямую АВ и указать угол a (альфа), который она образует с одной из осей координат (рис. 14). Движение сечения считается

заданным, если для любого момента времени известны зависимости:

(29)

или

(28)

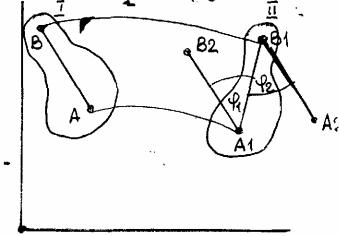рис 15 Соотношения (28), (29) задают кинематический закон плоского движения тела в векторном и координатном виде соответственно.

Осуществим плоское перемещение тела (его сечения) из положения 1 в положение 2 (рис. 15). В сечении выберем произвольную прямую AB. Выберем также в качестве полюса точку А. Если переместить сечение поступательно вместе с полюсом А, то полюс займет положение A1, а прямая АB - положение A1B2. Для приведения сечения в конечное положение 2 его необходимо повернуть вокруг полюса на угол ϕ1. Таким образом, плоское перемещение тела можно рассматривать как одновременно происходящие поступательное перемещение вместе с полюсом и вращение вокруг этого полюса.

Если выбрать в качестве полюса точку B то после поступательного перемещения вместе с ним прямая AB займет положение A2B1. Для совмещения сечения с его конечным положением 2 его надо повернуть на угол ϕ2. Следовательно, и в этом случае плоское перемещение можно представить как одновременно происходящие поступательное перемещение вместе с полюсом и вращение вокруг него. Очевидно, что и направление, и угол поворота в обоих случаях совладают. Поэтому кинематические характеристики поступательной части движения зависят от выбора полюса, а вращательной - не зависят.

2.6. СКОРОСТЬ ОТДЕЛЬНЫХ ТОЧЕК ТЕЛА ПРИ ПЛОСКОМ ДВИЖЕНИИ.

Выберем в качестве полюса т. А (рис. 16) и выделим произвольную точку B сечения тела. Положение их в пространстве определим векторным способом (ra и rb соответственно). Кроме того, положение т. В определим, указав радиус-вектор r.

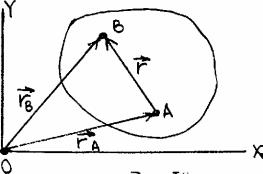рис 16

По определений скорость т. В:

(30)

Таким образом, скорость любой точки тела при плоском движении определяется суммой двух составляющих. Выясним их смысл.

Следовательно, эта составляющая определяет скорость поступательной части движения вместе с

полюсом. Если же в процессе движения(вращение вокруг т. А), скорость точки В равна:

очевидно, что эта составляющая представляет собой линейную скорость вращательной части движения вокруг полюса.

Таким образом, в любой момент времени скорость произвольной точки тела, совершающего плоское движение, определяется векторной суммой скоростей поступательного движения вместе с полюсом и вращательного движения вокруг полюса.

Может оказаться так, что для какой-либо точки тела сумма окажется равной нулю (точка в данный момент времени покоится). Такую точку называют мгновенным центром вращения, и плоское движение тела можно рассматривать в данный момент времени как вращение вокруг мгновенного центра вращения. Примером мгновенного центра может служить точка касания цилиндра с плоскостью, по которой он катится без скольжения.

3.Задачи кинематики.

3.1.ПЕРВАЯ ЗАДАЧА КИНЕМАТИКИ.

Первая задача кинематики состоит в нахождении кинематических характеристик движения по заданному закону движения.

Пример: Закон движения точки задан в координатной форме

(31)

Прежде всего, определим уравнение траектории точки в виде

(32)

Следовательно, траекторией точки является прямая (рис. 17).

(рис. 17)

Прямая ограничена максимальными отклонениями точки от положения равновесия ±А вдоль оси ОХ и ±B вдоль ОY.

Составляющие скорости равны:

(33)

а полная скорость:

(34)

Постоянную интегрирования С2 также получаем из начальных условий:

(45)

следовательно:

(46)

Аналогично получаем для других координатных направлений:

(47)

(48)

Полная скорость равна:

(49)

4.1. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ.

4.1. Сила.

ОПРЕДЕЛЕНИЯ:

Изменение состояния тела происходит в результате взаимодействий, которые приводят к изменению, как внутреннего состояния тел, так и состояния их движения. Количественной мерой взаимодействий, приводящих к изменению состояний тел, является сила.

Сила - векторная величина, она характеризуется следующими элементами: величиной, направлением в пространстве и точкой приложения силы.

Линия, вдоль которой направлена сила, называется линией действия силы. Совокупность сил, приложенных к телу, называют системой сил.

Если под действием системы сил, приложенных к телу, оно может пребывать в состоянии покоя, система называется уравновешенной

Если одну систему сил, приложенных к телу, можно заменить другой, не изменяя его состояние, системы называются эквивалентными.

Сила, эквивалентная системе сил, называется равнодействующей этой системы.

Сила, равная по величине равнодействующей и противоположно ей направленная, называется уравновешивающей.

Силы взаимодействия между телами одной и той же системы называются внутренними. Силы взаимодействия с телами, не входящими в состав данной системы называются внешними.

Силы, приложенные в одной точке тела, называются сосредоточенными.

Силы, приложенные ко всем точкам поверхности или объема тела, называются распределенными.

4.2. СЛОЖЕНИЕ СИЛ И РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ.

Сложение сил - задача нахождения равнодействующей для заданной системы сил. Находить равнодействующую можно аналитически и геометрически. В простом случае системы двух сил (рис. 18) можно аналитически выразить величину равнодействующей силы:

(50)

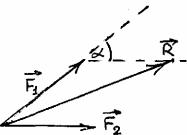(рис 18) где α - угол между направлениями сил системы.

(рис 19)

Рис.19 является частным случаем правила силового многоугольника, по которому описанная операция проводится последовательно для всех сил системы, независимо от их ориентировки в пространстве. Начало вектора равнодействующей совпадает с точкой приложения первой (по построению) силы системы, а конец - с концом вектора последней.

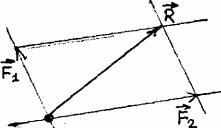(рис 20)

Разложением сил на составляющие называют задачу нахождения системы сил, для которой данная сила является равнодействующей. Например, для искомой системы двух сил задаются направления линий действия сил системы (рис.20). Через начало и конец вектора заданной силы проводят прямые, параллельные указанным направлениям. Искомые силы системы определяются сторонами полученного параллелограмма.

4.3. ПРОЕКЦИИ СИЛЫ НА ПЛОСКОСТЬ И ОСЬ.

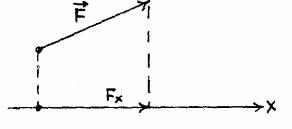
Проекцией силы на плоскость называют вектор Fxy, заключенный между проекциями начала и конца вектора силы на заданную плоскость (рис. 21).

Аналогично - проекцией силы на ось называют отрезок, заключенный между проекциями начала и конца вектора силы на заданную ось (рис. 22).

В отличие от проекции на плоскость, проекция силы на ось является скалярной величиной.

(рис 22)

4.4.Статическое и динамическое проявление сил.

Впроцессе взаимодействия (в результате действия сил) тела изменяют свое внутреннее состояние и (или) состояние движения. В соответствии с этим рассматривают статическое проявление сил (приводящее к изменению внутреннего состояния тел) и динамическое (приводящее к изменению состояния движения). Например, при скольжении тела по наклонной плоскости сила его тяжести проявляется двояким образом: сообщая телу ускорение (динамически) и деформируя его в результате взаимодействия с наклонной плоскостью (статически). Поэтому в самом общем смысле все способы измерения сил можно разделить на два класса - статические и динамические. Пример: пружинный динамометр и акселерометр.

4.5. 1-й ЗАКОН НЬЮТОНА (ЗАКОН ИНЕРЦИИ).

Существуют такие системы отсчета, в которых тело, предоставленное самому себе, может находиться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку действие внешних сил не вынудят его изменить это состояние.

Способность тел сохранять состояние покоя или равномерного и прямолинейного движения, препятствуя внешним воздействиям, называется инертностью. Это – внутреннее свойство, присущее всем телам, независимо от их природы и состояния. Причины же, вызывающие изменения состояния тела, всегда внешние - это силы.

Количественной мерой инертности тел является их масса.

4.6. 2-Й ЗАКОН НЬЮТОНА (ОСНОВНОЙ ЗАКОН ДИНАМИКИ).

Как и все законы динамики основной закон получен опытным путем. В частном случае, когда масса тела в процессе взаимодействий не изменяется, основной закон динамики формулируется в форме: ускорение, получаемое телом в результате действия на него системы сил, прямо пропорционально равнодействующей приложенной системы сил, обратно пропорционально массе тел и направлено вдоль линии действия равнодействующей.

Математическая формулировка частной формы основного закона динамики имеет вид:

(51)

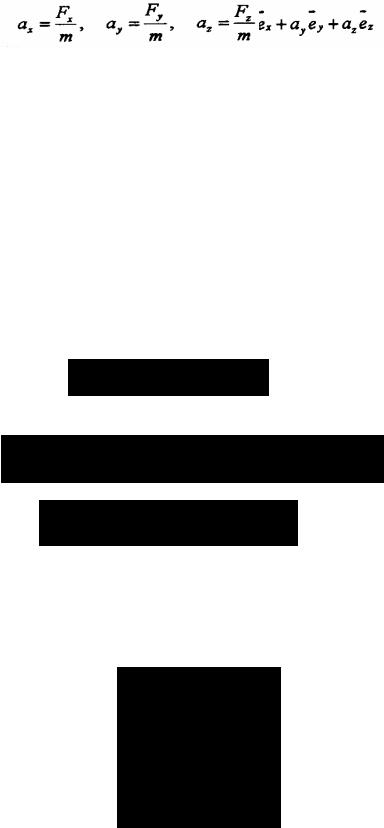
где: F - равнодействующая приложенной системы сил.

Более общей является следующая формулировка основного закона:

Изменение импульса тела пропорционально импульсу равнодействующей приложенной системы сил и направлено вдоль линии действия равнодействующей.

Под импульсом силы понимают произведение силы на время ее действия. Математическая формулировка общей формы основного закона динамики имеет вид:

(52)

4.7. 3-Й ЗАКОН ДИНАМИКИ (ЗАКОН ДЕЙСТВИЯ И ПРОТИВОДЕЙСТВИЯ).

Существует две равноправные формулировки 3-го закона:

1.Действию всегда есть равное и противоположно направленное противодействие

2.Тела действуют друг на друга с силами, равными по величине и противоположно направленными. Эти формулировки получены в результате обобщения экспериментальных фактов, которые свидетельствуют о том, что тела взаимодействуют всегда попарно, т.е. на изолированное тело силы не действуют.

С 3-м законом динамики тесно связан закон сохранения импульса. Действительно, если на два тела действуют только силы взаимодействия между ними, то, по 3-му закону динамики, эти силы равны по величине и противоположно направлены. Следовательно, по основному закону, одинаковы и противоположно направлены изменения импульсов тел, а общий импульс системы тел не изменяется.

4.8.ПРИНЦИП НЕЗАВИСИМОСТИ ДЕЙСТВИЯ СИЛ.

Если на тело действует несколько сил, то каждая из них сообщает телу ускорение, определяемое основным законом динамики, так, как если бы других сил не было.

Например, произвольно направленную и в пространстве силу F можно представить в виде суммы ее составляющих (компонентов):

где ex, ey, ez - орты прямоугольной системы координат OXYZ. Второй закон динамики в этом случае имеет вид:

откуда:

Т. о., в приведенном рассуждении учтен принцип независимости действия сил.

4.9. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОГО ЦЕНТРА.

Моментом силы называют количественную меру вращательного эффекта, вызываемого силой. Момент силы должен определять величину этого эффекта, плоскость поворота точки и направление поворота в этой плоскости.

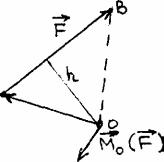(рис 23)

Величина момента силы равна произведению модуля силы на ее плечо h (величину перпендикуляра, опущенного из заданного центра O на линию действия силы). Если начало вектора силы совпадает с точкой А, а конец – А с точкой В, то, очевидно, плоскость поворота совпадает с плоскостью треугольника OAB (рис. 23).

Условились вектор момента силы относительно центра M0(F) проводить из этого центра O перпендикулярно плоскости поворота в ту сторону, откуда поворот виден происходящим против хода часовых стрелок. Модуль же вектора (длина вектора в выбранном масштабе) равен .

Очевидно, что такой вектор равен векторному произведению:

(53)

где: r - радиус-вектор точки приложения силы, проведенный из заданного центра.

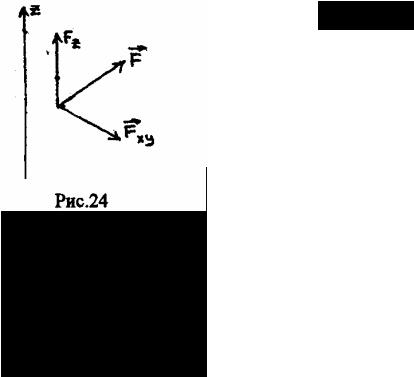
4.10. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ.

Моментом силы относительно оси называют величину, характеризующую вращательный эффект, вызываемый силой при вращении тела вокруг заданной оси.

К телу А, способному вращаться вокруг оси z приложена сила F (рис. 24). Очевидно, что эффект вызываемый силой, определяется суммой эффектов, вызываемых ее проекциями Fz и Fxy, первая из которых вращения тела вокруг оси z вызвать не может. Следовательно, момент силы относительно заданной оси определяется моментом ее проекции на плоскость, перпендикулярную оси, относительно точки Пересечения оси с плоскостью.

4.11. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО КООРДИНАТНОЙ ОСИ.

Пользуясь полученным выше результатом можно записать выражения моментов силы относительно координатных осей. Пусть к телу приложена сила F, координаты точки приложения которой равны x,y,z. Момент силы F относительно оси oz равен моменту ее проекции Fxy относительно начала координат (т. 0). В свою очередь момент Fxy равен сумме моментов сил Fx и Fy относительно того же центра. Очевидно, что плечи сил Fx и Fy численно равны координатам точки приложения силы y и x соответственно. С учетом знаков моментов этих составляющих можно записать

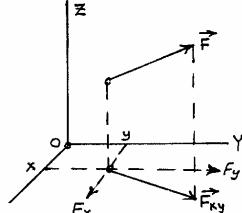(рис 25)

(54)

Аналогично определяются моменты силы F относительно осей ОХ и ОУ:

(55)

(56)

4.12. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА И КООРДИНАТНЫХ ОСЕЙ.

Количественной мерой движения при вращении является момент количества движения (момент импульса). По аналогии с моментом силы момент импульса относительно центра и координатных осей записываются в виде:

(57)

(58)

(59)

(60)

2. Основной закон динамики. Уравнение моментов для тела движущего по окружности

Пусть точка движется по окружности радиуса с центром в т. О под действием силы F, составляющей угол α с касательной а окружности (рис. 26).

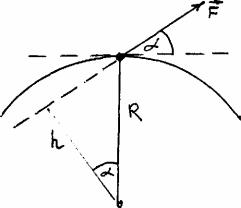(рис 26)