Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lektsii_Mekhanika_Ch_1

.pdf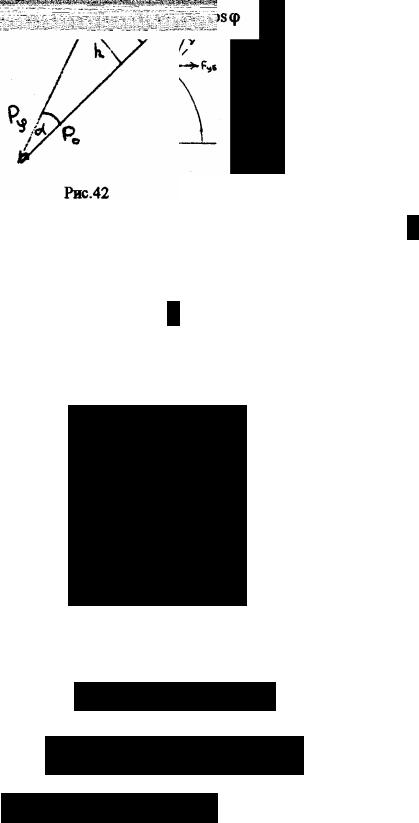

Скачиваний:

Добавлен:

29.02.2016

Размер:

1.41 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

9.4. Зависимость веса тел от географической широты местности.

Географической широтой местности называют угол между радиусом Земли, проведенным в рассматриваемую точку и экваториальной плоскостью (рис. 41).

На тело, покоящееся относительно Земли, действует сила гравитационного

Притяжения P0 , направленная к центру Земли, и реакция поверхности .

Реакция отклоняется от нормали к поверхности на угол α, чтобы равнодействующая

реакции поверхности Земли R и гравитационной силы P0 давала центростремительную силу, обеспечивающую нормальное ускорение при вращении тела вместе с поверхностью Земли.

Силу, равную по величине реакции	и противоположно ей направленную,

называют весом тела Pϕ .

В системе, связанной с Землей, тело покоится, поэтому необходимо ввести центробежную силу инерции .

Из силового треугольника, представленного на рис.42, можно определить величину веса тела на географической широте ϕ и угол отклонения α силы веса тела от радиуса Земли.

Центробежная сила инерции равна:

(185)

С учетом этого получим:

т.е

(186)

Так как угол α мал, а m = P0 , получим окончательно: g0

(187)

Угол отклонения α легко определить из рис. 42.

(188)

Как видно из (167) и (168), вес тела максимален на полюсах и минимален на экваторе. Отклонение силы веса от радиуса Земли максимально на широте π/4 и равно нулю на полюсах и экваторе.

10.Силы трения. Сухое трение.

10.1.Силы трения скольжения.

Сухим (внешним) трением называют силы сопротивления движению, возникающие при относительном движении одного твердого тела по поверхности другого. Силы сопротивления движению определяются наличием микро- и макронеровностей поверхностей трущихся тел и взаимодействием между ними. При скольжении одной твердой поверхности по другой в плоскости соприкосновения тел возникают силы, направленные противоположно относительной скорости. Эти силы и называют силами трения скольжения. Основные законы и закономерности для сил трения скольжения получены опытным путем. Закон Кулона определяет величину сил трения скольжения:

Fтр = kN

(189)

где: Fтр - сила трения скольжения, N - нормальная составляющая реакции поверхности, k - коэффициент трения скольжения.

Коэффициент трения скольжения k является безразмерной величиной и определяется природой и состоянием поверхностей трущихся тел.

Кроме закона Кулона опытным путем установлен ряд закономерностей для трения скольжения среди которых наиболее часто употребляются следующие:

1.При попытке сдвинуть одно тело по поверхности другого в плоскости контакта возникают силы, сопротивления, изменяющиеся от нуля до предельного значения, называемого силой трения покоя.

2.С увеличением относительной скорости трущихся тел силы - трения сначала убывает, а затем начинают возрастать.

3.Силы трения тем меньше, чем тверже трущиеся поверхности.

10.2. Силы трения качения.

Трение качения возникает при качении одного твердого тела по поверхности другого. При попытке сдвинуть тело по поверхности другого в плоскости соприкосновения возникает

сила		препятствующая этому (рис. 43).
сила	F	препятствующая этому (рис. 43).
	τ
	τ

Положим, что оба тела являются абсолютно твердыми, недеформируемыми, В этом случае

нормальная составляющая реакции N проходит через точку касания и центр масс катка (считаем его однородным симметричным телом, например, цилиндром). При такой модели любая по величине сила может вызвать качение катка, т.е. сопротивление движению.

не возникает. Более того, сила Fτ должна вызывать угловое ускорение при любой по

величине силе Fτ , что противоречит опыту.

Сопротивление качению может возникать в том случае, если нормальная реакция смещается относительно вертикального диаметра катка в сторону движения. Это происходит в том случае, если давление катка на поверхность будет не в точке, а по участку поверхности, а интенсивность давления будет больше впереди вертикального диаметра катка, как показано на рис. 44.

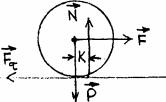Рис.44 Следовательно, поверхность должна деформироваться, причем деформации будут несимметричными относительно вертикального диаметра.

Положим, что сила F вызывает равномерное качение катка, т.е.

FR = kN

Откуда

F =	k	N	(190)

	R

Здесь k (коэффициент трения качения) является размерной величиной. Смысл его- ''плечо'' нормальной составляющей реакции поверхности.

				10.3. Вязкое трение
	Вязкое трение возникает при			относительном движении слоёв жидкости или газа.
Основные законы вязкого трения получены опытным путём.
Ньютон установил, что если под действием силы площадка P площади S								движется
равномерно		со	скоростью	ν	относительно	площадки	P1	(рис.45),

Рис.45 На подвижную площадку действуют силы сопротивления движению (силы вязкого трения):

F = µS ν

(191)

тр	h

где h - расстояние между площадками (слоями), µ - коэффициент вязкого трения определяемая свойствами вязкой среды, заполняющей промежуток между площадками.

При движении тел в вязкой среде на них действуют силы сопротивления движению.

Стокс получил выражение для этих сил. При малых скоростях.

F	=	1	C		ρSν 2	(192)

ст	2			x
где: Fст - стоксова сила сопротивления,			ρ - плотность			среды, ν - скорость тела, Сx -

коэффициент, определяемый геометрией тела, S - площадь проекции тела на плоскость, перпендикулярную направлению движения.

10.4. Движение тел в сопротивляющейся среде.

При достаточно больших скоростях тел (или если форма тела является плохо обтекаемой) силы Стокса становятся пропорциональны квадрату скорости:

ρSν 2

(193)

Положим, что тело начинает падать под действием силы тяжести в

сопротивляющейся среде. Пренебрегая силой Архимеда, запишем:

dν

= mg −

ρSν 2

(194)

С течением времени скорость тела возрастает, возрастает и сила Стокса. Наконец, силы тяжести и Стокса уравновешиваются, после чего начинается равномерное движение тела с установившейся скоростью ν 0 . Определим зависимость скорости от проходимого телом пути и значение установившейся скорости. Для этого сначала преобразуем (194):

νdν

ρS

= mg

−

ρSν 2 = mg 1

−

ν 2

2mg

Обозначим:

mg = P,

= a2

Cx ρS

Тогда:

νdν

= g

−ν 2

Или:

νdν

−ν

Интегрируя (195), получим:

−

ln(a2 −ν 2 )=

+ C

Константу интегрирования находим из начальных условий (x=0 и ν =0):

C = −

ln a2

Подставив (197) в (196) получим

2gx

−ν 2

Или:

−ν

−

2gx

= e

Откуда:

−

2gx

ν = a

1− e

(195)

(196)

(197)

(198)

Через достаточно большой промежуток времени (t → ∞ ) скорость тела перестаёт изменяться. Следовательно, значение установившейся скорости равно

ν 0 = 0

(199)

(178)и (179) и дают искомое решение поставленной задачи.

11.Упругость.

11.1 Упругие силы.

Упругостью называют свойство восстанавливать временно утраченную форму и объём, а деформациямисамо изменение формы и объёма тела. Причиной упругости является наличие одновременно присутствующих сил взаимодействия между частицами тела-

притяжения ( −	a1		) и отталкивания ( −	a2		). Равнодействующая этих сил равна:
притяжения ( −	r	n	) и отталкивания ( −	n		). Равнодействующая этих сил равна:
		n		n
		1		r 2
			F = −		a1		+	a2	(200)
			F = −				+	n	(200)
					r	n		n
					r	1		r 2

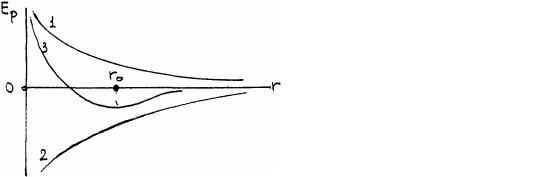
На рис.46 представлены графики силы взаимного отталкивания (1), притяжения (2) и

равнодействующая этих сил (3). На расстоянии r0

между взаимодействующими частицами

равнодействующая равна нулю (положение равновесия). При

r < r0 преобладают силы

отталкивания, а при r > r0 силы притяжения.

Потенциальная энергия взаимодействия на расстоянии r

между частицами:

∞

Ep =

∫

Fdx =

∫

−

dx =

(201)

n1 −1

n2 −1

где:

A =

B =

n −1

−1

Графики потенциальной энергии сил отталкивания (1), притяжения (2) и равнодействующей (3) представлены на рис.47:



Рис.46		Рис.47

11.2. Продольное сжатие и растяжение. Закон Гука.

При продольном сжатии или растяжении одного упругого образца длинны l и площади сечения S удлинение образца l определяется из опыта выражением:

Ps = Eεl

			l = kl	F	(202)
			l = kl	S	(202)
				S
где k - коэффициент упругости, определяемый свойствами материала образца.
Величина ε		= l	называется относительной деформацией. Величина		E =	1	, обратная
Величина ε	l	= l	называется относительной деформацией. Величина		E =		, обратная
	l	l				k
		l				k

коэффициенту упругости, называется модулем упругости Юнга.

С учётом этих обозначений закон Гука для деформации продольного сжатия или растяжения имеет вид:

(203) где Ps - называется напряжением (отношение упругих сил в деформированном образце к площади его поперечного сечения).

При изменении продольных размеров одновременно и поперечные. Изменение d диаметра d образца (однородного цилиндра) также подчиняется закону Гука:

= d = −β

(204)

где: β -коэффициент поперечного сжатия при продольном растяжении.

Сравнивая (203) и (204) получим:

= −

(205)

Величина

σ =

называется

коэффициентом

Пуассона.

Рис.48

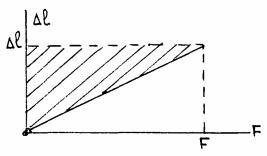
Если деформирующая сила изменяется от нуля до F , абсолютная деформация изменяется, соответственно, от нуля до l то образец приобретает потенциальную энергию упругих деформаций, численно равную работе деформирующей силы. Эта работа равна площади заштрихованной фигуры (рис.48), т.е:

Используя закон Гука, получим:

1SE lε1

Eε

12V

(206)

А плотность энергии, соответственно:

Eε 2

(207)

11.3 Деформация сдвига.

Деформация сдвига возникает при действии на тело касательных усилий (рис. 49). Если к верхней грани образца, имеющего форму параллелепипеда, приложена касательная сила F , распределённая по грани площади S , грань сдвигается на расстояние a , которое

называется абсолютной деформацией при сдвиге.

Рис.49

Относительной деформацией называют отношение абсолютной деформации a к поперечным размерам h . Для сдвига закон Гука принимает форму:

ε =	a	= tgα = n	F	(208)
	h		S

где n -коэффициент сдвига, определяемый свойствами материала образца, величина, обратная n , называется модулем сдвига:

N = 1 n

Поскольку упругие деформации, для которых формулируется закон Гука, имеют место только при маленьких значениях деформации, закон Гука для сдвига принимает вид:

Ps = Nε = Nα	(209)
11.4. Деформация кручения.
Деформации кручения возникают при закручивании одного	основания образца

относительно другого .
относительно другого .
По закону Гука для этого типа деформации
	ε = ϕ = cM	(210)
	L

где ϕ - угол закручивания, L - длинна образца, M - момент закручивающих сил, c - коэффициент кручения.

Величина f = 1 называется модулем кручения т. е. c

ϕ =	M	(211)

L f

Одновременно с закручиванием образца происходит сдвиг его слоёв. Угол сдвига γ определяется из закона Гука.

γ =	Ps	(212)
	N

Угол сдвига можно получить и из чисто геометрических соображений:

γ	= ρϕ		(213)
		L
Сравнивая (212) и (213), получим
P	= ρϕN		(214)
s		L
		L

Момент распределённых сил, приложенных к нижнему основанию образца, получим, используя (214).

Рис.51 Из рис.51 видно, что элементарный момент закручивающих сил, приложенных к элементу основания, равен:

dM	= dF ρ = P dS ρ =				ρ 2ϕN		ρdρdθ =		ρ 3ϕN	dρdθ	(215)
dM	= dF ρ = P dS ρ =						ρdρdθ =			dρdθ	(215)
	s				L				L
					L				L
Полный момент:
	R 2π					πNR4		ϕ
	M = ∫ ∫dM =							L			(216)
	0	0					2	L
	0	0
Сравнивая (210) и (216), получаем связь между модулями сдвига и кручения:
		f	=	πNR4							(217)
		f	=	2							(217)
				2

12.Силы тяготения.

12.1Закон всемирного тяготения.

Закон всемирного тяготения получен Ньютоном из наблюдений видимого движения планет Солнечной системы, используя законы динамики. В векторной форме закон всемирного тяготения, определяющий силы гравитационного взаимодействия, имеет вид:

F = −	γmM r	(218)
	3

где M - масса источника гравитационного поля, m - величина пробной массы, r -радиус- вектор точечной пробной массы относительно центра масс источника поля, γ -

гравитационная постоянная.

Силовой характер поля источника является сила, действующая на единичную пробную массу, помещённую в данную точку поля. Эта величина называется напряжённостью поля:

Eгр = −	γM r			(219)
		r	3
		r

Следует отметить, что закон всемирного тяготения справедлив только для точечных взаимодействующих масс. Кроме того, массы тел, фигурирующие в законе всемирного тяготения, имею другой смысл, нежели в законах динамики. Это –“тяготеющие”,”тяжёлые” или ”гравитационные” массы.

12.2Потенциальная энергия гравитационного взаимодействия, гравитационный потенциал.

Потенциальная энергия взаимодействия численно равна работе сил взаимодействия по перемещению взаимодействующего тела из данного положения в бесконечность:

∞

Fdx =

∞

−

γmM

dx =

γmM

∞

γmM

∫

= −

(220)

Энергетической характеристикой поля является гравитационный потенциал, равный потенциальной энергии единичной пробной массы, помещённой в данную точку поля:

V		=	Eгр	= −	γM
	гр				(221)

			m		r

12.1.Связь напряжённости и потенциала поля.

На расстояниях r1 и r2 от источника поля напряжённости поля равны:

− γM	и − γM
r2	r2
1	2

Вэтих же точках определим потенциалы:

−γM и − γM

Изменение потенциала на единицу длинны:

γM (r

− r )

Vгр

γM

−

r1r2 r

r1r2

Если точки расположены бесконечно близко друг к другу, связь напряжённости и потенциала принимает вид:

Eгр = −	dVгр	(222)
	dr

12.2. Зависимость веса тела от высоты.

Для небольших высот (малы по сравнению с радиусом Земли) вес тела:

−

γmM

= P

− 2

(223)

(R + h)2

+ 2

Где P0 - вес тела на поверхности Земли.

Гравитационное взаимодействие между телами конечных размеров. 12.5.1.Взаимодействие между материальной точкой и тонким кольцом.

Материальная точка массы	m находится на расстоянии r от тонкого кольца массы
M (рис.52). Выделим два	элемента кольца массы	dM , расположенные на концах
расположенные под углом	da из его центра. По	закону всемирного тяготения сила

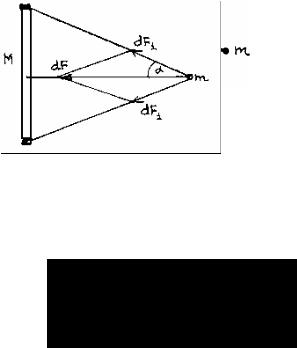
взаимодействия dF1 между точкой и каждым из элементов равна:

dF	= − γmdM	= − γmMdα	(224)
1	r2	2πr2
	r2	2πr2
	1	1

Равнодействующая сила взаимодействия с двумя выделенными элементами направлена к

центру кольца и равна: dF = 2dF	r	= −	γmMdα r	(225)

1 r			πr
	1		1

Полную силу взаимодействия можно получить, интегрируя (225):

π	γmMπ		γmM
F = ∫dF = −	γmMπ	r = −	γmM	r	(226)
F = ∫dF = −	πr3	r = −	r3	r	(226)
0	1		1

Рис.52

12.5.2. Взаимодействие точки с тонким сферическим слоем.

Пусть точечная пробная масса m находится на расстоянии r от центра слоя радиуса R и массы M (рис.53).

Рис.53 Выделим в слое тонкое кольцо, радиус которого виден из центра слоя под углом ϕ , а

поперечный размер (ширина кольца) – под углом dϕ . По (226) сила взаимодействия между точкой и выделенным кольцом равна:

	dF = − γmM (r		− R cosϕ)				(227)
		r3
		1
где:
dM =	M 2πR2	sinϕdϕ	=		1	M sinϕdϕ
dM =	4πR2		=	2		M sinϕdϕ
	4πR2			2
масса кольца.
Таким образом:	dF = − γm(r − Rcosϕ)M sinϕdϕ
	dF = − γm(r − Rcosϕ)M sinϕdϕ						(228)
				2r3
				1

Перейдем в 226 к одной переменной:

r12 = r2 + R2 − 2rRcosϕ r1dr1 = rRsinϕdϕ

откуда:

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.03.2016803.88 Кб12Lektsii_DU_prof_Gromak__chast_2.pdf
#
03.09.2019105.98 Кб16Lektsii_IGiPZS.docx
#
23.11.2019483.84 Кб80Lektsii_IGPB.doc
#
29.02.2016383.97 Кб159Lektsii_Laguna.docx
#
01.03.201623.1 Mб12Lektsii_Levakova_po_matanalizu.pdf
#
29.02.20161.41 Mб6Lektsii_Mekhanika_Ch_1.pdf
#
29.02.2016728.03 Кб5Lektsii_Mekhanika_Ch_2.pdf
#
29.02.20162.06 Mб6Lektsii_Mekhanika_Ch_3.pdf
#
16.04.20191.14 Mб1Lektsii_Nalogi_i_nalogooblozhenie-_2011.doc
#
22.11.201992.2 Кб2LEKTsII_Nemetskaya_klassicheskaya_filosofia_Fil...docx
#
15.08.2019113.83 Кб8Lektsii_Osnovy_ekologii_i_energosberezheni.docx