Лекции Дет. модели. Часть 1

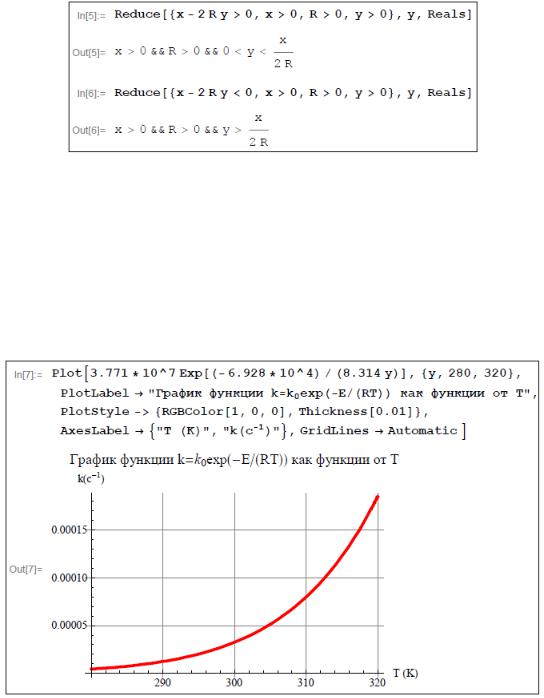
Единственная точка графика, в которой вторая производная функции об-

ращается в нуль, это точка x/(2R);k/e2 . Следующие математические выкладки доказывают, что она является точкой перегиба графика функции.

Итак, график функции является вогнутым на промежутке 0;x/ 2R и выпуклым на промежутке x/ 2R ; , единственная точка перегиба графика функции – это точка x/ 2R ;k /e2 .

Полное исследование функции z y в общем виде завершено. Построим график этой функции при конкретных значениях числовых пара-

метров: k k0 3,771 107 c 1; x E 6,928 104 Дж/моль. Приведем два графика, соответствующие различным диапазонам изменения пере-

менной y T : от 280 до 320 K и от 0 до 10000 K.

31

Упражнение. При помощи команды Plot изобразите график функ-

E

ции k k0e RT , считая, что это функция двух переменных E и T . Дано,

что k0 3,771 107 c 1, R 8,314 Дж/ K моль , промежутки изменения

4. Анализ полученных результатов. В неизотермической ки-

нетике для многих элементарных реакций уравнение Аррениуса

E

k k0e RT является приемлемой математической моделью, описывающей зависимость константы скорости реакции от абсолютной температуры и энергии активации.

а) Исследована функциональная зависимость между энергией активации и значением константы скорости элементарной реакции. Абсолютная температура в данном случае считалась фиксированной положительной величиной. Проведенное математическое исследование (если его рассматривать в соответствующем физико-химическому смыслу задачи диапазоне значений аргумента) адекватно представляет химический процесс, описываемый математической моделью. Результат k(0) k0 соответствует случаю, когда температура постоянна и энергия активации равна нулю. Этот случай рассматривают в изотермической кинетике.

32

Рис. 2.2.3

Исследование функции при помощи ее первой производной показывает, что при T 0 константа скорости реакции монотонно возрастает, оставаясь строго меньше значения k0 для всех рассматриваемых значений аргумента. С химической точки зрения первая производная функции является мерой чувствительности константы скорости реакции к влиянию абсолютной температуры, причем в данном случае первая производная положительна при T 0. Исследование функции при помощи ее второй производной показывает, что чувствительность константы скорости реакции k к влиянию абсолютной температуры T монотонно возрастает при 0 T Е/(2R) и монотонно убывает при Е/(2R) T . Таким образом, чувствительность константы скорости реакции k к влиянию абсолютной температуры T максимальна в точке перегиба графика функции E/ 2R ;k0 /e2 .

3. ХИМИЧЕСКИЕ РАВНОВЕСИЯ, ОПИСЫВАЕМЫЕ НЕЛИНЕЙНЫМИ УРАВНЕНИЯМИ

3.1.Определение рН водного раствора соли уксусной кислоты

1.Постановка задачи. Концентрация ацетата натрия в водном растворе составляет CCH3COONa 0,1M. При T 25°C определите pH

этого раствора (считайте, что искомое значение pH принадлежит отрезку 0;14 ). Проанализируйте полученный результат с химической точки зрения. Константу диссоциации уксусной кислоты примите равной

K 1,75 10 5. Используйте известную формулу для вычисления ионно-

го произведения воды: Kв H OH 10 14 (здесь и далее квадратные скобки используются для обозначения концентрации). При построении

34

математической модели рассматриваемого химического процесса считайте, что соль CH3COONa диссоциирует полностью, т. е. концентрация ионов натрия равна данной в условии концентрации CCH3COONa соли в растворе.

2. Математическая модель. Ацетат натрия CH3COONa пред-

ставляет собой соль уксусной кислоты CH3COOH – слабой одноосновной кислоты. Устанавливающиеся в водном растворе равновесные концентрации уксусной кислоты в ионизированном и неионизированном состоянии, а также концентрации протонов водорода и ионов гидроксила

Чтобы решить задачу, необходимо найти концентрацию H ионов водорода и определить pH водного раствора ацетата натрия, пользуясь известной формулой

Согласно условию, при построении математической модели рассматриваемого химического процесса считают, что соль CH3COONa диссоциирует полностью, т. е. концентрация ионов натрия равна данной в ус-

Теперь необходимо с помощью констант, данных в условии, выразить концентрации CH3COOH и OH через концентрацию H . Это позволит получить уравнение относительно одной неизвестной переменной

H , через которую и выражается по формуле (2.3.2) pH водного раствора.

35

Концентрации CH3COOH и OH выразим из формул (2.3.1):

ловии задачи константы:

CH3COO H CCH COONa OH H CCH COONa Kв .

3 3 H

Итак, уравнение (2.3.5) можно переписать так:

После умножения его левой и правой частей на ненулевое выражение

H K и проведения алгебраических преобразований оно примет вид

Это уравнение – кубическое с действительными коэффициентами. Следовательно, оно имеет три комплексных корня, из которых хотя бы один является вещественным. В условии сказано, что искомое значение pH принадлежит отрезку 0;14 . Следовательно, согласно формуле (2.3.2) интересующий нас в математическом смысле диапазон значений иско-

мой переменной – концентрации H ионов водорода – будет таким:

10 14;1 . Отметим, что ситуация, когда гидролиз отсутствует, соответст-

вует случаю H 10 7. Итак, математическая модель поставленной за-

дачи состоит из уравнения (2.3.6), где искомая переменная H принад-

лежит отрезку 10 14;1 , и формулы (2.3.2). Найдем интересующее нас приближенное решение уравнения (2.3.6) с недостатком и с избытком,

так чтобы по модулю разность этих значений была меньше 2 10 9 (при этом будем использовать методы приближенного решения конечных уравнений, а именно, метод хорд и метод касательных).

3. Решение математической модели средствами компью-

терной системы Mathematica. Прежде всего, приведем ряд встроенных функций компьютерной системы Mathematica, которые могут быть использованы при решении задач данного раздела.

36

Приведем фрагменты программного кода, снабженные пояснениями и комментариями. Перепишем для удобства уравнение (2.3.6) в виде

x3 k c x2 wx wk 0, обозначая искомую концентрацию H через x и предполагая соответствующие замены констант. Введем в рассмотрение функцию y x3 k c x2 wx wk, где x 10 14;1 . Зададим точные значения всех констант.

Изобразим график функции y x3 k c x2 wx wk на промежутке

[10-14;1].

38

Вычислим значение функции в точках x 10 14, x 0,2.

Функция y x3 k c x2 wx wk непрерывна на промежутке [10-14;1]. На концах рассматриваемого отрезка она принимает значения, разные по знаку. Следовательно, на нем существует хотя бы один вещественный корень уравнения x3 k c x2 wx wk 0. По виду графика мы можем лишь сказать, что все вещественные корни уравнения, принадлежащие отрезку [10-14;1], принадлежат отрезку [10-14;0,2]. Проведем исследо-

вание функции y x3 k c x2 wx wk, целью которого является отделение корней уравнения (2.3.6), т. е. построение таких отрезков (которые включает в себя отрезок [10-14;1]), на каждом из которых находится только один вещественный корень уравнения.

Сначала исследуем функцию при помощи ее первой производной.

Первая производная функции непрерывна на промежутке [10-14;1]. Следовательно, критические точки функции, принадлежащие рассматриваемому промежутку, отсутствуют. Получены точное и соответствующее

ему приближенное значения x 1000175 2250087507657 ; 30000000

39

x 4,99926 10 14 стационарной точки функции, принадлежащей отрезку [10-14;1]. Обозначим ее для краткости через st.

Убедимся в том, что стационарная точка является точкой экстремума данной функции.

Действительно, x=st является единственной точкой локального экстремума (минимума) рассматриваемой на отрезке [10-14;1] функции. Вычислим значение функции в этой точке.

40