
Лекции Дет. модели. Часть 2
.pdf4. ИНТЕГРАЛЫ ОТ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ. АНАЛИТИЧЕСКОЕ И ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
ВРЯДЕ ЗАДАЧ ХИМИЧЕСКОГО СОДЕРЖАНИЯ
4.1.Задача о концентрации раствора
1.Постановка задачи. Глубокий резервуар, объем которого равен Vр , изначально содержит a кг соли на 100 л ее водного раствора. В те-
чение каждой минуты в него поступает b литров воды и из него вытекает c литров раствора, причем b c. Началу процесса соответствует время t0 0. Определите, какое количество соли x1 (кг) останется в резервуаре через t1 минут после начала процесса, если предположить, что смесь мгновенно перемешивается.
2.Математическая модель. Введем следующее обозначение: x(t) – количество (кг) соли, содержащееся в резервуаре, в момент вре-
мени |
t (t t0). |
Из условия следует, что началу процесса соответствует |
||
время |
t0 0. |
Рассмотрим временной отрезок |
t;t t , |
где |
t 0; t 0, t 0. Согласно введенным обозначениям, |
x(t t) |
– это |
||
количество соли в резервуаре в момент времени t t, а x(t) – это количество соли в резервуаре в момент времени t. Тогда x(t) x(t t) xx 0 – это количество соли, которое убыло из резервуара за времяt 0. Объем раствора в резервуаре в момент времени t равен V t 100 (b c)t. Тогда концентрация соли (кг/л) в момент времени t
равна |
x(t) |
|
. Учитывая, что t 0, можно записать следующее |
||
|
|
||||
|
100 (b c)t |
|
|
||
равенство: |
|
|
x(t) |
|
|
|
|
x |
c t, t 0; t 0, t 0. |
||
|
|
|
|||
100 (b c)t
Перепишем это уравнение в дифференциальной форме:
|
x |
|
dx |
|
cdt . |
|
||
|
100 (b c)t |
|
Его можно записать как обыкновенное дифференциальное уравнение с разделенными переменными
dx |
|
cdt |
. |
|
100 (b c)t |
||
x |
|
||
|
|
48 |
|
Проинтегрируем это уравнение, расставив пределы интегрирования в определенных интегралах следующим образом:
x1dx |
t1 |
dt |
||
|
|
c |
|
. |
x |
|
|||
a |
0 |
100 (b c)t |
||
|
|
|
||
Остается найти определенные интегралы и выразить необходимое количество соли x1 через время t1 и заданные в условии постоянные.
3. Решение математической модели средствами компью-
терной системы Mathematica. Прежде всего, приведем ряд встроенных функций компьютерной системы Mathematica, которые могут быть использованы при решении задач данного раздела.
Обозначение встроенной функции |
Действия |
Clear[a] |
Удаляет числовое значение или определение, присво- |
(a=.) |
енное переменной a, которая представляет собой |
|
символ или строку. Значение, присвоенное перемен- |
|
ной, сохраняется в течение всего сеанса работы с сис- |
|
темой Mathematica, поэтому часто возникает необхо- |
|
димость «очистить» переменную с помощью указан- |
|
ной команды. Приступая к решению новой задачи в |
|
рамках одного сеанса работы с системой Mathematica, |
|
полезно «очистить» все введенные ранее переменные |
|
(символы и строки) с помощью команды |
|
Clear["Global`*"]. Заметим, что переменная, в |
|
записи которой имеются нижние или верхние индек- |
|
сы (например, a0), не воспринимается системой |
|
Mathematica как символ или строка. Чтобы «очи- |
|
стить» такую переменную, используют команду |
|
Unset[a0](кратко это записывают так: a0=.). Эту |
|
же команду можно использовать, чтобы «очистить» |
|
переменную a, которая представляет собой символ |
|
или строку. |
D[f[x],{x,n}] |
Вычисляет n-ную производную функции f[x] по |
|
переменной x. В случае n=1вместо {x,n} пишут x. |
Integrate[f[x],x] |
Вычисляет неопределенный интеграл от функции |
|
f[x] по переменной x. Произвольную константу, ко- |
|
торая возникает при интегрировании, полагают рав- |
|
ной нулю. Система Mathematica вычисляет большин- |
|
ство интегралов, которые выражаются через стан- |
|
дартные математические функции, а также позволяет |
|
интегрировать выражения, содержащие специальные |
|
функции. Если система не может представить резуль- |
|
тат интегрирования в виде формулы, то она выдает |
|
введенное выражение без изменений. |
|
|
|
49 |
Обозначение встроенной функции |
|
Действия |
|
|
Integrate[f[x], |
Вычисляет определенный интеграл от функции f[x] |
|||
{x,xmin,xmax}] |
по переменной x в пределах интегрирования от xmin |
|||
|
до xmax. Если результат интегрирования не может |
|||
|
быть представлен в виде формулы, то введенное вы- |
|||
|
ражение система выдает без изменений. |
|
||
N[x,n] |
Преобразует точный результат x в приближенный c |
|||
|
заданной точностью n значащих цифр. |
|
||
NIntegrate[f[x], |
В случае, когда определенный интеграл не содержит |
|||
{x,xmin,xmax}] |
неизвестных числовых параметров, дает численный |
|||
|
результат интегрирования функции f[x] по пере- |
|||
|
менной x в пределах интегрирования от xmin |
до xmax. |
||
Plot[{f1[x],f2[x],…, |
Строит на |
одном рисунке |
графики |
функций |
fn[x]},{xmin,xmax}] |
f1[x],f2[x],…,fn[x] одной переменной x на от- |
|||
|
резке [xmin,xmax]. Существуют команды (формат их |
|||
|
различен в различных версиях), например, |
|||
|
Needs["PlotLegends`"] ‒ в версии Mathematica |
|||
|
7.0, <<Graphics`Legend` ‒ в версии Mathematica |
|||
|
5.2, которые подключают средства системы |
|||
|
Mathematica, |
дающие возможность подписать графи- |
||
|
ки на полученном рисунке. |
|
|
|
ReplaceAll |
Оператор подстановки, который применяет список |
|||
(expr/.rules) |
правил замены rules к выражению expr. |
|
||
Simplify[expr] |
Находит для выражения expr |
простейшую форму, |
||
|
применяя к нему стандартные алгебраические преоб- |
|||
FullSimplify[expr] |
разования. |
|
|
|
Находит для выражения expr |
простейшую форму, |
|||
|
применяя к нему более широкий спектр преобразова- |
|||
|
ний. |
|
|
|
Solve[eqns,vars] |
Делает попытку решить в символьной форме систему |
|||
|
уравнений eqns относительно |
переменных vars |
||
|
(более подробное описание действия команды можно |
|||
|
посмотреть в предыдущих разделах). |
|
||
Приведем фрагменты программного кода, снабженные пояснениями и комментариями. Сначала по формуле Ньютона ‒ Лейбница найдем опре-
x1dx |
t1 |
dt |
||
деленный интеграл из левой части равенства |
|
c |
|
. |
x |
|
|||
a |
0 |
100 (b c)t |
||
|
|
|
||
50

Затем найдем определенный интеграл из правой части этого равенства и умножим его на число (–с).
Выразим искомую переменную x1 через время t1 и заданные в условии постоянные.
С целью построения графиков зададим конкретные числовые значения параметров а, b и c и укажем формулы соответствующих функциональных зависимостей между количеством соли x1 и временем t1. Для наглядности построим графики этих функциональных зависимостей.
51
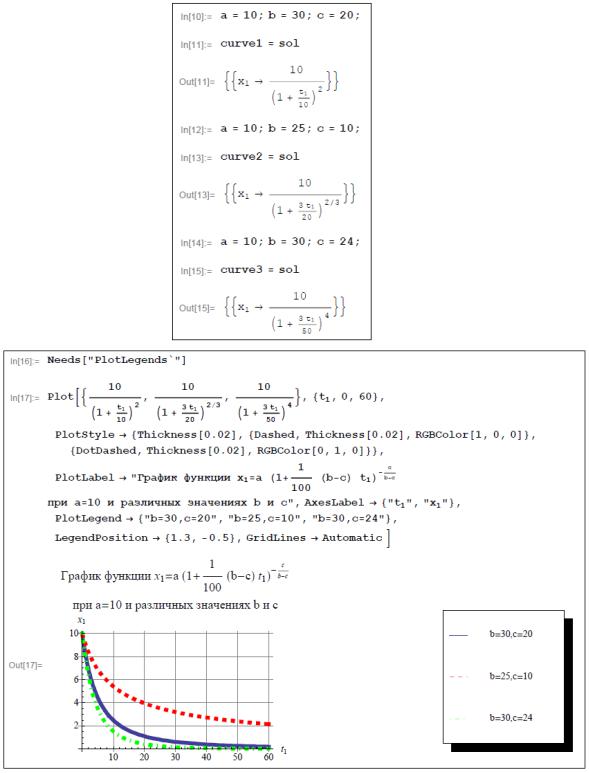
4. Анализ полученных результатов. Формулы в решении ма-
тематической модели записаны с тем расчетом, что b c 0. Это соответствует условию задачи, где сказано, что b c. Следует отметить, что математическая модель задачи адекватно отражает описываемый с ее
52
помощью процесс в том случае, если объем раствора V 100 (b c)t в резервуаре меньше или равен объему резервуара Vр . Итак, полученная
средствами системы Mathematica символьная форма решения поставленной задачи корректна с математической точки зрения и адекватна хими-
ческому содержанию задачи при t |
0; |
Vр 100 |
|
. В компьютерном виде |
|
|
|||
1 |
|
b c |
|
|
|
|
|
|
получены зависимости между переменными t1 и x1 при конкретных значениях числовых параметров a,b,c и приведен пример графического оформления этих результатов.
Замечание. Зная количество соли, оставшейся в резервуаре (его легко установить, измеряя объем, занимаемый раствором, и концентрацию соли в нем), можно определить, сколько времени прошло от начала процесса. Интересно, что в прикладных исследованиях аналогичные идеи используются для вычисления возраста морей и океанов.
4.2.Кинетика простых реакций
1.Постановка задачи. Рассмотрите прямую кинетическую задачу для случаев протекания простых реакций в закрытой изотермической системе (объем и температура постоянны) в предположении, что имеет место соответствие между кинетическим и стехиометрическим уравнениями реакции. Получите аналитическое решение прямой кинетической задачи, т.е. уравнения кинетических кривых. Представьте полученное решение графически. Проанализируйте результаты с химической точки зрения. Рассмотрите следующие случаи.
1.Схема простой реакции с единственным реагентом, идущая в одну
k |
n 1,2,3. Здесь CA |
|
0 – это |
стадию, такова: nA Продукты, |
0 |
||
|
|
|
начальная концентрация реагента A.
2. Схема простой реакции с двумя реагентами, идущая в одну ста-
k
дию, такова: A B Продукты. Здесь CA0 CB0 0 – это на-
чальные концентрации реагентов A и B соответственно.
3. Схема простой реакции с двумя реагентами, идущая в одну ста-
k
дию, такова: A B Продукты. Здесь CA0 0;CB0 0 – это
начальные концентрации реагентов A и B соответственно, причем
CA0 CB0.
53

2. Математическая модель. Прежде чем составлять математические модели, рекомендуется прочитать общие сведения из химической кинетики, изложенные в подразделе 1.3.
1. Число n – это порядок реакции, в данном случае совпадающий по величине со стехиометрическим коэффициентом. В зависимости от величины n выделим случаи моно-, би- и тримолекулярных реакций с участием одного реагента. В соответствии с принципами химической кинетики математические модели таких реакций представляют дифференци-
альными уравнениями |
dCA(t) |
nk CA(t) n, где |
n 1,2,3 соответствен- |
|
|||
|
dt |
|
|
но, с начальными условиями, отвечающими концентрациям реагента A в |
|||
момент начала реакции t 0. В каждом из рассматриваемых случаев (n 1,2,3) начальное условие имеет вид CA 0 CA0, где CA0 0. Ана-
литическое решение прямой кинетической задачи состоит в установлении функциональной связи между текущей концентрацией реагента и временем t(t 0), т. е. в получении уравнения кинетической кривой.
Дифференциальное уравнение dCA(t) nk CA(t) n можно записать как dt
уравнение с разделенными переменными dCA nkdt. Проинтегрируем
CAn
его, расставив пределы интегрирования в определенных интегралах следующим образом:
C |
A |
du |
t |
|
|
nk dt. |
|||
|
|
|
||
u |
n |
|||
CA |
|
0 |
||
|
0 |
|
|
|
Выражая с помощью системы |
Mathematica текущую концентрацию |
|||
CA t через время и заданные в условии константы, получим кинетическую кривую для каждого из случаев n 1,2,3.
2. В соответствии со стехиометрией реакционной схемы к моменту времени t 0 в единице объема реагируют одинаковые количества (моль) обоих реагентов, каждое из которых обозначим через x(t). Тогда текущие концентрации реагентов к этому моменту времени будут равны
CA t CA |
0 |
x(t),CB t CB |
0 |
x(t). Из |
условия равенства начальных |
|
|
|
CA t CB t . Поскольку имеет |
||
ненулевых концентраций следует, что |
|||||
место соответствие между кинетическим и стехиометрическим уравнениями, математическая модель реакции представляет собой обыкновен-
54

ное дифференциальное |
уравнение |
|
dCA(t) |
|
kCA(t)CB(t) kCA(t) |
2 |
с |
||||
|
|
dt |
|
||||||||
|
|
CA 0 CA |
|
|
CA |
|
0, и равенством |
||||
начальным |
условием |
0 |
, где |
0 |
|||||||
CA t CB t |
|
|
|
|
|
|
|
|
|||
(t 0). Следовательно, дифференциальная модель для это- |
|||||||||||
го случая аналогична дифференциальной модели из пункта 1, где n 2. 3. Согласно стехиометрии реакционной схемы к моменту времени t 0 в единице объема реагируют одинаковые количества (моль) обоих
реагентов, каждое из которых обозначим через x(t). Тогда текущие кон-
центрации |
|
реагентов к |
этому |
моменту времени будут равны |
|
CA t CA |
0 |
x(t),CB t CB |
0 |
x(t). |
В соответствии с принципами хи- |
|
|
|
|
||
мической кинетики и с условием задачи запишем дифференциальное
|
|
|
|
|
|
dC |
A |
(t) |
|
|
|
|
|
|
|
dC |
B |
(t) |
|
|
|
||
уравнение |
|
|
|
|
|
kCA(t)CB(t) |
|
|
|
|
|
|
kCA(t)CB(t) |
или |
|||||||||
|
|
|
dt |
|
|
|
|
dt |
|
||||||||||||||
|
dx(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
k C |
A |
0 |
x(t) C |
B |
0 |
x(t) с начальным условием x 0 0. Итак, ма- |
||||||||||||||||
|
|
||||||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
тематическая модель для случая 3 такова: |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
CA t CA x(t) |
(t 0), |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
CB t CB0 x(t) |
|
|
|
|
|
|
||||||
где CA0 CB0 – это заданные в условии ненулевые начальные концен- |
|||||||||||||||||||||||
трации реагентов, |
|
|
а x(t) |
– |
это |
|
решение |
задачи |
Коши |
||||||||||||||
|
dx(t) |
k C |
A |
0 |
x(t) C |
B |
0 |
x(t) , |
x 0 0, которую можно переписать в |
||||||||||||||
|
|
||||||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
t |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
|
|
|
|
||
интегральной форме: |
|
|
|
|
k dt. |
|
|
|
|||||||||||||||
CA0 u CB0 u |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|||||
3. Решение математической модели средствами компью-
терной системы Mathematica. Приведем фрагменты программного кода, снабженные пояснениями и комментариями.
C |
A |
du |
t |
|
|
nk dt, отдельно |
|||
1. Осуществляя интегрирование в формуле |
|
|
||
u |
n |
|||
CA |
|
0 |
||
|
0 |
|
|
|
рассмотрим случаи, когда n 1 и когда n 2,3, поскольку формулы интегрирования будут различными. Результат интегрирования выражения
1
un
система Mathematica выдает в предположении, что n 1.
55

Пусть n 1. С помощью формулы Ньютона ‒ Лейбница найдем интеграл, стоящий в левой части указанного равенства, и, учитывая, что интеграл из правой части равен t, выразим текущую концентрацию CA t через время и заданные в условии константы.
Таким образом, получено уравнение кинетической кривой для случая n 1: CA t CA0e kt (этот результат обозначен в программе sol1).
Пусть n 2. Проведем математические выкладки, аналогичные тем, которые были выполнены в предыдущем случае.
Получено уравнение кинетической кривой для случая n 2: CA t CA0 / 1 2ktCA0 (этот результат обозначен в программе sol2).
56
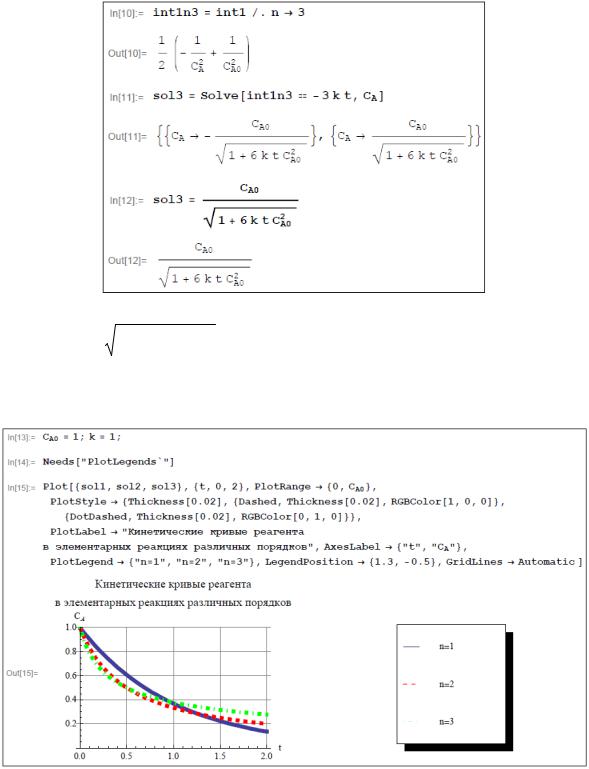
Пусть n 3. Производя действия, подобные уже рассмотренным в предыдущих двух случаях, получим два выражения для CA t , одно из которых не соответствует химическому смыслу задачи, поскольку является отрицательным для всех значений t 0.
Итак, получено уравнение кинетической кривой для случая n 3:
CA t CA |
0 |
/ |
1 6kt CA |
0 |
2 |
(этот результат обозначен в программе |
|
|
|
|
|
sol3).
Представим графически каждое аналитическое решение прямой кинетической задачи, полученное при рассмотрении случая 1.
57
