Лекции Дет. модели. Часть 2

Аналитическое выражение неопределенного интеграла слишком громоздко, и дальнейшая работа с ним затруднительна. Аналогичные проблемы возникают, если попытаться решить ту же самую задачу Коши при помощи встроенной функции DSolve системы Mathematica. Поэтому преобразуем подынтегральную функцию, раскрыв все скобки в ее знаменателе и введя некоторые новые обозначения.

Проинтегрируем ту же самую функцию с учетом новых обозначений.

Найдем теперь определенный интеграл, применяя формулу Ньютона – Лейбница, и получим в общем аналитическом виде решение задачи Коши из рассматриваемой математической модели. Заметим, что если по-

няя встроенную функцию DSolve системы Mathematica, то получим достаточно громоздкие выражения, причем компьютерная система ука-

78

жет на то обстоятельство, что некоторые решения задачи Коши, возможно, не найдены.

Итак, найдено в общем аналитическом виде решение задачи Коши из рассматриваемой математической модели, которое обозначено sol4.

Зададим определенные числовые значения констант скоростей прямой и обратной стадий и начальных концентраций всех веществ, участвующих в химической реакции. Подставим эти значения в sol4. Найдем для сравнения численное решение sol5 рассматриваемой задачи Коши в виде интерполяционной функции, предполагая, что t 0;60 . С этой целью воспользуемся встроенной функцией NDSolve.

79

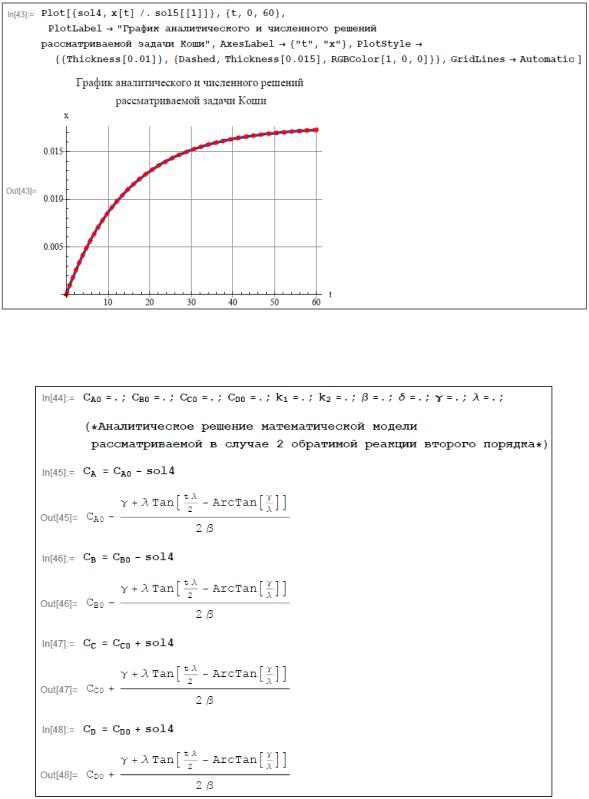
Убедимся в идентичности графиков численного решения и решения, полученного аналитическим путем.

Вернемся к аналитическому решению рассматриваемой задачи Коши и запишем в общем виде аналитическое решение математической модели обратимой реакции второго порядка.

80

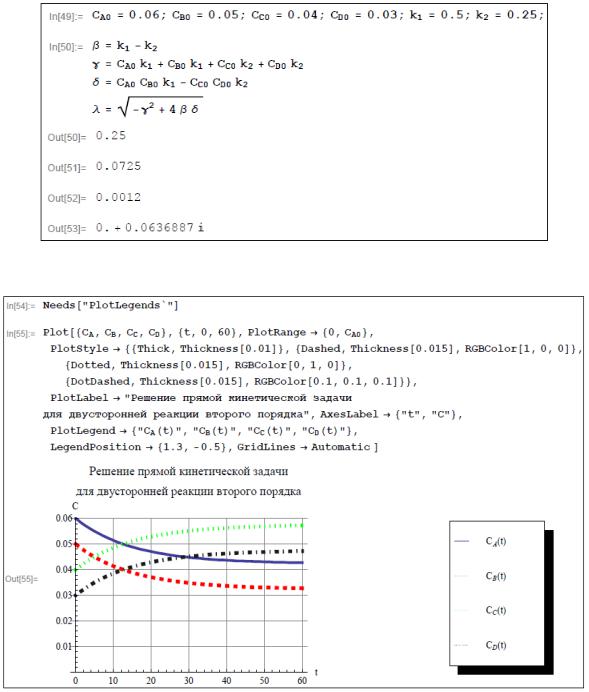
С целью построения графиков кинетических кривых зададим определенные числовые значения констант скоростей прямой и обратной стадий и начальных концентраций всех реагирующих веществ.

Представим графически полученные результаты. Приведем графики кинетических кривых для всех участников реакции.

Приведем также графики скоростей прямой и обратной стадий при тех же числовых значениях констант. Как и в случае 1, скорости прямой и обратной стадий двусторонней реакции второго порядка со временем

81

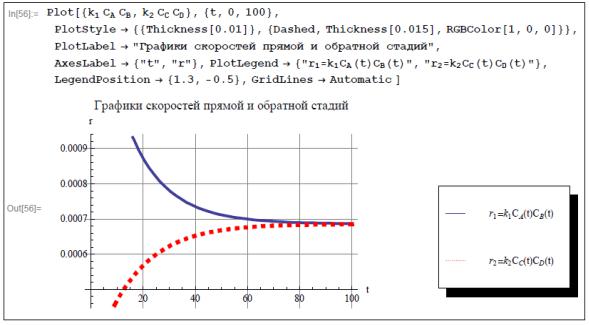
становятся практически одинаковыми, что соответствует состоянию динамического равновесия системы.

4. Анализ полученных результатов. В соответствии с принци-

пами химической кинетики получены аналитические решения прямых кинетических задач, сформулированных в пунктах 1, 2. Для каждой математической модели обратимой реакции приведены аналитическое решение соответствующей задачи Коши при помощи метода разделения переменных с последующим интегрированием и ее же аналитическое решение при помощи встроенной функции DSolve системы Mathematica. Дан сравнительный анализ полученных результатов. Кроме того продемонстрированы возможности численного решения системой Mathematica той же самой задачи Коши при определенных числовых значениях констант скоростей прямой и обратной стадий, начальных концентраций реагирующих веществ и в фиксированном временном интервале.

В случае 1 на основании проведенных математических исследований можно заключить, что текущая концентрация вещества А является монотонно убывающей, а текущая концентрация вещества В – монотонно возрастающей функциями при t 0. В химическом смысле скорость изменения как текущей концентрации реагента А, так и текущей концентрации реагента В, монотонно убывает при t 0. С течением времени концентрации обоих реагентов становятся практически не зависящими от времени, что соответствует состоянию равновесия. Равновесные кон-

82

k1 k2

CA0 CB0 k1 . Графики зависимостей скорости каждой из стадий реак- k1 k2

ции от времени иллюстрируют динамический характер химического равновесия: достижение равновесного состояния отнюдь не означает окончания процесса. При равновесии суммарная скорость реакции является практически нулевой за счет равенства скоростей прямой и обратной

стадий, имеющих значения, приближенно равные CA0 CB0 k1k2 . k1 k2

Аналитические выражения кинетических кривых в случае 2 включают в себя тригонометрическую функцию (тангенс) и обратную к ней. Наличие здесь такого типа функций выглядит, на первый взгляд, необычно. Дело в том, что компьютерная система Mathematica работает с комплекснозначными функциями и потому выдает результат в таком виде, хотя его же можно получить, используя натуральные логарифмы вещественнозначных аргументов. Тем не менее, полученные выражения вполне пригодны для проведения расчетов и построения графиков. Опуская детальный анализ всех кинетических кривых, заметим лишь, что основные выводы аналогичны выводам, сформулированным для случая 1. В качестве упражнения сформулируйте их самостоятельно.

С помощью полученных в пунктах 1, 2 аналитических выражений можно строить кинетические кривые для различных веществ, задаваясь конкретными числовыми значениями их начальных концентраций, а также значениями скоростей отдельных стадий двусторонней реакции.

Замечание 1. Термин «обратимые» реакции для описания типа химических превращений, рассмотренных в пункте 5.1.1, является не совсем удачным, поскольку с позиций термодинамики все без исключения реакции являются обратимыми. Здесь имеют в виду обратимость в формаль- но-кинетическом смысле, т. е. подразумевают, что константы скоростей обеих стадий имеют соизмеримые значения и нельзя пренебречь скоростью ни одной из элементарных стадий рассматриваемой сложной реакции.

CA0 x(t) k2 CB0 x(t) , полученное в случае 1 для двусторонней

реакции первого порядка записывают в иной форме. Раскрывая скобки в правой части этого дифференциального уравнения, получают:

83

вещества B, находящееся в единице реакционного объема к моменту установления равновесия, за вычетом начальной концентрации этого веще-

применяют для решения обратной кинетической задачи, но при этом обязательно нужна конкретная информация о состоянии равновесия.

Замечание 3. Вообще говоря, возможны восемь различных кинетических схем для двусторонних реакций второго порядка. Можно показать,

при рассмотрении случая 2, имеет место для любой из этих восьми схем, но в каждом случае параметры , , представляют собой различные комбинации констант скоростей и начальных концентраций реагентов.

5.1.2.Последовательные реакции

1.Постановка задачи. Рассмотрите прямую кинетическую задачу для случаев протекания последовательных реакций в закрытой изотермической системе (объем и температура постоянны) в предположении, что имеет место соответствие между кинетической и стехиометрической схемами реакции. Получите аналитическое решение прямой кинетической задачи, т. е. уравнения кинетических кривых. Представьте получен-

ное решение графически. Проанализируйте результаты с химической точки зрения. Предполагая, что k1 k2 k1 0,k2 0 , рассмотрите сле-

дующие случаи.

1. Схема последовательной реакции такова:

A k1 B k2 P.

Предполагается, что CA0 0,CB0 CP0 0 – это начальные кон-

центрации веществ A, B и P соответственно.

84

2. Схема последовательной реакции такова:

A k1 B k2 P.

Предполагается, что CA0 0,CB0 0,CP0 0 – это начальные

концентрации веществ A, B и P соответственно, причем все они попарно различны между собой.

3. Схема последовательной реакции такова:

A k1 B;B C k2 P.

Предполагается, что CA0 0,CC0 0,CB0 CP0 0 – это началь-

ные концентрации веществ A, C, B и P соответственно. 4. Схема последовательной реакции такова:

A k1 B;2B k2 P.

Предполагается, что CA0 0,CB0 CP0 0 – это начальные кон-

центрации веществ A, B и P соответственно.

2. Математическая модель.

1. Последовательными или консекутивными называют реакции, в ко-

торых продукты, образующиеся на предыдущих стадиях, являются реагентами для последующих стадий. Случай 1 представляет собой простейшую схему последовательной реакции, здесь образование конечного продукта P из реагента A идет через стадию образования промежуточного продукта B. Поскольку по условию имеет место соответствие между кинетической и стехиометрической схемами реакции, то каждая из стадий представляет собой реакцию первого порядка. Действуя согласно принципу независимости протекания реакций, составим систему обыкновенных дифференциальных уравнений

Математическая модель для случая 1 представляет собой данную систему с начальными условиями CA(0) CA0,CB(0) 0,CP(0) 0.

Дифференциальное уравнение, описывающее расходование во времени исходного реагента, полностью совпадает по форме с уравнением простой реакции первого порядка, рассмотренным в подразделе 4.2. Воспользуемся уже полученными там результатами и запишем уравне-

ние кинетической кривой для реагента A: CA(t) CA0e k1t . Подставим

дифференциальным уравнением первого порядка относительно неизвестной функции CB(t), которое может быть решено, например, методом Бернулли. Наконец, уравнение кинетической кривой для конечного про-

2. Случай 2 отличается от случая 1 только лишь значениями началь-

3. Даже при наличии двух элементарных стадий кинетические уравнения последовательной реакции значительно усложняются, если хотя бы одна из них протекает по закономерностям реакции второго порядка. В случае 3 образующийся на первой стадии промежуточный продукт B взаимодействует на второй стадии с реагентом C. Вторая стадия имеет второй порядок. Учитывая принцип независимости протекания реакций, составим систему обыкновенных дифференциальных уравнений

Математическая модель для случая 3 представляет собой указанную систему с начальными условиями CA(0) CA0,CB(0) CP(0) 0,

CC(0) CC0.

86

Зависимость концентрации реагента A от времени очевидна:

CA(t) CA0e k1t. Подставим эту формулу во второе дифференциальное

уравнение: dCB(t) k1CA0e k1t k2CB(t)CC(t). Уравнение кинетической dt

кривой для конечного продукта P получим из принципа материального баланса: CP(t) CC0 CC(t). Здесь мы исходим из того, что в соответст-

вии со схемой, молярное количество вещества C, прореагировавшее в единице объема реакционного пространства к моменту времени t 0, совпадает с молярным количеством вещества P, образовавшимся в единице указанного объема к этому моменту времени. Итак, математической моделью химического процесса, рассматриваемого в случае 3, является система уравнений

4. В четвертом случае первая стадия представляет собой реакцию первого порядка, а вторая стадия является реакцией второго порядка. Составим систему обыкновенных дифференциальных уравнений

Математическая модель для случая 4 представляет собой данную систему с начальными условиями CA(0) CA0,CB(0) CP(0) 0.

Зависимость концентрации реагента A от времени очевидна:

CA(t) CA0e k1t. Подставим эту формулу во второе дифференциальное

уравнение: dCB(t) k1CA0e k1t 2k2 CB(t) 2. Итак, математическая мо- dt

дель химического процесса, рассматриваемого в случае 4, такова: