I. Общие понятия

1.

Понятие о ДУ с ЧП...................................................................................................

2

2.

ДУ с ЧП первого порядка........................................................................................

4

3.

Квазилинейные ДУсЧП-1........................................................................................

6

4.

Системы ДУсЧП.......................................................................................................

7

5.

Замена независимых переменных в ДУ-2 с 2-мя незав. перем. ..........................

8

6.

Приведение к каноническому виду ДУ-2 с 2-мя незав. перем..........................

10

7.

Классификация ДУ-2с n независимыми переменными .....................................

12

8.

Приведение к канон.виду ДУ-2 с n незав.перем.................................................

13

9.

Исключение младший производных в ур-ниях 2-го порядка ...........................

14

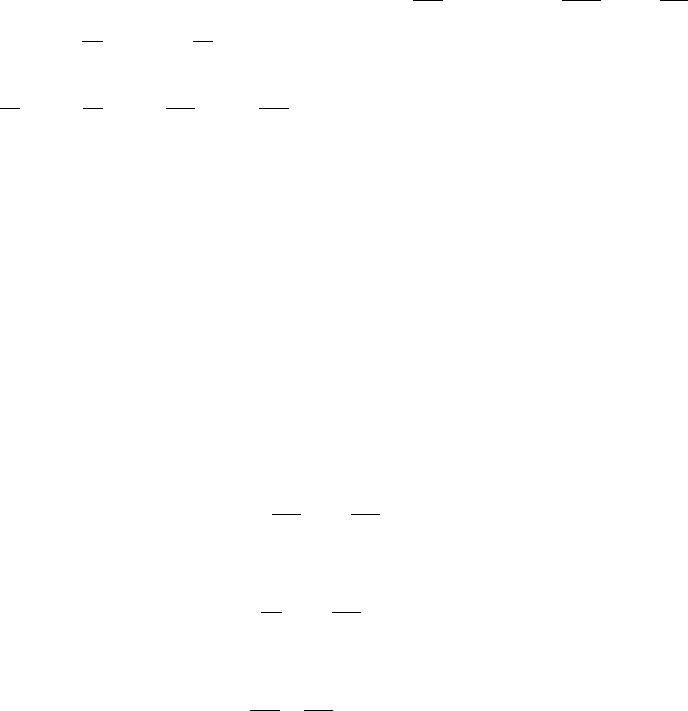
В случае 2 независ. переменных(4):

11

,

2

2

2

+

2 + 2 12 ,

+ 22 2

+ ,

+ ,

+ =,

( , )

→

2

( 1, 2)2

ставя в соответствие производн

координату:

Построим многочлен

→ 1,

→ 2 ;

2

→ 12,

2

→ 22 –характер. мн-лен для ур-ния (4).

1, 2

2

2

= 11 1 + 2 12 1 2 + 22 2

(1) – линейное однородное ДУсЧП-1

, ,

1

, … ,

= 0

(2), ф-ция u определена и

Рассмотрим лин. однор. ДУсЧП-1:

=1

= 0

непрерывна с 1-ми производными в

11

= =

(3). Ее можно

Ω

. Наряду с (2) рассм. сис-му ОДУ вида

n-1 обыкн. ДУ(4):

=

записать как систему из

1

1

.Установим соответствие между (2) и (4). Для этого полагаем, что

…

−1

−1

=

определены и непр. и имеют непр. производные 1-го порядка в некоторой

фикс. окр-ти

и они одновременно не обращаются в нуль в окрестности этой

( )

1

2

точки:

+ +

2

≠ 0

. Покажем, что

≠ 0

Ω(x 0

)

Теорема: Всякий интеграл системы (4) является решением ур-ния (2).

Док-во: (4) имеет

n-1

независимых интегралов. Пусть

=

- интеграл (4).

Тогда

, но

(5).

≡ 0

=

1 + +

1

1 =

1

Из (4) имеем (6):

…

−1

−1

1

−1

∙

+ +

∙

+

= 0

Подставим (6) в

(5):

=

или

−1

1

≡ 0

= 0

=

=1

.

=1

. Т.е.

– решение (2)/доказано

Обратная Теорема: Всякое решение (2) является интегралом системы (4)

≡ 0

Док-во: Пусть

– решение (2). Т.е.

=1

и выполн. (6).

1

1

(6)

−1

=

1

+ +

=

1

∙

+ +

−1

∙

+

=

и

≡ [

. . −

2 ] ≡ 0 = 0

=

=1

реш

/доказано

1

т к

– явл. интегр(4)

Теорема 3: Если

, … ,

−1

– ЛНИ системы (4), и

1

, … ,

−1

в обл.

, то F – решение

имеет непр.

0

производные

(2) – О.Р.(2).

-

F

−1

−1

Док во:

Подставим

Ω x в(2):

=1

=1

∙

=

=1

=1

=

вторая сумма

т к

[

≡ 0, .

.

−

решение

(2)] = 0

F

– решение (2) /доказано