ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ»
Кафедра «Высшая математика»
ВЫСШАЯ МАТЕМАТИКА
Методические указания к практическим занятиям для студентов всех специальностей дневной и заочной форм обучения
ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Могилев 2012
2
УДК 51
ББК 22.1 B 93
Рекомендовано к опубликованию учебно-методическим управлением
ГУ ВПО «Белорусско-Российский университет»
Одобрено кафедрой «Высшая математика» «10» февраля 2012 г., протокол № 6
Составители: ст. преподаватель А. М. Бутома; ст. преподаватель Т. И. Червякова
Рецензент канд. физ.-мат. наук, доц. С. Н. Батан
Методические указания содержат теоретические сведения по основным разделам математического анализа, образцы решения задач и упражнения для самостоятельной работы и под руководством преподавателя.
Учебное издание
ВЫСШАЯ МАТЕМАТИКА
Ответственный за выпуск |
Л. В. Плетнев |
||
Технический редактор |
А. А. Подошевко |
||
Компьютерная вёрстка |
Н. П. Полевничая |
||
Подписано в печать |
. Формат 60×84/16. Бумага офсетная. Гарнитура Таймс. |
||
Печать трафаретная. Усл.-печ. л. |
. Уч.-изд. л. |
. Тираж 99 экз. Заказ № 159. |
|
Издатель и полиграфическое исполнение Государственное учреждение высшего профессионального образования
«Белорусско-Российский университет» ЛИ № 02330/0548519 от 16.06.2009.
Пр. Мира, 43, 212000, Могилев.
© ГУ ВПО «Белорусско-Российский университет», 2012
3
1 Понятие функции. Основные элементарные функции
1.1 Теоретическая часть
Постоянной величиной называется величина, сохраняющая одно и то же значение.
Величина, сохраняющая постоянное значение в условиях данного процесса, называется параметром.
Переменной величиной называется величина, которая может принимать различные числовые значения. Если каждому значению x множества X x X поставлено в соответствие единственное значение y множе-
ства Y y Y , то переменная величина y называется функцией переменной x и обозначается y f x .
При этом x называется независимой переменной (или аргументом), y – зависимой переменной.
Множество X называется областью определения функции, множество Y – областью значений функции.
Способы задания функций:
а) аналитический способ, если функция задана формулой вида y f x ;
б) табличный способ, если функция задана таблицей, содержащей значения аргумента x и соответствующие значения функции y f x ;
в) графический способ, если функция изображена в виде графика; г) словесныйспособ, еслифункцияописанаправиломеёсоставления. К основным свойствам функции относятся чётность и нечетность,
монотонность, ограниченность, периодичность.
1.2 Образцы решения примеров
Пример 1 – Найти f 0 , |
f x , |
|
1 |
|
, если |
f x |
1 x |
2 |
. |
f |
|
|
|
||||||
|
|
x |
|
|
|
|
|
|
|
Решение
f 0 1 02 1 1;
f x 1 x 2 1 x2 ;
1 |
|
|
1 |
2 |
|
1 |
|
1 x2 |
1 x2 |
|
||||
f |
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
. |
x |
2 |
|
|
x |
|
|||||||||
|
|
|
||||||||||||
x |
|
|
x |
|
|
|
|
x2 |
|
|
|
|||
4
Пример 2 – Найти область определения функции y 4 6x x2 5 .
Решение
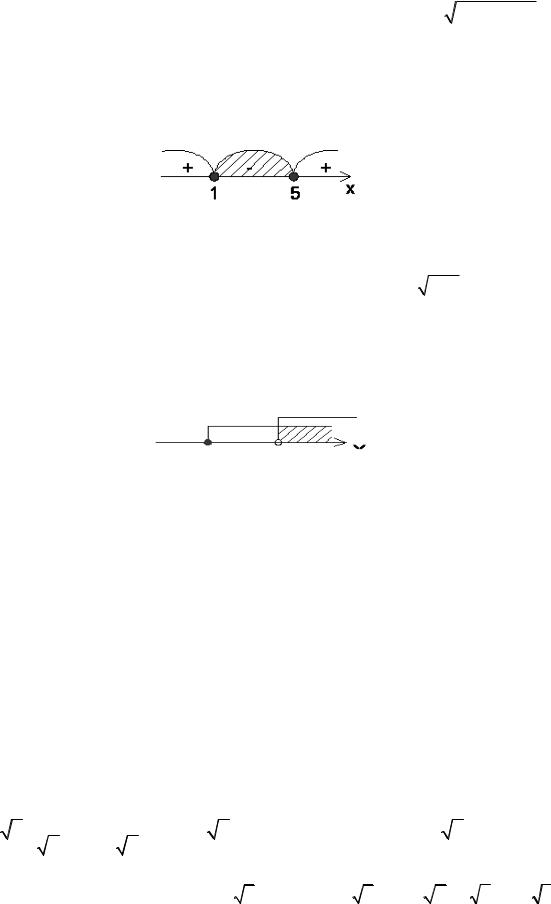
6x x2 5 0 ; x 1 x 5 0 .
Решаем неравенство методом интервалов.
Очевидно, что x 1; 5 . |
|
|
|
Пример3 – Найтиобластьопределенияфункции y |
x 1 lg 2x 3 . |
||
Решение |
|
x 1, |
|
x 1, |
|
|
|
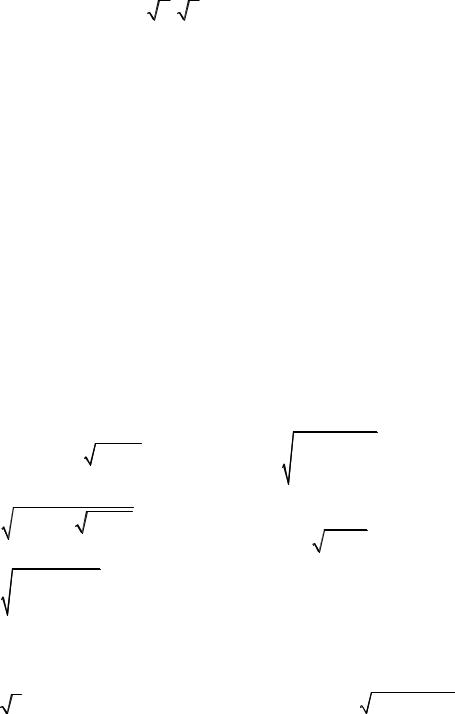
Имеем систему неравенств: |
0; |
|
|
2x 3 |
x 1,5. |
|
|
1 |
1,5 |
х |
|
|
|
|
|
|
|
|
|
||||
Область определения 1,5; . |
|
|
|
|
|
||
Пример 4 – Найти область определения функции y |
x |
||||||
|
. |
||||||
x2 3x 4 |
|||||||
Решение |
|
|
|
x 1, |
|||
x2 3x 4 0; |
x 1 x 4 0; |
||||||
|
|||||||
|
|
|
|
x 4. |
|||
Область определения функции X ; 1 1;4 4; .
Пример 5 – Найти область значений функции y sin x cos x .
Решение
Преобразуем функцию:
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
y |
2 |
|
|
sin x |
|
cos x |
|
2 |
sin |
4 |
sin x cos |
4 |
cos x |
|
2 sin x |
4 |
. |
|
2 |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таккак |
|
|
|
|
1, то |
|
2sin |
|
|
|
|
2 ; |
|
y |
|
|
2 ; |
2 y 2 . |
||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
sin x |
4 |
|
|
|
x |
4 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
5 |
|
|
Область значений y |
2; |
2 . |
|
|
|
|
|
|
|
|
|
Пример 6 – Выяснить четность (нечетность) функций: |
|||||
а) y x ctg3 x ; |
б) |
y x |
2x 1 |
; |
в) y x 1 2 sin2 x . |
|
|
|
2x 1 |
|
|
Решение: |
|
|
|
|
|
а) f x x ctg3 |
x x ctg3 |
x , т. к. f x f x , то функ- |
|||
ция нечетная; |
|
|
|
|
|
б) |
f x x 2 x 1 |
x |
2x 1 |
, т. к. |
f x |
|
2 x 1 |
|
2x 1 |
|
|
четная;
в) f x x 1 2 sin2 x x 1 2 sin2 x , т. к.
функция ни четная, ни нечетная.
f x , то функция
f x f x f x ,
1.3 Примеры для самостоятельной работы
1.3.1 Найти область определения функций:
а) |
y log3 sin x |
4 x |
2 |
; |
|
|
г) |
y |
3 x 2x2 |
|
|||||||
|
|
|
log2 |
x 1 |
; |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) y 2x 5 |
9 x2 ; |
|
|
|
д) y |
2x2 lg x 5 |
; |
||||||||||
|
|
|
8 x3 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) |
y |
log |
|
2x 1 ; |
|
|
|
|
е) |
y arccos |
2x |
|
. |
|
|
||
0,3 |
|
|
|
|
1 x2 |
|
|
|
|||||||||
|
|
|
x 5 |
|
|
|
|
|
|
|
|
|
|
|
|||
1.3.2 Найти область значений функций: |
|
|
|
|
|
|
|||||||||||
а) |
y |
3 sin x cos x ; |
|
б) y |
|
|
x |
; |
в) |
y |
x2 |
x 2 . |
|||||
|
1 |
x2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1.3.3 Определить четность (нечетность) функций:
а) |
y x |
3 |
sin x ; |
в) |
y lg |
1 |
x |
; |
д) y |
1 |
e |
x |
e |
x |
. |
|
1 |
x |
2 |
|
|
||||||||||
б) |
y x x3 5x5 ; |
г) |
y x2 |
sin x ; |
|
|
|
|
|
|
|
||||