
Podgotovka_k_sdache_modulya_5
.pdf
Учреждение образования «Белорусская государственная сельскохозяйственная академия»
Кафедра высшей математики
Методические указания
для подготовки к сдаче модуля №5 по теме «Неопределённый и определённый интегралы» и задания для самостоятельной работы студентов факультета бухгалтерского учёта
Горки, 2012
1
1. Неопределённый и определённый интегралы
1.1. Неопределённый интеграл и его свойства
Функция F(x) называется первообразной функцией для функции f(x), если F' (x) f (x) . Если F(x) есть первообразная функция для
функции f(x), то каждая из функций F(x)+C, где С – произвольная постоянная, будет также первообразной для функции f(x). Это означает, что если функция f(x) имеет хотя бы одну первообразную функцию, то она может иметь бесчисленное множество первообразных функций и все они отличаются друг от друга на постоянную величину.
Совокупность всех первообразных функций F(x)+C для функции f(x) называется неопределённым интегралом от функции f(x) и обо-
значается f (x)dx F(x) C . Процесс нахождения первообразной
функции называется интегрированием. Переменная х называется пе-
ременной интегрирования, функция f(x) называется подынтегральной функцией, выражение f(x)dx – подынтегральным выражением.
Неопределённый интеграл обладает свойствами, использование которых в значительной степени может упростить интегрирование функций:
Производная от неопределённого интеграла равна подынтегральной функции, т.е. f (x)dx ' f (x) .
Дифференциал неопределённого интеграла равен подынте-
гральному выражению, т.е. d f (x)dx f (x)dx.
Неопределённый интеграл от дифференциала функции равен этой функции плюс произвольная постоянная, т.е. dF(x) F(x) C .
Постоянный множитель можно выносить за знак интеграла:
kf(x)dx k f (x)dx.
Неопределённый интеграл от алгебраической суммы функций
равен |
алгебраической сумме |
интегралов от этих функций, т.е. |
f (x) g(x) dx f (x)dx g(x)dx . |
||
|
Результат интегрирования не зависит от обозначения перемен- |
|
ной интегрирования, т.е. если |
f (x)dx F(x) C , то при замене пе- |
|
|
|
2 |
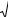
ременной интегрирования х на t |
f (t)dt F(t) C . Такое свойство |
|||||||||||||||||||||||||||
называется инвариантностью формулы интегрирования. |
||||||||||||||||||||||||||||
|
|
При интегрировании удобно пользоваться формулами, которые |
||||||||||||||||||||||||||
составляют таблицу основных интегралов: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
dx x C |
|
|
7 |
|
cos xdx sin x C |
|
||||||||||||||||||||
|
2 |
|
xndx |
|
x |
|
n 1 |
|
C |
8 |
|
|
|
|
|
1 |
|
|
|
|
tgx C |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
n 1 |
|
|
|
|
xdx |
|
|||||||||||||||
|
3 |
|
|
1 |
dx ln |
|
x |
|
C |
9 |
|
|
|
|
|
1 |
|
|
|
|
ctgx C |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xdx |
|
|||||||||||
|
4 |
|
exdx ex C |
10 |
|
|
|
|
|
1 |
|
|
dx arcsin x C |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|||||||
|
5 |
|
axdx |
a |
x |
C |
11 |
|
|
|
1 |
dx arctgx C |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||
|
|
lna |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
|
||||||||||
|
6 |
|
sin xdx cos x C |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Интегралы данной таблицы называются табличными. Каждая из формул таблицы справедлива в области определения подынтегральной функции.
1.2. Основные методы интегрирования
При интегрировании функций не всегда можно сразу использовать таблицу интегралов. Как правило, вначале нужно данный интеграл преобразовать таким образом, чтобы свести его к одной или нескольким формулам таблицы. Для этого используются специальные методы интегрирования, основными из которых являются непосред-
ственное интегрирование, замена переменной (или метод подстановки), метод интегрирования по частям.
Суть метода непосредственного интегрирования состоит в том, что данный интеграл с помощью алгебраических преобразований и
3

свойств неопределённого интеграла сводится к табличным интегралам. При этом часто удобно пользоваться некоторыми преобразованиями дифференциала, которые называются «подведением под знак дифференциала»:
du d(u a), где а – число;
du 1 d(au), где а – некоторое не равное нулю число; a
udu 1 d(u2 );
2
cosu du d(sinu) ;
sinu du d(cosu);
1 du d(lnu); u
|
1 |
|
|
|
du d(tgu) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
cos2 u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Примеры 1.1 – 1.4. Найти неопределённые интегралы: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
а) x6dx ; б) |
2x3 |
4x2 5 dx ; в) |
|
|
|
2 |
|
1 |
ex 4sin x |
1 |
|
|
|
|||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
dx; |
|||||||||||||||||||||||||||||||||||
|
|
cos |
2 |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
г) 34 x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
|
|
|
|
|
1 x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. а) |
x |
6 |
dx |
x6 1 |
C |
|
x7 |
C ; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
6 1 |
7 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
б) 2x3 4x2 5 dx =2 x3dx 4 x2dx 5 dx 2 |
x4 |
|
4 |
x3 |
|
|
||||||||||||||||||||||||||||||||||||
|
3 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
||||
|
1 |
|
x |
4 |
|
|
4 |
x |
3 |
5x C |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5 x C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
ex |
|
|
|
|
|
1 |
|
|
|
|
|
|
x2dx |
1 |
|
|
|
|
exdx |
||||||||||||||||
в) |
|
x2 |
|
|
|
|
|
4sin x |
|
|
|
|
|
|
dx |
= |
|
dx |
||||||||||||||||||||||||
|
|
|
|
|
|
cos |
2 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||
4

4 sin xdx |
1 |
|
dx |
x3 |
ln |
|
x |
|
ex |
4 ( cos x) tgx C |
|
|
|
||||||||
2 |
|
|
||||||||
|
cos |
x |
3 |
|
|
|
|
|
|
|
x3 ln x ex 4cos x tgx C ; 3
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
г) |
3 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx=3 x4 2 |
|
|
|
|
|
dx |
|
|
|
dx |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
1 x |
2 |
1 |
|
|
2 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
1 x |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
x4 |
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|||||||||||||||
3 x4 dx 2 x |
3 dx |
|
|
|
|
dx |
3 |
|
2 |
|
|
arctgx C |
||||||||||||||||||||||||||||||||||||||||||||||
|
1 x |
2 |
|
|
3 |
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
3 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
7 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
4 |
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
4 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
arctgx C |
|
|
x |
7 |
|
|
x |
2 |
|
arctgx C . |
|
|
|||||||||||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
7 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
4 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Если интеграл непосредственно не находится, то во многих случаях результат может быть достигнут с помощью метода замены переменной (подстановки). Данный метод помогает значительно упростить подынтегральное выражение и свести интеграл к одной из формул таблицы.
Если подынтегральная функция представляет собой дробь, у которой числитель есть производная знаменателя, то такой интеграл равен логарифму натуральному от абсолютной величины знаменателя,
|
|
f |
' (x) |
|
|
|
|
|
|
|
|
|
|
т.е. |
|
|
dx ln |
f (x) |
C . |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||||
|
|
f (x) |
|
|
|
|
|
|
|
|
|
||
|
Примеры 1.5 – 1.9. Найти интегралы: а) sin3xdx; |
||||||||||||
б) (3 x)5 dx ; в) 5 |
|
dx; |
г) xex2 dx; |
д) |
|
x2 1 |
dx . |
||||||
3x 4 |
|
||||||||||||
x |
3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3x 5 |
||
Решение. а) sin3xdx {заменим t=3x, тогда dt=3dx, dx dt} 3
5
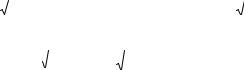
|
|
|
|
|
|
|
|
|
dt |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= sint |
|
|
|
|
|
|
|
|
|
|
|
sintdt |
|
|
( cost) C |
|
|
|
|
cos3x C |
; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
3 |
|
3 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
б) (3 x)5 dx ={заменим t=3 x, dt= dx, dx= dt}= t5 ( dt) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= t |
5 |
dt |
t6 |
|
|
C |
(3 x)6 |
C ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
6 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
в) 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
} 5 |
|
|
|
dt |
|
|
|
1 |
t |
1 |
dt = |
||||||||||||||||||||||||||||||
|
|
|
|
3x 4 |
dx={t=3x 4, dt=3dx, dx |
t |
|
|
|
|
5 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
3 |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
t |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 5 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
C |
|
|
|
|
|
t6 C |
|
5 (3x 4) |
6 C ; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) xex2 dx={t x2 , |
dt=2xdx, xdx |
dt |
|
}= et |
dt |
|
|
1 |
etdt |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
2 |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
t |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
|
e |
|
C |
|
|
|
e |
|
|
|
|
C ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
д) |
|
|
|
|
x2 1 |
|
|
|
|
dx ={t x3 3x 5, dt 3x2 3 dx 3 x2 1dx , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x2 1dx |
|
dt |
|
|
|
|
|
|
|
dt |
|
1 |
|
|
|
dt |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
t |
|
C |
|
x3 3x 5 |
|
C . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
} |
|
|
|
|
|
|
|
|
ln |
|
|
|
ln |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
t |
|
3 |
|
t |
|
3 |
|
|
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Если интеграл имеет вид udv, то для его нахождения использу-
ется формула интегрирования по частям udv uv vdu. Если в
результате получилось, что интеграл в правой части формулы проще, чем в левой, то применение этой формулы оправдано. Обычно в подынтегральном выражении за функцию u принимают тот множитель, который после его дифференцирования становится более простым. Оставшуюся часть подынтегрального выражения принимают за дифференциал dv некоторой функции v.
6
При использовании данного метода интегрирования удобно пользоваться следующими рекомендациями:
|
в интегралах вида P(x)ekxdx, |
P(x)sin xdx, |
P(x)cos xdx |
имеет смысл положить u=P(x), а в качестве dv взять оставшуюся часть подынтегрального выражения;
в интегралах вида |
P(x)arcsinxdx , |
P(x)arccos xdx , |
|
P(x)arctgxdx, |
P(x)arcctgxdx, |
P(x)ln xdx |
следует положить |
dv=P(x)dx, а оставшуюся часть подынтегрального выражения обозначить через u;
|
|
|
|
|
|
в интегралах вида |
eax sinbxdx, |
eax cosbxdx можно поло- |
|||||||||||||||||||||||||||||
жить u eax , |
а оставшуюся часть подынтегрального выражения при- |
||||||||||||||||||||||||||||||||||||
нять за dv. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Примеры 1.10 – 1.13. Найти интегралы: а) xcos xdx; |
|||||||||||||||||||||||||||||||||
б) |
(2x 1)e3xdx; |
в) |
ln xdx; г) x2e5xdx . |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
Решение. а) xcos xdx={u x, du dx, |
dv cos xdx, |
||||||||||||||||||||||||||||||||
dv cos xdx, |
|
v sin x}= xsin x sin xdx xsin x cos x C ; |
|||||||||||||||||||||||||||||||||||
|
|
|
|
б) (2x 1)e3xdx={u 2x 1, du 2dx, dv e3xdx, dv e3xdx, |
|||||||||||||||||||||||||||||||||
v |
1 |
e3x} (2x 1) |
1 |
e3x |
1 |
|
e 2dx |
1 |
(2x 1)e3x |
2 |
e3xdx |
||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
3 |
|
||||||||
1 |
|
|
|
|
|
|
3x |
|
2 1 |
|
|
3x |
|
1 |
|
|
3x |
2 |
|
3x |
|
|
|
||||||||||||||
= |
|
|
(2x |
1)e |
|
|
|
|
|
|
|
|
|
e |
|
|
C |
|
|
(2x 1)e |
|
|
|
|
e |
|
C |
||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
3 |
|
|
|
|
9 |
|
|
|
|
|
|||||||
1 |
|
e3x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
|
|
2x |
|
|
|
|
|
C |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
в) ln xdx={u ln x, du |
|
1 |
dx, dv dx, |
dv dx, v x}= |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
= xln x x |
1 |
dx xln x dx xln x x C ; |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) x2e5xdx ={u x2, |
du 2xdx, dv e5xdx, |
dv e5xdx, |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|

v |
1 |
e5x} |
x2 |
1 |
e5x |
1 |
e5x 2xdx |
1 |
|
x2e5x |
2 |
|
|
xe5xdx {к инте- |
|||||||||||||||||||||||||||||||||
|
5 |
|
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
5 |
|
|
|
|
|
|
||||||||||||
гралу ещё раз применим интегрирование по частям: u x, du dx, |
|||||||||||||||||||||||||||||||||||||||||||||||
dv e5xdx, dv e5xdx, v |
1 |
e5x} |
1 |
|
x2e5x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
1 |
|
|
|
|
|
1 1 |
|
|
|
||||||||||||||||
|
|
|
|
|
x |
|
e5x |
|
|
|
|
|
e |
5xdx |
= |
|
|
x2e5x |
|
|
|
|
|
|
|
xe |
5x |
|
|
|
|
|
e |
5x |
C |
||||||||||||
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
5 |
5 |
|
|
|
|
|
|
|
5 |
|
|
5 5 |
|
|
|
5 5 |
|
|
|
||||||||||||||||||||||||||
|
1 |
|
|
|
|
5x |
2 |
|
|
|
5x |
2 |
e5x C |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||
= |
|
|
|
x2e |
|
|
|
xe |
|
|
|
|
e |
5x x2 |
|
|
|
x |
|
|
|
C . |
|||||||||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
125 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
25 |
|
||||||||||||
1.3.Интегрирование рациональных и иррациональных функций
Функция вида R(x) P(x) называется рациональной дробью,
Q(x)
если её числитель и знаменатель являются многочленами. Рациональ-
ная дробь P(x) называется правильной, если степень числителя
Q(x)
меньше степени знаменателя. Если же степень числителя больше либо
равна степени знаменателя, то рациональная дробь P(x) называется
Q(x)
неправильной.
Всякая неправильная дробь может быть представлена в виде суммы многочлена и правильной дроби. Таким образом, интегрирование неправильной рациональной дроби сводится к интегрированию многочлена и правильной рациональной дроби.
Пример 1.14. Представить неправильную дробь |
2x2 |
3x 2 |
в |
|
|
x 2
виде суммы многочлена и правильной дроби.
Решение. Разделим числитель на знаменатель (деление много-
членов) и получим |
2x2 |
3x 2 |
=2x 1 |
4 |
. |
|
|
x 2 |
|
x 2 |
|
|
|
|
8 |
|
|
Дроби вида |
A |
, |
A |
, |
Ax B |
называются простейши- |
x a |
x a n |
x2 px q |
ми рациональными дробями. Всякую правильную дробь можно представить в виде суммы конечного числа простейших дробей.
Пример 1.15. Разложить правильную дробь |
2x 3 |
|
|
на про- |
|
|
||
|
(x 1)(x 3) |
|
стейшие.
Решение. Для разложения дроби на простейшие используем ме-
тод неопределённых коэффициентов: |
|
2x 3 |
= |
A |
|
B |
|
|
|||||
|
|
|
|
|
(x 1)(x 3) |
|
x 1 |
x |
3 |
|
|||
= |
A(x 3) B(x 1) |
|
Ax 3A Bx B |
|
(A B)x 3A B |
. |
Начальная |
||||||
|
(x 1)(x 3) |
|
(x 1)(x 3) |
|
(x 1)(x 3) |
|
|
|
|||||
дробь равна конечной и знаменатели у них одинаковы. Следовательно,
должны |
быть равными и |
числители: |
|
|
|
A B 2, |
Решая данную |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3A B 3. |
|
|
|||||||||||
систему уравнений, найдём: |
A |
5 |
, |
|
B |
3 |
. Тогда разложение дроби на |
|||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
A |
|
|
|
|
|
B |
|
|
||||||
простейшие имеет вид: |
|
2x 3 |
|
|
= |
5 |
|
|
|
|
|
|
|
3 |
|
. |
||||||||||||||||||||
|
(x 1)(x 3) |
|
|
x 1 |
|
|
x 3 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
||||||||||||||||||
При интегрировании простейших рациональных дробей можно |
||||||||||||||||||||||||||||||||||||
использовать формулы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
A |
dx A |
d(x a) |
dx A ln |
|
x a |
|
C ; |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
x a |
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(x a) n 1 |
|
|||||||||||
|
|
A |
|
dx A (x a) n d(x a) |
C = |
|||||||||||||||||||||||||||||||
(x a) |
n |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
||||||
|
= |
|
|
A |
C ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
(1 n)(x a)n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пример 1.16. Найти интеграл |
|
|
x3 2x2 |
3 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx. |
|
|
||||||||||||||||||
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x 3 |
|
|
|
||||||||||||||||||
Решение. Представим подынтегральную функцию в виде суммы многочлена и правильной дроби, предварительно разделив числитель
9
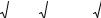
|
x3 |
2x2 3 |
x 4 |
11x 9 |
||
на знаменатель: |
|
|
|
|
. Разложим получен- |
|
|
x2 2x 3 |
|
x2 |
2x 3 |
||
ную правильную рациональную дробь на простейшие. Для этого вна-
чале знаменатель разложим на множители: |
x2 2x 3 0 , x |
3, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||
|
x2 |
1, |
x2 |
2x 3 (x 3)(x 1) . Тогда |
|
|
11x 9 |
|
|
|
|
11x 9 |
= |
||||||||||||||||||||||||||||||||||||||||||||
|
|
x2 2x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x 3)(x 1) |
|||||||||||||||||||
= |
|
A |
|
B |
|
|
A(x 1) B(x 3) |
|
Ax A Bx 3B |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
x 3 |
|
x 1 |
(x 3)(x 1) |
|
|
|
|
|
|
|
(x 3)(x 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
(A B)x A 3B |
. Так как |
|
|
11x 9 |
|
|
|
|
(A B)x A 3B |
, то |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
(x 3)(x 1) |
|
|
|
|
|
|
|
|
(x 3)(x 1) |
|
|
(x 3)(x 1) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
A B 11, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
1 |
|
, A |
21 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Решив данную систему, |
|
найдём |
|
|
|
|
|
|
. |
Тогда |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
A 3B 9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
||||||||||||||||||||
|
|
|
11x 9 |
|
|
11x 9 |
|
|
= |
|
|
21 |
|
|
|
|
|
1 |
|
|
|
. |
Подставим |
в подынте- |
|||||||||||||||||||||||||||||||||
|
x2 2x 3 |
(x 3)(x 1) |
2 x 3 |
2 x 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
2x |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
11x 9 |
|
|
|
|
|
|||||||||||||||||||
гральную функцию: |
|
|
|
|
dx= |
x 4 |
|
|
|
|
dx |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
2x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x 3)(x 1) |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
21 |
|
|
|
|
|
1 |
|
|
|
|
|
x2 |
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
= |
x 4 |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
4x |
|
|
|
ln |
x 3 |
|
|
|
ln |
x 1 |
C . |
||||||||||||||||||||||||||||||
|
|
|
|
|
2 x 3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
2 x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Если подынтегральная функция иррациональна, то с помощью замены переменной во многих случаях можно привести её к рациональному виду или к такой функции, интеграл от которой является табличным. Интегрирование при помощи замены переменной, которая приводит подынтегральное выражение к рациональному виду, называ-
ется интегрированием посредством рационализации подынтегрального выражения.
Интегралы вида |
|
n1 |
x |
m1 |
n2 |
x |
m2 |
ns |
x |
ms |
|
приводятся к |
R x, |
|
|
, |
|
,..., |
|
dx |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
интегралам от рациональных функций с помощью подстановки x tk , где k – наименьшее общее кратное чисел n1,n2 ,...,ns .
10
