
Podgotovka_k_sdache_modulya_5
.pdf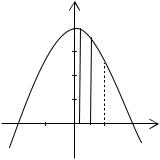
|
Найдём |
абсциссы |
|
точек |
пересечения |
линий: |
|
x2 x 6 x 2, |
|||||||||||||||
x2 4 0, x |
2, x |
2 |
2 . Тогда площадь заштрихованной фигуры |
||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
x |
3 |
|
|
2 |
|
|
равна |
x 2 |
x2 x 6 dx |
|
x2 |
4 dx |
|
|
|
4x |
|
|
||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
23 |
|
|
|
( 2)3 |
|
|
|
|
8 |
|
8 |
|
|
|
|
2 |
|
|
|
|||
|
|
4 2 |
|
|
4 ( 2) |
|
|
|
|
8 |
|
8 10 |
|
|
(кв. ед.). |
|
|||||||
|
3 |
|
|
3 |
|
|
|
|
3 |
|
3 |
|
|
|
|
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Пример 2.12. Вычислить объём тела, образованного вращением |
||||||||||||||||||||||
вокруг оси Ох плоской фигуры, ограниченной линиями |
y x2 |
4, |
|||||||||||||||||||||
y 0 , х=0, х=1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Решение. |
Изобразим в системе координат плоскую фигуру, |
ог- |
||||||||||||||||||||
раниченную заданными линиями.
у
4
•-2 |
0 |
|
|
|
|
• 2 х |
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
Полученная плоская фигура является криволинейной трапецией,
ограниченной сверху графиком функции y x2 4, а сбоку прямыми х=0 и х=1. Объём тела, образованного вращением этой трапеции
b
вокруг оси Ох, вычисляется по формуле Vx y2dx. В нашем случае
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
x5 |
|
|
|
x3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Vx x |
2 |
4dx x |
4 |
8x |
2 |
16 dx |
|
|
|
|
8 |
|
|
|
|
||||||||||
|
|
|
|
5 |
|
3 |
16x1 |
|
|||||||||||||||||
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||
|
15 |
|
13 |
|
|
|
0 |
5 |
|
|
03 |
|
|
|
|
|
8 |
|
|
|
|
|
|||
= |
|
8 |
|
|
|
16 1 |
|
|
|
|
8 |
|
16 0 |
|
13 |
|
|
|
(куб. ед). |
|
|
||||
|
5 |
|
|
3 |
|
|
|
|
5 |
|
|
3 |
|
|
|
|
|
15 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|

2.4. Задания для самостоятельной работы
1) Вычислить интегралы:
5 |
2t2 3t 2 dt ; б) |
||
а) |
|||
0 |
|
|
|
2 |
|
4x 3 |
|
д) |
|
dx; е) |
|
2x |
2 |
||
1 |
3x 4 |
||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
0 |
|
2 |
|
|||
|
3 |
|
xdx; в) cos xdx; г) |
sin2 xdx ; |
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
0 |
|
|
|
|
|
|
|
|
|
||
|
x |
|
1 x2 dx ; |
ж) xsin xdx ; |
||||||||
|
|
3 |
|
|
|
|
|
|
0 |
|
|
|
з) ln(x 1)dx ; и) x arctgxdx.
00
2)Вычислить площадь фигуры, ограниченной линиями:
а) y x2 2x 3, y 0 ; |
б) y x2 4x, y x 4 0; |
|
в) y x2 6x, y 0; г) |
y 2x2 ,x 1,x 2 ; |
|
д) |
y 3x2 6x,x 4, ось Ох на отрезке . |
|
3) |
Вычислить объём тела, образованного вращением вокруг оси |
|
Ох фигуры, ограниченной линиями y2 4x,x 2 . |
||
4) |
Вычислить объём тела, образованного вращением вокруг оси |
|
Оу фигуры, ограниченной линиями y x3,x 0, y 8 .
У ч е б н о – м е т о д и ч е с к о е и з д а н и е
Владимир Валерианович Куприянчик
Методические указания для подготовки к сдаче модуля №5 по теме «Неопределённый и определённый интегралы» и задания для самостоятельной работы
студентов факультета бухгалтерского учёта
22
