Методичка для практических занятий (2)

Таблица 3.1. - Производство яровой пшеницы в 24 хозяйствах:

Задание 3.2. Имеются данные за отчётный год по 30 малым предприятиям одной отрасли экономики, млн. руб.

Таблица 3.2. – Исходные данные

Продолжение таблицы 3.2.

С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском продукции произведите группировку предприятий по среднегодовой стоимости основных производственных фондов, образовав четыре группы предприятий с равными интервалами.

По каждой группе и совокупности предприятий в целом исчислите:

1)число предприятий;

2)среднегодовую стоимость основных производственных фондов – всего и в среднем на одно предприятие;

3)выпуск продукции – всего и в среднем на одно предприятие;

Дайте экономический анализ исчисленных показателей и сделайте выводы.

Задание 3.3. Провести перегруппировку нижеприведенных данных, образовав 4 группы. Результаты вторичной группировки изложить в таблице и дать краткие выводы.

Таблица 3.3. - Распределение работников двух СПК по уровню заработной платы за месяц:

Задание 3.4. Методом вторичной группировки по данным о распределении заводов по размеру основных производственных фондов (ОПФ) образовать группы заводов по следующему размеру основных производственных фондов, млн. руб.: 1 - 5; 5 - 10; 10 - 25; 25 - 50.

Таблица 3.4. – Распределение заводов по размеру основных производственных фондов

Задание 3.5. В результате ознакомления с материалами установлено, что в хозяйствах зоны имеются весьма существенные различия в качестве почв и количестве вносимых удобрений.

Таблица 3.5. - Имеются следующие данные по хозяйствам:

Продолжение таблицы 3.5.

Произвести комбинационную группировку хозяйств по качеству почв: разряд А - относительно худшие, Б - средние, В - лучшие почвы и по количеству вносимых удобрений подгруппы: до 4,0; 4,1 - 8,0; 8,1 и выше. Вычислить среднюю урожайность и валовой сбор по группам хозяйств. Полученные данные поместите в таблицу 3.6. и сделайте соответствующие выводы по группировке и таблицам.

Таблица 3.6. - Группировка хозяйств по качеству почв и количеству внесенных удобрений

8,1 и более

Итого

Всего

Задание 3.6. По данным статистических ежегодников и периодической печати подберите примеры статистических таблиц с перечисленными вариантами разработки сказуемого: а) с простой разработкой сказуемого; б) со сложной разработкой сказуемого по двум признакам.

Задание 3.7. Разработайте макеты: а) перечневой таблицы по территориальному принципу со сложной комбинированной разработкой сказуемого по двум признакам; б) перечневой таблицы по видовому принципу со сложной разработкой сказуемого в пространственно-временном разрезе; в) групповой таблицы со сложной комбинированной разработкой сказуемого в пространственном аспекте; г) групповой таблицы со сложной разработкой сказуемого в динамике; д) комбинационной таблицы с простой разработкой сказуемого в статике.

Задание 3.8. Разработайте макет статистической таблицы, характеризующей распределение численности занятого населения и безработных по семейному положению, и сформулируйте заголовок таблицы. Укажите: а) к какому виду таблицы относится макет; б) его подлежащее и сказуемое; в) признак группировки подлежащего.

Задание 3.9. Оформите в табличном виде следующие данные. Прожиточный минимум населения в РФ (в расчете на душу населения) возрос с 6369 (2011 г.) до 6510 руб./мес. (2012 г.). За этот же период прожиточный минимум возрос: трудоспособного населения с 6878 до 7049 руб./ мес.; пенсионеров с 5032 до 5123; детей с 6157 до 6259 руб./мес. Соотношение среднедушевого денежного дохода и прожиточного минимума всего населения увеличилось с 326,3 до 354,2 %. Сформулируйте название таблицы, укажите ее подлежащее и сказуемое и вид их разработки.

25

ТЕМА 4. ОБОБЩАЮЩИЕ СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ 4.1. Методические указания

Показатели, которыми статистика характеризует совокупности единиц в целом и по группам, называются обобщающими показателями; к ним относятся абсолютные, относительные и средние величины.

Первоначальным видом обобщающих показателей являются абсолютные величины. Их получают в результате статистического наблюдения, сводки или суммирования первичного статистического материала или расчетным путем.

Абсолютными величинами называются количественные сведения о всех сторонах как общественной жизни, так и явлений природы. В зависимости от размеров изучаемых явлений абсолютные величины бывают трех видов: индивидуальные, суммарные и расчетные. Абсолютные величины являются именованными числами и выражаются в натуральных, стоимостных и условных измерителях.

Относительные величины представляют собой отношение одних абсолютных показателей к другим, в этом заключается их экономический смысл. Относительная величина в статистике - это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных статистических величин.

Взависимости от целей исследования и исходной информации

относительные величины выражаются:

• в коэффициентах, если основание принимается за 1;

• в процентах (%), если основание принимается за 100;

• в промилле(0/00), если основание принимается за 1000;

• в продецимилле (0/000), если основание принимается за 10000.

Восновном все виды относительных величин, кроме интенсивности, выражаются в процентах. Для этого необходимо каждый относительный показатель умножить на 100.

По своему познавательному значению относительные показатели подразделяются на следующие виды: плана; выполнения плана, динамики, структуры, координации, сравнения и интенсивности.

Относительный показатель плана (ОПП) представляет собой отношение плановой величины ( yпл.) к величине, достигнутой в прошлом периоде ( y0 ):

ОПП упл ;

у0

Он показывает, во сколько раз намечаемый объем производства превышает достигнутый уровень, или сколько процентов от этого уровня составит.

Относительный показатель выполнения плана (ОПВП) – показатель, характеризующий уровень выполнения предприятием своих обязательств, предусмотренных в договорах;

26

Расчет производится путем соотношения фактически достигнутого объема в текущем периоде ( у1 )и объема обязательств по договору ( упл) .

Выражается в процентах или коэффициентах:

ОПВП у1

упл

Относительный показатель динамики (ОПД) – характеризует изменение изучаемого явления во времени, выявляет направление развития, измеряет интенсивность развития. Рассчитывается отношением величины текущего периода ( у1) к величине одного из прошлых периодов ( y0 ) :

ОПД у1 ;

у0

Рассчитанный показатель показывает, во сколько раз текущий уровень превышает предшествующий или какую долю от последнего составляет.

Произведение относительного показателя плана на относительный показатель выполнения плана дает относительный показатель динамики:

ОПД ОПП ОПВП;

Различают ОПД с постоянной и переменной базой сравнения. Если сравнение осуществляется с одной и той же базой сравнения, то получается ОПД с постоянной базой, при расчете с ОПД с переменной базой сравнения сравнение осуществляется с предшествующим уровнем.

ОПД с постоянной базой равен произведению ОПД с переменной базой, взятых в виде коэффициентов за весь анализируемый период.

Относительный показатель структуры (ОПС) – характеризует состав изучаемых совокупностей и исчисляется как отношение абсолютных величин каждого из элементов совокупности к абсолютной величине всей совокупности, т.е. отношение части ( уi ) к целому ( у) (удельный вес части

в целом). Выражается в процентах или долях:

ОПС уi ;

у

Относительный показатель координации (ОПК) – характеризует соотношение между отдельными частями статистической совокупности:

количественное соотношение одноименных показателей, относящихся к различным объектам статистического наблюдения, например, товарообороты различных предприятий:

например количество магазинов на 1000 человек и рассчитывается соотношением двух разноименных величин, связанных между собой:

Средней величиной в статистике называется общая характеристика совокупности по количественно изменяющемуся признаку, она показывает уровень признака, который относится ко всей совокупности. В зависимости от характера статистических данных применяют различные виды средних величин: средняя арифметическая, средняя гармоническая, средняя хронологическая, средняя геометрическая, средняя квадратическая и др.

Величина, для которой исчисляется средняя или, как говорят, осредняемый признак, обозначается х. Это может быть цена, заработная плата, урожайность, выполнение договорных обязательств, процент стандартной продукции и т.д. Отдельные значения или варианты величины х обозначаются через x1 , x2, x3,…, xn. Средняя величины х обозначается через " x ". Черта сверху символизирует процесс осреднения индивидуальных значений. Численность каждой варианты обозначают через f.

Среднюю арифметическую взвешенную можно определить как частное от деления суммы произведений вариантов на их численности (частоты)xf суммы численности (частот) f :

x ариф. взв. = xff ,

Когда веса (частоты) отсутствуют или равны между собой (f1=f2=...=fn),

применяется средняя арифметическая простая:

xариф.пр x

n

Средняя арифметическая является наиболее элементарной и в то же время всеобщей формой средней, но далеко не единственным видом средних величин.

Средняя гармоническая, представляет собой величину, обратную средней арифметической, исчисленную из обратных значений признака.

Среднюю гармоническую взвешенную можно определить как частное от деления суммы частот на отношение частот к вариантам:

Если частоты (веса) отсутствуют или равны между собой f1=f2=…=fn

применяется средняя гармоническая простая:

Средняя хронологическая используется для исчисления средних уровней моментного ряда динамики, когда показатели даны на определенную дату, на

28

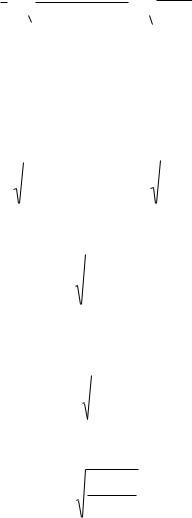
определенный момент времени. При исчислении средней хронологической число уровней моментного ряда больше фактического ряда на один уровень. Средняя хронологическая простая:

Средняя хронологическая взвешенная:

x x1 x2 f1 x2 x3 f2 ... xn xn 1 fn

2 fn

Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.

Средняя геометрическая исчисляется извлечением корня степени и из произведений отдельных значений – вариантов признака х:

x n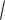x1 * x2 *...* xn n 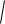xi

где n – число вариантов; П – знак произведения.

Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики.

Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:

где x1,x2,…xn – значения признака, n – количество вариантов признака.

Средняя квадратическая взвешенная:

где f – веса.

Средняя кубическая простая является кубическим корнем из частного от деления суммы кубов отдельных значений признака на их число:

где x1,x2,…xn – значения признака, n – их число.

Средняя кубическая взвешенная:

x 3 xi3 fi ,

fi

где f – веса.

4.2.Вопросы для самоконтроля

1.Какова роль статистических показателей в управлении экономикой и в чем состоят общие принципы их построения?

29

2.Понятие абсолютных показателей

3.Единицы измерения абсолютных показателей

4.Виды абсолютных показателей и способы их получения

5.Понятие и значение относительных показателей

6.Формы выражения и способы вычисления относительных показателей

7.Виды относительных показателей

8.Относительные показатели динамики

9.Относительные показатели плана, выполнения плана

10.Относительные показатели структуры

11.Относительные показатели интенсивности

12.Относительные показатели сравнения

13.Относительные показатели координации

14.Выбор базы при вычислении относительных показателей

15.В чем состоит роль и значение средних величин?

16.Как обосновать выбор вида степенной средней?

17.Как обосновать выбор весов при расчете взвешенной средней?

4.3.Тесты

1.Абсолютные величины могут выражаться: а) в натуральных единицах измерения б) в процентах

в) в условно-натуральных единицах измерения г) в денежных единицах измерения д) в виде простого кратного отношения е) в трудовых единицах измерения

2.Относительные статистические величины могут выражаться: а) в виде простого кратного отношения б) в процентах в) в промилле

г) в трудовых единицах измерения д) в условно-натуральных единицах измерения е) в денежных единицах измерения

3.Установите соответствие между видами относительных величин