Описание лабораторной установки и вывод расчетных формул

Установка, с помощью которой проводится изучение ферромагнитных свойств вещества, схематически изображена на рис. 8.5. На тонкий длинный стержень испытуемого материала намотаны две обмотки: намагничивающая с числом витков N₁ и измерительная с числом витков N₂. По намагничивающей обмотке через резистор с сопротивлением R₁ пропускают переменный ток I₁, величину которого можно изменять, подавая различное напряжение на трансформатор Тр от ЛАТРа.

Напряженность поля, создаваемого током I₁ в намагничивающей обмотке,

, (8.7)

где l – длина намагничивающей обмотки (она равна длине образца).

Падение напряжения на резисторе с сопротивлением R₁

. (8.8)

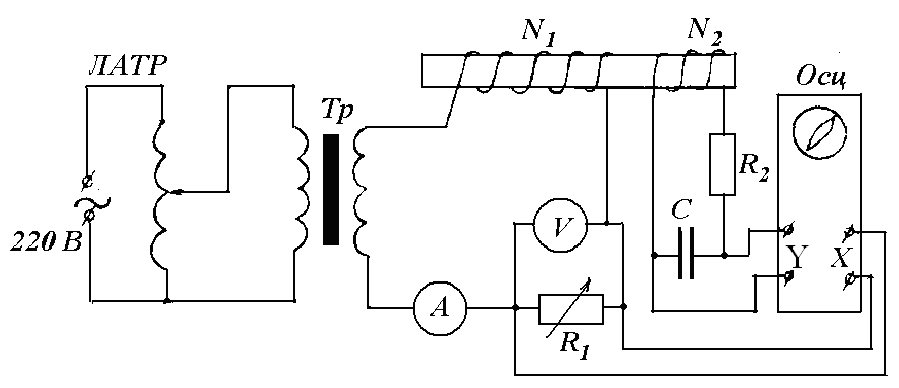
Рис. 8.5.

Из уравнений (8.7) и (8.8) имеем

. (8.9)

Если напряжение подать на горизонтально отклоняющую систему осциллографа, то отклонение луча на экране осциллографа будет, согласно формуле (8.9), пропорционально напряженности намагничивающего поляН.

В измерительной обмотке, согласно закону электромагнитной индукции, возникает ЭДС

, (8.10)

где Ф=ВS – магнитный поток через поперечное сечение S образца.

Для цепи измерительной обмотки по закону Ома можно записать:

.

Падением напряжения на сопротивлении измерительной обмотки и ЭДС самоиндукции в ней можно пренебречь ввиду их малости.

Емкость С конденсатора и сопротивления R₂ резистора, включенных в цепь измерительной обмотки, подобраны так, что . Поэтому сила тока в измерительной обмотке

/R₂

или с учетом формулы (8.10)

. (8.11)

Напряжение на конденсаторе

,

где – заряд на обкладках конденсатора.

Учитывая выражение (8.11), получим

.

Отсюда находим

. (8.12)

Следовательно, напряжение U_c пропорционально индукции магнитного поля В в образце. Оно подается на вертикально отклоняющую систему осциллографа и вызывает отклонение луча в вертикальном направлении.

Таким образом, переменный ток, протекающий в первичной (намагничивающей) обмотке, вызывает периодическое изменение как  Н, так и U_с  В по величине и направлению.

За один период синусоидального изменения тока след электронного луча на экране осциллографа опишет полную петлю гистерезиса, а за каждый последующий период – ее повторит. Поэтому на экране будет видна неподвижная петля гистерезиса.

Таким образом, для расчета по формулам (8.9) и (8.12) величин Н и В, соответствующих вершинам петель гистерезиса, необходимо найти величины напряжений иU_с. Их можно выразить через координаты вершин петель гистерезиса n_x и n_y и величины напряжений u_x и u_y, вызывающих отклонение электронного луча на одно деление в направлении горизонтальной и вертикальной осей:

= u_x n_x, U_с= u_y n_y. (8.13)

Подставляя выражения (8.13) в формулы (8.9) и (8.12), имеем

, .

Обозначим

, . (8.14)

Эти коэффициенты представляют собой масштабы осей Х и Y осциллографа. Тогда

, . (8.15)

Величины u_x и u_y зависят от степени усиления сигналов в осциллографе. Их можно определить, подавая на входы Х и Y осциллографа калиброванные напряжения и измеряя длины следа луча.

Учитывая, что длина следа луча на экране осциллографа соответствует удвоенному значению амплитудного напряжения, а вольтметр измеряет эффективное значение напряжения, для u_x и u_y получим выражения:

, , (8.16)

где l_x и l_y – длины следов луча на экране осциллографа по осям Х и Y

соответственно;

U_эф.х и U_эф.у – напряжения, подаваемые на входы осциллографа

(в данной работе U_эф.х = U_эф.у).

Коэффициент b в выражении для u_y учитывает уменьшение U_эф.у в b раз при калибровке, поскольку след луча по оси Y может не уместиться в пределах экрана осциллографа.