Лабораторные_работы_ Атомка / BOOKS / Практикум по атомной физике

из которого видно, что уровни энергии в яме конечной глубины понижаются и тем значительнее, чем больше Еn.

Переходя к количественному рассмотрению, введем обозначения

Краевые условия, обеспечивающие сшивание волновой функции, формулируются по-разному для двух типов решений: с косинусами и синусами.

1) Решения с косинусами соответствуют четным волновым функциям, удовлетворяющим соотношению y(–x) = y(x). Â

Условия сшивания при x = а

Acoska = Ce–÷a,

–Aksinka = –C÷e–÷a

приводят к трансцендентному уравнению

корни которого y1, y3, y5,… позволяют найти нечетные уровни энер-

ãèè Å1, Å3, Å5,…

2) Решения с синусами соответствуют нечетным волновым функциям, удовлетворяющим соотношению y(–x) = y(x).

Условия сшивания при x = а

–Asinka = Ce–÷a,

Akcoska = –C÷e–÷a

дают трансцендетное уравнение

71

корни которого y2, y4, y6,… позволяют найти четные уровни энер-

ãèè Å2, Å4, Å6,…

В обоих случаях связь между корнями yn и уровнями энергии Еn задается формулой

которая следует из определения (2.29) параметра у. Количество связанных состояний частицы в потенциальной

яме будет зависеть от ее глубины и ширины. Если сужать яму, оставляя неизменной ее глубину, то это приведет к уменьшению количества связанных состояний. Однако какой бы узкой и мелкой симметричная яма ни была, по крайней мере, одно связанное состояние в ней обязательно реализуется. Действительно, при а® 0 параметр у = ka, а, следовательно, и подкоренное выражение в уравнении (2.31)

также будет стремиться к нулю. А это означает, что уровень энергии Е1 неограниченно приближается к U0, оставаясь при этом меньше U0. В предельном случае бесконечно глубокой ямы U0 ® ¥ è ñ0 ® ¥. Следовательно, в соответствии с уравнениями (2.31) и (2.33)

tg ó® ¥ è ctg ó® ¥,

откуда значения корней уn могут быть выражены общей формулой: уn= pn/2, n = 1,2,3,…

Подстановка уn в (2.34) приводит к уже известному закону квантования энергии в бесконечно глубокой яме (2.31):

(не забываем при этом, что l = 2a).

Часть полученных результатов будет описывать поведение частицы также и в асимметричной потенциальной яме половинной ширины а, с бесконечно высокой левой стенкой (рис. 2.14). В этом случае на бесконечно высокой стенке (при х = 0) волновая

72

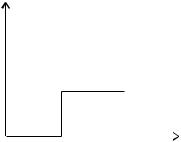
функция должна обращаться в нуль. Следовательно, граничным условиям на левой стороне удовлетворяют лишь решения с не- четными волновыми функциями, которым соответствуют уровни

Одномерная асимметричная потенциальная яма с бесконеч- но высокой стенкой представляет собой непосредственный практический интерес, поскольку к ней сводятся некоторые реальные трехмерные задачи на движение частицы в центральном силовом поле (например, задача о ядре дейтерия).

Линейный гармонический осциллятор. Линейным гармоническим осциллятором называют частицу, на которую действует упругая сила, т.е. сила, которая пропорциональна отклонению частицы от положения равновесия и направлена к нему:

Постоянная f носит название коэффициента упругости, или

коэффициента жесткости.

Потенциальная функция такой частицы имеет вид:

Графиком этой функции является парабола.

73

Согласно классической механике осциллятор совершает гармонические колебания с циклической частотой

В квантовой механике понятие силы не используется. Поэтому квантовый гармонический осциллятор следует определить как частицу с потенциальной функцией (2.38). При этом силовую постоянную f обычно выражают через частоту колебаний и массу частицы с помощью формулы (2.39). Тогда выражение для потенциальной функции принимает вид:

Подставив в стационарное уравнение Шредингера потенциальную функцию (2.40), мы получим окончательную формулировку квантово-механической задачи для линейного гармони- ческого осциллятора:

Это уравнение имеет физически приемлемые решения (которым соответствуют конечные, однозначные и непрерывные волновые функции) при значениях энергии Е, равных

Иначе говоря, последняя формула (2.42) определяет собственные значения энергии линейного гармонического осциллятора.

Собственные функции шn имеют более сложную математи- ческую структуру, чем в случае прямоугольной ямы. Функция шn представляет собой произведение функции Гаусса е–ó2/2 на полиномы Чебышева-Эрмита n-ой степени Рn(ó):

Здесь введено обозначение:

74

à Ñn есть нормирующий множитель. Для первых трех состояний полином Рn(у) имеет вид:

Функция Гаусса обеспечивает стремление волновой функции к нулю при x ® ¥. Полином Рn имеет n корней, следовательно, волновая функция имеет n узлов. Таким образом, волновая функция колеблется внутри классически разрешенной области (Е > U) и затухает по гауссовому закону там, где Е < U. Однако колебания волновой функции не являются гармоническими, как это имеет место в случае прямоугольной ямы.

Упражнение

Практической частью данной лабораторной работы является численное решение уравнения Шредингера для случаев прямоугольной потенциальной ямы конечной глубины (I) и линейного гармонического осциллятора (II). Ранее было рассмотрено аналитическое решение стационарного уравнения Шредингера для случая частицы, находящейся в прямоугольной потенциальной яме. Возможно, однако, и численное решение этой задачи, которое удобнее всего выполнить с помощью компьютера, снабженного графическим дисплеем. Следует заметить, что численный метод решения является универсальным, т.е. может быть реализован для потенциальной ямы любой формы, в то время как аналитически решаются лишь некоторые задачи.

Численное решение будем проводить в безразмерных единицах, при которых постоянная Планка и масса частицы полагаются равными единице, т.е.

D = m = 1.

В этих единицах стационарное уравнение Шредингера (2.3) принимает вид:

Поскольку стационарное уравнение Шредингера является уравнением второго порядка, то для получения единственного решения при определенном значении параметра Е необходимо, вообще говоря, задать два краевых условия. Задание краевых условий упрощается в случае симметричных потенциальных функций, удовлетворяющих условию

75

При этом оказывается, что функция ш(х) обладает определенной четностью. Для четных решений ш(–х)= ш(х), а для нечетных ш(–х) = –ш(х). Определенная четность волновой функции позволяет задать значения ш и ш´при х=0. В случае четных решений ш(0) = const и ш´(0) = 0. Для нечетных решений, наоборот, ш(0) = 0, а ш´(0) = const. Существенно, что выбор констант является достаточно произвольным и осуществляется из соображения удобства отображения волновых функций на экране дисплея.

Существует много методов численного решения дифференциальных уравнений. Ограничимся самым простым из них — алгоритмом Эйлера-Кромера. Он реализуется следующим образом.

1. Область изменения х разбивается на отрезки длиной Dõ. Dх называется величиной шага (или размером шага). Координату начала первого отрезка обозначим х0. Тогда координата конца i-го отрезка будет

õi = x0+iDx, где i принимает значения от 1 до N.

2.Задается четность функции и тем самым значения

ø(x0)=ø0 è ø´(x0)=ø´0 ïðè õ0=0.

3.Задается начальное приближение для энергии Е.

4.С помощью уравнения Шредингера вычисляется вторая производная в начале первого отрезка:

ø´´0 = 2[U(õ0) – Å]ø0.

5. Найденное значение ш´´ используется для вычисления первой производной и волновой функции в конце первого отрезка:

ø´1= ø´0+ ø´´0Dõ,

ø1= ø0 + ø´1Dõ.

6.Координата увеличивается на величину шага х1= õ0 +Dõ

èвычисляется ш´´(х) в начале второго отрезка

ø´´1= 2[U(õ1) – Å]ø1, а с помощью ш´(х) и ш(х) в конце второго

ø´2 = ø´1 + ø´´1Dõ,

ø2= ø1+ ø´2Dõ.

7. После очередного увеличения координаты на величину шага проводятся вычисления по этой же схеме для третьего

76

отрезка и так далее — до тех пор, пока координата не превысит заранее заданное значение либо волновая функция ш(х) не начнет расходиться.

8. Изменяют величину Е, после чего повторяют п.п. 2–7 вычислительной процедуры.

Таким образом, особенностью алгоритма Эйлера-Кромера является то, что вторая производная вычисляется в начале отрезка Dх, а первая производная и волновая функция — в конце.

Величину энергии Е изменяют до тех пор, пока при значе- нии Е чуть меньше предыдущего волновая функция не будет расходиться в одном направлении, а при значении Е чуть большего предыдущего — в противоположном направлении. Ширину этой «вилки» сужают настолько, чтобы она сравнялась с требуемой точностью определения собственного значения Е.

Следует отметить, что невозможно получить численное решение для функции ш, которое не расходилось бы при больших значениях х. Однако на заданном отрезке всегда можно вычислить ш с требуемой точностью, выбрав достаточно малый шаг.

Предлагаемый численный метод обеспечивает условия физической приемлемости решений стационарного уравнения Шредингера, т.е. их однозначности, непрерывности, гладкости и конечности. Однозначность обеспечивается выбором значе- ний ш(х) и ш´(х) при х = 0. Непрерывность и гладкость «автоматически» обеспечиваются самим вычислительным алгоритмом. Конечность обеспечивается выбором таких ш(х), которые не расходятся при возрастании координаты.

В данной лабораторной работе осуществляется численное решение стационарного уравнения Шредингера для двух разных потенциальных функций: одна из них соответствует прямоугольной потенциальной яме конечной глубины, а вторая — бесконечно глубокой параболической яме (гармоническому осциллятору).

I. Прямоугольная потенциальная яма конечной глубины. Для решения этой задачи предназначена программа на Бейсике «А11». В качестве входных параметров задаются глубина U0 и полуширина ямы а, четность волновой функции, величина шага Dх и предполагаемое значение энергии Е. Порядок работы с программой нетрудно понять из подсказок, которые появляются на экране во время работы. Рекомендуемый размер шага Dõ = 0,01.

Удобнее всего начать с поиска собственной функции и собственного значения энергии Е1 основного состояния. Собственная функция этого состояния состоит из одной полуволны и не

77

имеет ни одного узла. Начальное приближение энергии можно выбрать с помощью формулы (2.45) для бесконечно глубокой ямы, которая в случае безразмерных единиц (D = m = 1) принимает вид:

(Подумайте, в какую сторону будет отличаться собственное зна- чение энергии для ямы конечной глубины от значения, задаваемого этой формулой.)

Исходные приближения для второго и последующих уровней энергии можно найти с помощью соотношения:

Собственные значения энергии следует вычислять с точностью до трех десятичных знаков. Поиск собственного значения завершается подачей команды CONT, после которой появляется изображение уровня энергии внутри потенциальной ямы.

Если в процессе выполнения работы на экране монитора появляется слишком много перекрывающихся графиков, затрудняющих дальнейший поиск решений, рекомендуется отработать команду GOTO400, после выполнения которой все графики исчезнут. Для восстановления графика, который выводился непосредственно перед подачей этой команды, достаточно нажать клавишу «ВК» или «ВВОД». Другие нужные графики восстанавливаются после набора на клавиатуре соответствующих значений Е. Во всех случаях набор цифр необходимо завершать нажатием клавиши «ВК» или «ВВОД».

В конечном счете требуется найти собственные функции и собственные значения для всех связанных состояний. Как уже отмечалось, функции ш(х) проникают своими экспоненциальными «хвостами» за пределы ямы, т.е. в запрещенную класси- ческой механикой область, в которой Е < U0. Предлагается оценить глубину проникания Dl, измерив с помощью миллиметровой линейки непосредственно на экране монитора расстояние от края ямы до точки, где график волновой функции сливается с осью х. На основе этих оценочных измерений следует сформулировать качественную зависимость глубины проникания от положения уровня энергии относительно верха ямы.

78

Некоторые из найденных решений будут одновременно являться и решениями для асимметричной ямы с бесконечно высокими стенками при х = 0, но с теми же значениями параметров а и U0. Необходимо выбрать эти решения.

От ямы с безразмерными параметрами, содержащей частицу безразмерной единичной массы, достаточно просто перейти к яме, в которой находится реальная частица, например, электрон.

Из математической структуры уравнения Шредингера (2.3)

видно, что величина 2m E L2 , где Е и L представляют собой

D 2 k k ê ê

характерные значения энергии и ширины потенциальной ямы, является безразмерной. Поэтому эта величина должна иметь для данной задачи одно и то же значение во всех системах единиц. Отсюда, в частности, следует соотношение между параметрами ямы U0 è à, U0á è àá, выраженными в системных единицах и безразмерных единицах (определяемых из условия D = m = 1):

II. Линейный гармонический осциллятор. Как и в предыдущем случае, решение осуществляется в безразмерных единицах (D = m = 1). В этих единицах уравнение Шредингера для линейного гармонического осциллятора (2.41) записывается так:

а частота колебаний оказывается равной:

Упрощается и формула (2.52) для собственных значений энергии:

Численное решение уравнения (2.51) осуществляется с помощью программы под именем «А12», которая отличается от программы «А11» лишь потенциальной функцией, подставляемой в уравнение Шредингера. Эта программа позволяет найти собственные значения энергии и графики собственных функций линейного гармонического осциллятора. В качестве входных параметров задается жесткость связи f, величина шага Dõ,

79

четность волновой функции и предполагаемое значение энергии Е, которое дает формула (2.53). Следует иметь в виду, что собственные функции состояния с n = 0,2,4,… являются четными, а состояния с n = 1,3,5,… — нечетными.

Рекомендуемый размер шага Dх = 0,005. Диапазон выбираемых значений жесткости связи f = 0,4 ¸ 2. В остальном порядок работы с программой «А12» такой же, как и с программой «А11».

Задания к упражнению

1.Провести численное решение уравнения Шредингера для связанных состояний трех разных прямоугольных потенциальных ям, причем две из них имеют одинаковую полуширину и две — одинаковую глубину. (Параметры ямы задает преподаватель). Найти все собственные функции y, собственные значе- ния энергии Е, а также оценить глубину проникания Dl в классически запрещенную область. Для каждой ямы зарисовать графики собственных функций y, расположив их друг над другом и отметив на них координаты стенок ямы.

Изобразить качественный ход графиков y2 и объяснить их смысл. Построить в масштабе диаграммы уровней энергии для всех трех ям и выяснить, как повлияют на положение уровней ширина и глубина ямы.

Сравнить найденные значения уровней энергии с уровнями энергии бесконечно глубокой ямы той же ширины. Дать качественное физическое объяснение их различия.

Сформулировать качественную зависимость глубины проникания от положения уровня энергии относительно верха ямы

èдать ей объяснение.

2.Выяснить, какие из полученных решений являются также решениями для асимметричных потенциальных ям при тех же значениях параметров а и U0, где а — ширина асимметричной ямы.

3.Найти значения полуширины в ангстремах для «реальных» ям, удерживающих электрон, если глубина этих ям и расположение в них уровней, выраженных в электрон-вольтах, численно совпадают с соответствующими значениями для исследованных «безразмерных» ям.

4.Из условия (2.22) найти значения амплитудных коэффициентов А для бесконечно глубокой ямы.

5.Получить графики нескольких волновых функций при значениях энергии частицы, превышающей глубину потенциальной

80