Лабораторные_работы_ Атомка / BOOKS / Практикум по атомной физике

вблизи точки с координатами x, y, z в момент времени t. Век-

H

òîð j , называемый вектором плотности потока вероятности, дает информацию о движении частицы, показывая направление, в котором наиболее интенсивно перемещается вероятность,

тронов, перешедших в направлении вектора j через единич- ную площадку, перпендикулярную к нему, за единицу времени.

В связи с приведенной интерпретацией выражений (2.5) и

H

(2.6) волновую функцию ψ (r ,t) называют также амплитудой вероятности.

Отметим также, что для стационарных состояний выраже-

ния (2.5) и (2.6) не зависят от времени и, кроме того, если

H H

ψ (r ) — вещественная, то j обращается в нуль.

2.3. Оптические аналогии

Анализируя некоторую квантово-механическую задачу, полезно сопоставлять ее, с одной стороны, с соответствующей задачей классической механики, а с другой, — с задачей оптики. В классической механике аналогом будет, очевидно, зада- ча о движении частицы той же массы в силовом поле, характеризуемом той же потенциальной энергией U(r), что и в исходной квантовой. Выяснив характер движения классической частицы, можно глубже понять особенности ее квантово-меха- нического поведения. Оптическим же аналогом (для задачи с Е = сonst) служит распространение монохроматической световой волны с частотой ω = E / D в неоднородной среде, чей показатель преломления n изменяется в соответствии с соотношением

В этом легко убедиться, сопоставляя волновое уравнение оптики

51

(А — амплитуда световой волны) с уравнением Шредингера для стационарных состояний, переписанным в виде

Отметим, что импульс частицы, вычисленный согласно класси- ческой механике pêë= 2m( E − U ) , и волновое число, выражаемое в оптике через показатель преломления kîïò= ω n / c , связаны между собой (согласно (2.7)) соотношением де Бройля p= Dk . Аналогия с оптикой позволяет во многих случаях предвидеть и объяснить поведение y-функции, а следовательно, и частицы качественным образом без решения уравнений.

2.4. Одномерное движение частицы в условиях скачка потенциала

Среди квантово-механических задач выделяются своей простотой одномерные, т.е. такие, в которых U=U(x) и можно также ограничиться зависимостью y лишь от x и t. В этих задачах для стационарных состояний

уравнение Шредингера для стационарных состояний сводится к уравнению в обыкновенных производных

а в выражении (2.6) существенна только компонента

Уравнение (2.9) просто решается, когда потенциал U принимает постоянные значения в соседних областях, а на их границах испытывает скачок. Такой потенциал называется прямоугольным из-за прямых углов на его графике. Фактически в природе не существует потенциалов, которые действительно являются прямоугольными, так как это означало бы существование бесконечной силы в точках их скачков. Все же прямоугольные потенциалы дают грубое представление о многих действительных

52

системах, а простота математического выражения позволяет использовать их для некоторых выводов.

В области, где потенциал U постоянен, уравнение Шредингера для стационарных состояний (2.9) принимает вид

где А, В, А’, B’ — произвольные постоянные. Если учесть зависимость от времени (2.8), то волновая функция

Ψ ( x,t ) = Aei( kx− ω t ) + Be− i( kx+ ω t ),

где первый член описывает волну, бегущую вправо, а второй — волну, бегущую влево. При переходе от одной области к другой U меняется и, следовательно, изменяется длина волны. Существенно, что на границе между областями, как уже отмечалось, y(x) и ее первая производная dy/dx должны быть непрерывными. Это приводит к двум уравнениям связи между амплитудными коэффициентами (А и В) для соседних областей.

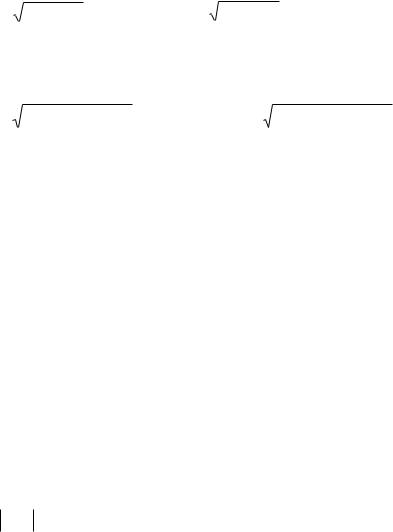
Рассмотрим случай, когда потенциал испытывает только один скачок (рис. 2.1). Предположим, что электроны с некоторой энергией Е приходят слева. С точки зрения классической физики, мы должны ожидать, что ни один электрон не будет отражаться в точке x = 0, поскольку в данной точке он испытывает действие силы, направленной вдоль направления своего движения (ускоряющей силы). Выясним теперь, что предсказывает квантовая теория для решения такой задачи.

Используем прежде всего оптическую аналогию. Электрон ведет себя в некоторой степени подобно волне, которая приходит слева и сталкивается со скачкообразным изменением показателя преломления в точке x = 0. Так же, как при падении света на поверхность раздела двух разных оптических сред, можно счи- тать, что часть волны отражается от скач- ка, а часть проходит через него. Поэтому

в области I перед скачком потенциала (x < 0) волновая функция y1(x), являющаяся решением уравнения Шредингера для

53

стационарных состояний, будет содержать два слагаемых, первое из которых соответствует падающему потоку электронов, а второе — отраженному от скачка:

В области II за скачком потенциала (x> 0) решение содержит только одно слагаемое, соответствующее прошедшей волне

ψ 2 (x) = Ceik2 x,

Постоянные А, В и С должны быть определены из граничных условий, согласно которым волновая функция и ее первая производная непрерывны в точке x = 0: y1(0) = y2(0) è (dy1/dx)(0) = (dy2/dx)(0), откуда

B и С представляют собой амплитуды отраженной и прошедшей волн, выраженные через амплитуду падающей волны А. Поскольку k2 > k1, то амплитуды отраженной и падающей волн имеют противоположные знаки, откуда следует, что при отражении от прямоугольного падения потенциала фаза волновой функции изменяется на p или, иначе говоря, происходит потеря полуволны.

Плотность потока электронов Г может быть выражена че- рез их концентрацию ne и скорость u: Ã = neu Поскольку ne ≈ ψ 2 , à õ ≈ p ≈ k òî Ã ≈ ψ 2 k. Для электронов, которые проходят вправо, коэффициент пропускания De равен отношению прошедшей плотности потока к падающей:

H

В соответствии с определением смысла вектора j коэффициенты De è Re могут быть вычислены так же, как отношения

54

De = jx,ïðîø / jx,ïàä ; Re = jx,îòð / jx,ïàä .

Äëÿ De è Re получится тот же самый результат, если электроны с энергией Е направить из области II в область I. Отличие состоит лишь в том, что отражение будет происходить без изменения фазы, поскольку в выражении (2.10) для амплитуды отраженной волны В волновые числа k1 è k2 поменяются местами.

Следует еще раз подчеркнуть, что свойство отражения частиц от резких скачков потенциала является чисто квантовомеханическим эффектом. Оно вытекает из волновых свойств материи и не может быть получено в классической физике.

В заключение сформулируем условие квантово-механичес- кой задачи, позволяющей с помощью простых методов рассмотреть квантование энергии электрона и дать качественное объяснение эффекта Рамзауэра. Речь идет о движении электрона при наличии одномерной прямоугольной симметричной потенциальной ямы (рис. 2.2). Для нее U(x) задается в виде

имеет приемлемых решений (кроме тривиального ψ (x) = 0); слу- чай а) будет детально рассмотрен в лабораторной работе ¹ 5, а случай б) — в лабораторной работе ¹ 6.

55

Лабораторная работа ¹ 5

ЭФФЕКТ РАМЗАУЭРА

Цель работы. Изучение квантовой природы эффекта Рамзауэра, экспериментальное определение критических значений энергии электронов, соответствующих максимуму и минимуму прозрачности ксенона. Вычисление глубины и ширины потенциальной ямы атома ксенона. Определение его потенциала ионизации.

Особенности упругого рассеяния электронов на атомах. В физике плазмы и газовых разрядов важную роль играют упругие столкновения электронов с атомами. От них зависит прохождение электронных пучков через газы, которое приводит к ослаблению этих пучков.

Первые исследования упругого рассеяния медленных электронов были проведены Ф.Ленардом еще в 1903 г., но количе- ственные измерения были начаты лишь в 1921 г., когда К.Рамзауэр предложил метод определения эффективного сечения рассеяния электронов.

Эффективное сечение s характеризует вероятность процесса упругого столкновения электрона с отдельным атомом и численно равно площади кружка с центром в ядре атома, при попадании в который электрон отклоняется от своего первоначального направления. Эффективное сечение связано простым соотношением с коэффициентом ослабления электронного пучка K0: K0 = = sn, где n — число атомов в единице объема газа. Нетрудно показать, что уменьшение интенсивности пучка при прохождении через слой газа толщиной х является экспоненциальным:

Пользуясь этой формулой, по измеренной величине ослабления I(0)/I(х) можно определить эффективное сечение упругого рассеяния — важную характеристику атомов и молекул. Оказалось, что оно сильно зависит от скорости электронов (рис. 2.3). По оси абсцисс откладывают величину кинетической энергии электронов, выраженную в электронвольтах.

Для большинства атомов и молекул s монотонно убывает с увеличением скорости электронов.

Однако для определенных благородных газов (аргона, криптона, ксенона) на плавный ход кривой накладывается резкий провал. При некоторой критической энергии электронов E0

56

эффективное сечение оказывается близким к нулю, вследствие чего электроны проходят через газ практически беспрепятственно. В этом заключается эффект Рамзауэра.

Эффект Рамзауэра резко противоречит классической теории рассеяния: она предсказывает монотонное уменьшение сечения с увеличением скорости электронов, связанное с уменьшением времени взаимодействия. Для интерпретации наблюдаемого рассеяния потребовалось привлечение квантовой механики. Более того, необходимость объяснить рассеяние медленных электронов дала мощный толчок развитию квантовой теории атомных столкновений.

Главным фактором, определяющим вероятность столкновения, приводящего к рассеянию, является потенциальное поле атома

мишени, создаваемое входящими в его состав электронами и ядром. В таком поле налетающие электроны изменяют направление своего движения. Важную роль играет искажение потенциального поля падающими электронами вследствие образования у частицы-мишени наведенного дипольного момента.

Поле этого наведенного диполя вызывает добавочное притяжение между электроном и атомом-мишенью и оказывается решающим для появления эффекта Рамзауэра.

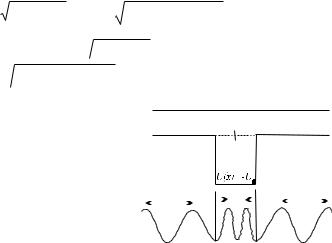
Результирующее потенциальное поле можно приближенно представить как глубокую узкую потенциальную яму, подобную приведенной на рис. 2.4 вместе с изображением атома-мишени.

Эффект Рамзауэра является следствием деструктивной интерференции электронных волн, отраженных от противоположных стенок ямы. На самом же деле она имеет не отвесные, а пологие стенки. Модель прямоугольной потенциальной она оказывается достаточно хорошим приближением не для всех атомов, а лишь для атомов тяжелых благородных газов, отличающихся наиболее компак-

тной структурой и резкой внешней границей.

57

Крутизна стенки потенциальной ямы увеличивается с возрастанием атомного номера, и именно в связи с этим эффект Рамзауэра наиболее сильно выражен у ксенона.

Точное квантово-механическое рассмотрение эффекта Рамзауэра с использованием модели трехмерной сферической потенциальной ямы является достаточно сложным. Ограничимся описанием данного явления на основе модели одномерной прямоугольной потенциальной ямы, позволяющим тем не менее выяснить его основные черты и получить приближенные коли- чественные соотношения.

Движение в области прямоугольной потенциальной ямы. Объяснение эффекта Рамзауэра. Перейдем теперь к рассмотрению движения электронов в области одномерной прямоугольной ямы глубиной U0 и шириной 2а, моделирующей взаимодействие электронов с атомами тяжелых благородных газов (рис. 2.5). Предположим, что поток электронов направлен слева направо. Согласно классической физике, ни один электрон (если Е > 0) не повернет обратно от ямы, но квантовая теория приводит к тому, что они будут отражаться от мест с резким изменением потенциала в точках х = –а и х = +a. Решения уравнения Шредингера во всех трех областях являются синусоидальными, при-

длина волны волновой функции в областях I и III оказывается

чением непрерывности ш и ш’, что позволяет выразить амплитуды отраженных и прошедших волн через амплитуду падающей волны. В конечном

счете алгебраическая структура решения оказывается довольно сложной. Иногда, однако, интерференция приводит к простому

58

области взаимодействия равен целому кратному p. Однако соответствующие минимумы сглаживаются, поскольку с увели- чением скорости возрастает влияние гармоник с l > 0.

Значение энергии, соответствующее максимуму рассеяния при эффекте Рамзауэра, может быть приближенно найдено в модели одномерной ямы из условия 4a = λ 2 + (1/ 2)λ 2 = ( 3/ 2) λ 2 . Размещение на удвоенной ширине ямы дополнительной полуволны (1/ 2)λ 2 приводит к тому, что происходит полная компенсация сдвига фаз, возникающего при отражении от передней стенки, и, следовательно, интерференционное усиление рассеянной волны. Энергию Е1, соответствующую максимуму рассеяния, можно найти из условия

Из формул (2.12) и (2.13) легко получить приближенное

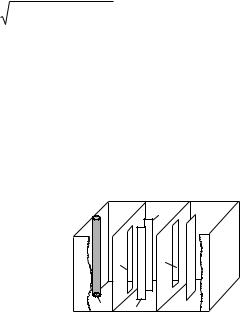
Методы экспериментального исследования эффекта Рамзауэра с помощью тиратронов. В данной работе эффект Рамзауэра на атомах ксенона исследуется с помощью тиратронов ТГЗ-0,1/1,3 (рис. 2.6) или ТП-0,1/1,3, наполненных ксено-

сетками приложить ускоряющее напряжение, величина которого меньше первого потенциала возбуждения ксенона, то ускоренные электроны, пройдя щель 3, далее в пространстве между второй сеткой 4 и щелью 5 движутся с постоянной скоростью и попадают на анод 6. На всем пути электроны претерпевают упругие столкновения с атомами ксенона. Чем больше эффективное сечение рассеяния s, тем меньше анодный ток, поскольку

60