Лабораторные_работы_ Атомка / BOOKS / Практикум по атомной физике

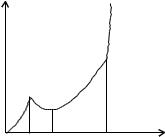
рассеянные электроны не падают на сетки и поглощаются ими. Изменяя ускоряющее напряжение, можно по точкам построить вольт-амперную характеристику (рис. 2.7).

ронными ударами. Появление в процессе ударной ионизации положительных ионов приводит к частичной компенсации объемного отрицательного заряда возле катода и уменьшению запирающего действия этого заряда, в результате чего ток начинает заметно превышать значе- ние, предписываемое формулой Богуславского-Ленгмюра. Следовательно, Ei имеет смысл энергии ионизации наполняющего тиратрон ксенона.

Другой метод исследования эффекта Рамзауэра основывается на осциллографировании анодного тока при подаче на сетку периодически изменяющегося напряжения. В данной работе используется синусоидальное напряжение звуковой частоты, которое создает пульсации тока в положительные полупериоды. В отрицательные полупериоды ток через тиратрон не течет.

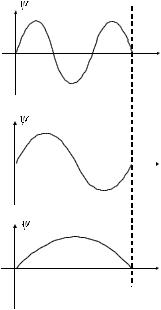
Пока амплитудное значение напряжения в вольтах не превышает величину Е0, выраженную в электронвольтах, пульсация тока имеет наиболее простую, приблизительно синусоидальную форму (рис. 2.8a). Дальнейшее увеличение амплитуды напряжения приводит к появлению на возрастающей и ниспадающей ветвях пульсации тока четко выраженных пиков Рамзауэра, появляющихся в те моменты времени, когда напряжение проходит через значение Е0. Как только амплитудное значение напряжения становится больше величины Е1, в середине пульсации вместо минимума начинает формироваться максимум (рис. 2.8б, в).

61

Превышение амплитудным значением напряжения величи- ны энергии ионизации Еi приводит к резкому излому перед серединой пульсации (рис. 2.8г), обусловленному ионизационным усилением тока, механизм которого рассмотрен выше. Необходимо отметить, что ионизационное усиление тока не прекращается моментально с прекращением процесса ионизации, а происходит еще на протяжении времени, необходимого для рекомбинации ионов и их исчезновения из межэлектродного пространства.

Ïèêè Рамзауэра

Ðèñ. 2.8.

Поэтому, если частота ускоряющего напряжения превышает некоторое значение, при котором интервал времени t0i (см. рис. 2.8г) между появлением значения напряжения Е0 è Ei оказывается меньше характерного времени рекомбинации t, то будет происходить ионизационное усиление рамзауэровского пика на ниспадающей ветви осциллограммы анодного тока. В результате пульсация тока приобретает асимметричную форму.

Очевидно, амплитудные значения напряжений, при которых осциллограммы пульсации имеют форму, промежуточную между а и б, б и в, в и г (см. рис. 2.8), будут равны соответ-

ственно Е0, E1, Ei.

Определив Е0 è E1, можно по формуле (2.14) вычислить глубину потенциальной ямы, а затем по формуле (2.13) — ее радиус а.

Упражнение

Экспериментальная установка (рис. 2.9) предусматривает возможность использования рассмотренных выше методов исследования эффекта Рамзауэра. Она состоит из блока для подключения тиратронов, вольтметра и микроамперметра, звукового генератора ГЗ-33 и осциллоскопа.

Когда переключатель Т2 на блоке тиратронов находится в положении «=», на сетку тиратрона подается постоянное напряжение

62

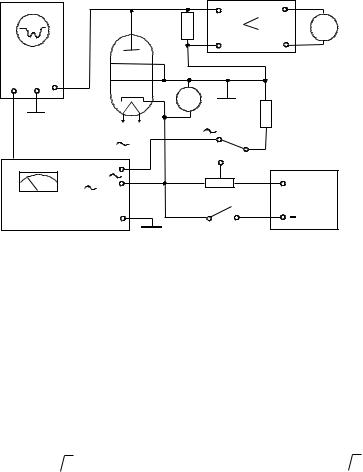
от стабилизированного источника питания, причем величину этого напряжения можно регулировать потенциометром К1, а измерять вольтметром V =.

Ðèñ. 2.9

Поскольку анодный ток весьма мал, то его непосредственное измерение затруднено. С целью упрощения процедуры измерения тока в схему введен усилитель, собранный на основе микросхемы, позволяющий обходиться обычным микроамперметром mA.

Если же переключатель T2 перевести в положение «~», на сетку тиратрона будет поступать переменное синусоидальное напряжение от звукового генератора. Частоту и амплитуду напряжения можно изменять ручками, находящимися на лицевой панели прибора. Вольтметр, встроенный в генератор, позволяет измерять эффективное значение переменного напряжения

Uýô, которое в 2 раз меньше амплитудного Uàìïë: Uàìïë = 2 Uýô. Напряжение плавно регулируется ручкой «регулировка выхо-

да» от нуля до значения, равного большему пределу шкалы вольтметра (соответствующего множителю 2). Изменение пределов регулировки напряжения осуществляется переключением ручки «пределы шкал, ослабление».

Осциллографирование анодного тока тиратрона проводится с помощью осциллоскопа, на вход У которого подается падение

63

напряжения с резистора RЗ, включенного в анодную цепь, а линейная непрерывная развертка синхронизирована напряжением задающего генератора.

Работу удобнее начинать с осциллографических исследований. Они позволяют сразу же получить общее представление о форме вольт-амперной характеристики, быстро найти напряжения, характеризующие эффект Рамзауэра и процесс ионизации. Для этого тумблеры на блоке тиратронов следует поставить в нужные положения. После прогрева приборов (в течение 10 мин) можно приступить к наблюдениям и измерениям. Плавно увеличивая напряжение ручкой «рег. выхода», наблюдать появление осциллограммы анодного тока. Ручками осциллоскопа «ча- стота плавно» и «синхронизация» добиться того, чтобы осциллограмма была неподвижной, а на экране разместилось 1–2 ее периода. Проследить за эволюцией осциллограммы, доведя напряжение до 10В.

Измерить эффективные значения напряжения Uýô0, Uýô1, Uýôi, соответствующие энергиям электронов E0, E1, Ei. Измерения следует производить на тех пределах регулировки напряжения, на которых отсчет вольтметра составляет не менее половины его шкалы.

Основываясь на асимметрии осциллограммы, можно произвести экспериментальную оценку времени рекомбинации ионов. Сохраняя неизменной величину напряжения на таком уровне, чтобы его амплитуда заметно превышала Ei, путем перестройки звукового генератора плавно увеличивают частоту, пока не появится асимметрия рамзауэровских пиков. Измеренный на осциллограмме интервал t0i даст при этом значение времени рекомбинации tðåê.

После завершения осциллографических исследований вклю- чить осциллоскоп и приступить к измерениям на постоянном токе. Для этого необходимо переключить тумблеры на блоке тиратронов. Увеличивая потенциометром R1 напряжение на сетке, снять показания микроамперметра mA. В областях более быстрого изменения тока отсчеты следует делать чаще. Данные занести в таблицу, которая используется для построения вольтамперной характеристики. По ней найти значения E0 è E1, определяющие эффект Рамзауэра.

В установке предусмотрена также возможность осциллографического наблюдения вольт-амперной характеристики (см. рис. 2.7) и измерения ее особых точек: на сетку тиратрона подается пилообразное напряжение от развертки осциллографа.

64

Напряжения, соответствующие энергиям электронов E0, E1, Ei, измеряются с помощью специального электронного блока, который вырабатывает короткий импульс (метку), накладываемый на осциллограмму. Путем изменения напряжения смещения импульс выводят на нужную точку осциллограммы. Напряжение смещения при этом в точности совпадает с напряжением данной точки вольт-амперной характеристики, и его измеряют с помощью вольтметра.

Как и в работе по определению потенциала ионизации атома ртути, наличие контактной разности потенциалов между катодом и сеткой тиратрона завышает полученные из вольтамперной характеристики напряжения на несколько десятых вольта. Поэтому для учета контактной разности необходимо вводить соответствующую поправку.

Для вычисления параметров потенциальной ямы, соответствующей взаимодействию электрона с атомом ксенона, следует использовать средние арифметические значения E0 è E1, найденные разными методами.

Задания к упражнению

1.Выполнить осциллографическое исследование эффекта Рамзауэра для атомов ксенона на частоте 300Гц, в ходе которо-

го определить критические значения энергии электронов E0 è E1, а также энергию ионизации Ei (с учетом контактной разности потенциалов). Зарисовать с экрана осциллоскопа типичные осциллограммы анодного тока.

2.Увеличивая частоту до нескольких тысяч герц, проследить влияние частоты на форму осциллограммы. Зарисовать типичные осциллограммы. Объяснить происхождение асимметрии рамзауэровских пиков. Оценить время рекомбинации ионов

âтиратроне.

3.Произвести измерения, необходимые для построения вольт-амперной характеристики. Построить вольт-амперную характеристику и с ее помощью определить критические зна-

чения энергии электронов E0, E1 è Ei. Ввести поправку на контактную разность потенциалов.

4.Найти глубину U0 и радиус а потенциальной ямы, соответствующей взаимодействию электрона с атомом ксенона, ис-

пользуя средние арифметические значения E0 è E1, определенные разными методами.

65

Контрольные вопросы

1.Понятие эффективного сечения упругого столкновения

èего связь с коэффициентом ослабления.

2.В чем состоит сущность эффекта Рамзауэра?

3.За счет чего создается потенциальное поле атома-мише- ни, приводящее к его взаимодействию с налетающим электроном?

4.Квантово-механическое описание движения в области прямоугольной потенциальной ямы.

5.Объяснение эффекта Рамзауэра на одномерной модели. Условие отсутствия упругого рассеяния электронов.

6.Вывести приближенное соотношение, связывающее глу-

бину потенциальной ямы U0 c энергиями минимального и максимального рассеяния электронов E0 è E1.

7.Какие особенности конструкции тиратрона приводят к влиянию упругого рассеяния электронов на анодный ток?

8.Объяснить особенности вольт-амперной характеристики тиратрона, связанные с эффектом Рамзауэра.

9.Объяснить сущность осциллографического метода исследования эффекта Рамзауэра.

10.Объяснить осциллографический метод определения энергии ионизации ксенона.

11.В каких условиях появляется асимметрия рамзауэровских пиков по интенсивности и в чем ее причина?

12.Рассказать об устройстве экспериментальной установки для исследования эффекта Рамзауэра.

Лабораторная работа ¹ 6

КВАНТОВАНИЕ ЭНЕРГИИ ЛОКАЛИЗОВАННОЙ ЧАСТИЦЫ

Цель работы. Знакомство с одним из методов численного решения стационарного уравнения Шредингера; выявление характерных особенностей физически приемлемых решений; изучение влияния формы потенциальной ямы на собственные функции и собственные значения энергии для связанных состояний.

66

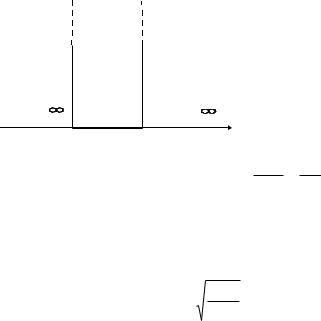
Частица в прямоугольной потенциальной яме. Вначале рассмотрим случай прямоугольной потенциальной ямы с бесконеч- но высокими стенками. На этом самом простом примере лучше всего можно проследить, каким образом уравнение Шредингера приводит к квантованию энергии.

Микроскопическая частица массой m, обладающая некоторой энергией Е, находится в поле, которое характеризуется следующим образом: в области от х = 0 до х = l потенциальная энергия U(х) постоянна и равна нулю; на границах же области U(x) скачкообразно возрастает до бесконечности (рис. 2.10).

При таких условиях можно

Нетрудно убедиться, что уравнению (2.16) удовлетворяет функция

имеет смысл волнового числа. Функция (2.17) удовлетворяет также краевому условию на левой стенке, т.е. при х = 0. Однако обращение ее в нуль на правой стенке, т.е. ø (l) = Asin kx = 0, возможно лишь при значениях волнового числа k =kn, удовлетворяющих соотношению

knl=pn,n=1,2,3,.... (2.19)

Именно при этих значениях k и получаются физически приемлемые решения уравнения Шредингера, которым отвечают собственные функции

67

размещается целое число полуволн y-функции.

Рассмотрим теперь более сложный случай симметричной прямоугольной ямы конечной глубины. Как и в предыдущем случае, будем считать, что потенциальная энергия внутри ямы U(x) = 0. За пределами ямы потенциальная энергия всюду имеет одно и то же значение U(x) = U0 (рис. 2.12). В случае, когда частица массой m находится внутри ямы (связанные состояния), ее полная энергия Е должна быть меньше U0: Å < U0.

68

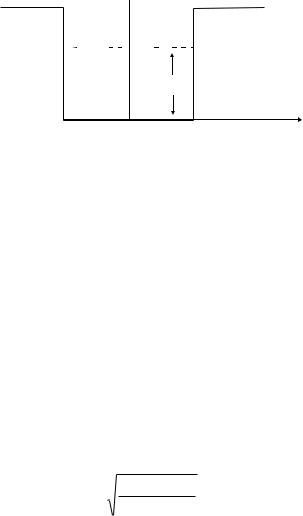
Начало координат выберем посередине ямы, тогда координаты стенок будут –а и +а. Параметр а является полушириной ямы:

U

Волновая функция y(x) для области внутри ямы может быть найдена с помощью прежнего уравнения (2.25). Однако в связи с выбором начала координат не на краю, а посередине ямы, возможные решения уже не исчерпываются выражением (2.17), (т.е. синусами), поскольку теперь при x = 0 будут не только узлы, но и пучности волновой функции. Чтобы при x = 0 полу- чить пучности, среди решений должны быть косинусы того же аргумента kx.

Далее, в отличие от бесконечно глубокой ямы, волновая функция за пределами ямы и на ее стенках уже не обращается в нуль, а должна удовлетворять уравнению Шредингера при U(x) = U0.

Физически приемлемым решениям этого уравнения отвечают затухающие экспоненты

Чем меньше энергия частицы Е отличается от глубины ямы (не забываем, что Е < U0), тем дальше, в соответствии с (2.25), волновые функции своими «экспоненциальными хвостами»

69

выходят за пределы ямы. Графики нескольких волновых функций приведены на рис. 2.13.

димости удовлетворения краевых условий для волновой функции. Понятно, что закон кванто-

вания энергии оказывается иным, чем для бесконечно глубокой ямы. Для качественного сравнения уровней энергии в ямах конечной и бесконечной глубины можно пользоваться следующими соображениями. Проникание волновой функции за пределы ямы конечной глубины фактически означает увеличение ее эффек-

причем эффективная ширина неодинакова для разных уровней энергии: чем выше уровень Еn, тем эффективная ширина больше (см. рис. 2.13).

Если в формулу (2.21) вместо геометрической ширины ямы подставить ее эффективную ширину, то мы придем к соотношению

70