Порядок виконання роботи

Рис. 2.

Прилад являє собою вертикально розташований скляний циліндр, який наповнено досліджуваною рідиною і має зовнішню шкалу (рис.2). По шкалі визначається відрізок шляху l рівномірного падіння кульки, час руху t якого вимірюється секундоміром.

Перед опусканням кульки в рідину необхідно декілька разів виміряти діаметр кульки мікрометром.

За допомогою пінцета занурити кульку в рідину вздовж осі циліндра. Відлік часу починати тоді, коли кулька знаходиться навпроти обраної верхньої мітки шкали „m”. Обрана верхня мітка повинна бути розташована на 5-6 см нижче рівня рідини. У момент проходження кульки через верхню мітку включити секундомір. При проходженні кульки через нижню обрану мітку „n” секундомір зупинити. У такий спосіб визначається час t проходження кулькою шляху l при рівномірному русі кульки. Результати вимірювань і обчислень занести до таблиці 1.

Таблиця 1

Результати вимірювань та обчислень

№ п/п	Діаметр кульки di, м	Відрізок шляху li, м	Час падіння кульки ti, с	Швидкість падіння , м/с	Густина , кг/м3		Коефіцієнт в’язкості <>,
					кульки	рідини
1
2
3
4
5
–

За вказівкою викладача визначити похибки вимірювань фізичних величин.

Питання для самоперевірки

1. Записати і сформулювати закон Архімеда.

2. Записати і сформулювати закон Стокса.

3. Записати формулу, за якою в лабораторній роботі визначається коефіцієнт динамічної в’язкості рідини .

4. Вивести одиницю вимірювання коефіцієнта динамічної в’язкості .

5. Від чого залежить коефіцієнт в’язкості рідини ?

6. Записати формулу, що зв’язує коефіцієнт динамічної в'язкості  з коефіцієнтом кінематичної в'язкості .

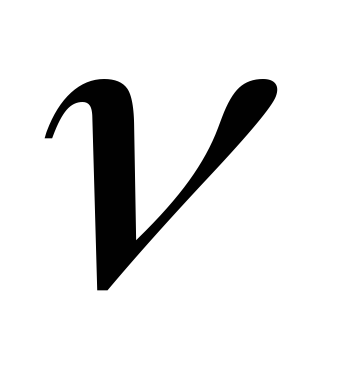7. Вивести одиницю вимірювання коефіцієнта кінематичної в’язкості v.

8. Які сили діють на кульку, що падає у в’язкій рідині ?

9. Чому, починаючи з деякого моменту часу, кулька рухається в рідині рівномірно ?

10. Як зміниться швидкість руху кульки в рідині при збільшенні діаметру кульки ?

Лабораторна робота № 7 дослідження електростатичного поля

Мета роботи: експериментально дослідити конфігурацію електростатичного поля між металевими електродами.

Прилади та обладнання: джерело постійної напруги, пластина з електродами, вольтметр, гальванометр, потенціометр, металевий зонд, перемикач, з’єднувальні провідники, папір.

Теоретичні відомості

Нерухомий електричний заряд створює у просторі електростатичне поле, яке проявляється за силовою дією на вміщений у будь-яку точку поля інший заряд.

Електростатичне поле має дві характеристики – силову та енергетичну. Кількісна силова характеристика називається напруженістю електростатичного поля . Ця фізична величина є векторною і в даній точці електростатичного поля чисельно дорівнює силі, з якою поле діє на одиничний позитивний точковий зарядq₀, що знаходиться в даній точці поля:

. (1)

Електростатичне поле зручно зображувати у вигляді силових ліній. Густина силових ліній характеризує числове значення напруженості, а дотичні до них у кожній точці збігаються з напрямом вектора напруженості .

Силові лінії починаються на позитивних зарядах і закінчуються на негативних, вони ніде не перетинаються, тому що в кожній точці поля вектор має лише один напрямок.

Енергетичною характеристикою електростатичного поля є потенціал. Він чисельно дорівнює роботі A, яку виконують сили поля при перенесенні одиничного позитивного точкового заряду з даної точки поля в нескінченість:

. (2)

Різниця потенціалів (напруга) між двома точками поля визначається роботою по переміщенню одиничного позитивного точкового заряду з однієї точки простору в іншу:

. (3)

Геометричне місце точок з однаковим потенціалом називається еквіпотенціальною поверхнею. Лінії напруженості в кожній точці ортогональні до еквіпотенціальних поверхонь. Дійсно, при переміщенні заряду вздовж еквіпотенціальної поверхні робота, яка згідно (3) визначає різницю потенціалів між двома точками поля, дорівнює нулю (потенціал не змінюється). З іншого боку за визначенням A=Flcos=0. У цій формулі переміщення l відбувається вздовж еквіпотенціальної поверхні, а сила спрямована вздовж силової лінії. Обидві ці величини (l і ) не дорівнюють нулю, таким чином, cos = 0 і відповідно  = 90⁰.

Зв'язок між напруженістю електростатичного поля та потенціалом описується співвідношенням:

, (4)

де – градієнт, який пов’язує скалярну величину (потенціалφ) з векторною (напруженість ). Знак "–" вказує на те, що вектор напруженості електростатичного поля спрямований в бік зменшення потенціалу.

На рис. 1 зображений переріз площиною рисунка картини розподілу еквіпотенціальних поверхонь і силових ліній для електростатичного поля двох протилежно заряджених кульок. У цьому випадку за напрям зміни потенціалу вибираємо напрям силової лінії.

Рис. 1.