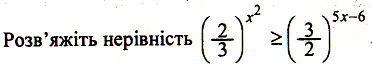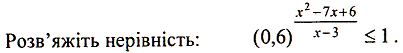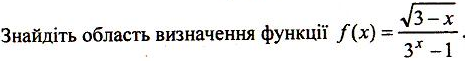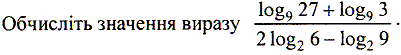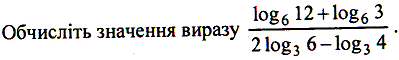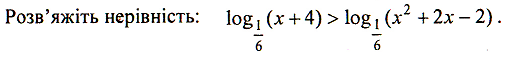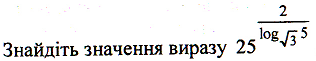Хід уроку

І. Організаційний момент. (5 хв)

ІІ. Перевірка домашнього завдання. (15 хв)

ІІІ Повідомлення теми, формулювання мети і основних завдань (5 хв)

ІV. Викладання матеріалу.(53 хв)

V. Домашнє завдання (2 хв)

ІV. Викладання матеріалу.

Показникові рівняння можна умовно розділити на наступні типи.

• Найпростіші: для розв’язання яких потрібно зводити до однієї основи і використовувати правило 1

• Показникові рівняння, у лівій частині яких є сума степенів з однаковою основою і показниками, які відрізняються на стале число:

Рівняння такого виду зводяться до найпростішого винесенням у лівій частині за дужки степеня з певним показником

Розв’яжіть рівняння

1).

2)

3)

4)

5) 6*3 ^х+1 – 5*3 ^х =39

6) 7 ^х – 2 ^{х +2} = 5*7 ^{х – 1} – 2 ^х-1

7) 7 ^х-1 – 5 ^х – 3*5 ^х-1 + 7 ^х = 0

• Показникові рівняння, що зводяться до квадратичних відносно показникової функції: Розв’язується шляхом заміни змінних

Розв’яжіть рівняння

1)

2)

3)

4)

5)

6)

7) 9 ^х – 12*3 ^х +27 =0

8) 7 ^{2 х -3} = 7 ^{х – 2} +6

9) 2 ^{х +1} – 3*4 ^{х – 2} =5

10) 3 ^х + 5*3 ^{2 – х} =14

11) 5 ^х + 125*5 ^–х =30

• Однорідні показникові рівняння: Рівняння виду

a₁a^2x +a₂a^xb^x + a₃b^2x = 0 називаються однорідними показниковими рівняннями. Для розв’язання такого рівняння треба ліву й праву частини рівняння поділити на a^2x або b^2x

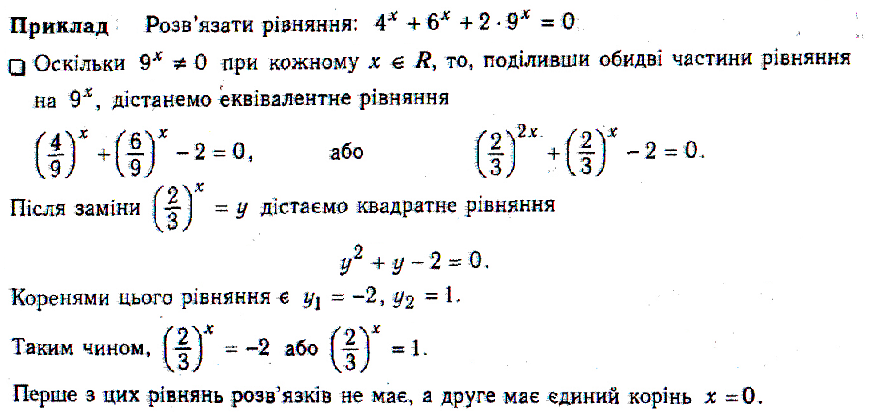
Розв’яжіть рівняння

1)

2) 4*9 ^х – 7*12 ^х + 3*16 ^х = 0

3) 3 ^2х+1 – 2*15 ^х – 5 ^{2х + 1} =0

4) 3*16 ^х + 2*81 ^х = 5*36 ^х

V . Домашнє завдання.

Розв’яжіть рівняння

1) 4^х-3 – 3*4^х-4 + 2*4^х-5 = 96

2) 9^х – 12*3^х + 27 = 0

3) 3*4^х + 2*9^х = 5*6^х

Урок № 20

Тема: Приклади розв’язування показникових рівнянь

Мета: Навчити студентів розв׳язувати показникові рівняння.

Поняття та терміни: Показникові рівняння та тотожності

Обладнання: дошка, роздатковий матеріал.

Тип уроку:комбінований.

Хід уроку

І. Організаційний момент. (5 хв)

ІІ. Перевірка домашнього завдання. (15 хв)

ІІІ Повідомлення теми, формулювання мети і основних завдань (5 хв)

ІV. Викладання матеріалу.(53 хв)

V. Домашнє завдання (2 хв)

ІV. Викладання матеріалу.

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

V. Домашнє завдання

Підготуватися до контрольної роботи

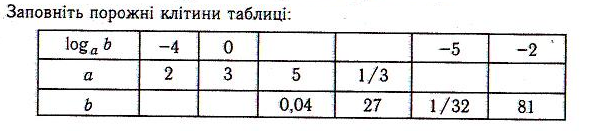
Логарифмічна функція

Урок № 22

Тема: Логарифм числа. Означення логарифма.Властивості та основні правила логарифмування. Приклади.

Мета: : Сформувати у студентів уявлення про логарифм числа, їх властивості. На прикладах проілюструвати основні правила логарифмування.

Поняття та терміни: Логарифм числа, основні правила логарифмування

Обладнання: дошка, роздатковий матеріал.

Тип уроку:комбінований.

Хід уроку

І. Організаційний момент. (8 хв)

ІІ. Актуалізація опорних знань. (5 хв)

ІІІ. Повідомлення теми, формулювання мети і основних завдань (7 хв)

ІV. Викладання нового матеріалу.(65 хв)

V. Домашнє завдання (5 хв)

ІV. Викладання матеріалу.

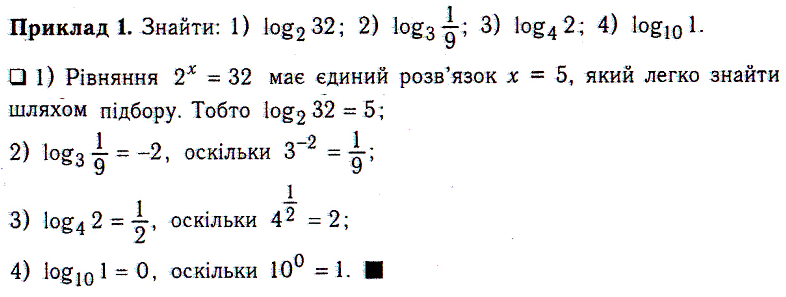
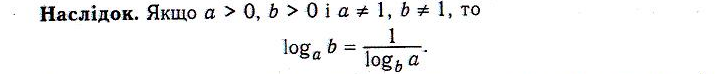
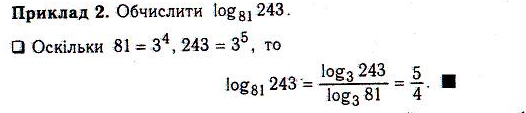
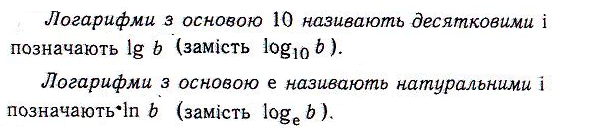
Вправи

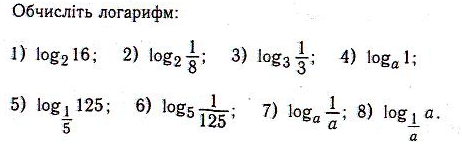
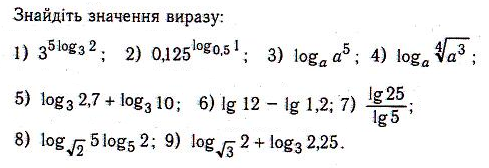
10)

11)

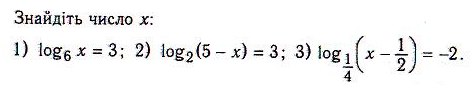
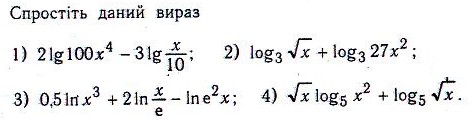
V . Домашнє завдання.

Вправа 1.2; вправа 3.2, 3.6: Вправа 4.5

Урок № 23

Тема: Логарифмічна функція. Означення логарифмічної функції, властивості та графіки логарифмічних функцій.

Мета: : Сформувати у студентів уявлення про логарифмічні функції,їх властивості та графіки.

Поняття та терміни: Логарифмічна функція, графік логарифмічної функції

Обладнання: дошка, роздатковий матеріал.

Тип уроку:комбінований.

Хід уроку

І. Організаційний момент. (5 хв)

ІІ. Перевірка домашнього завдання. (15 хв)

ІІІ Повідомлення теми, формулювання мети і основних завдань (5 хв)

ІV. Викладання матеріалу.(53 хв)

V. Домашнє завдання (2 хв)

ІV. Викладання матеріалу.

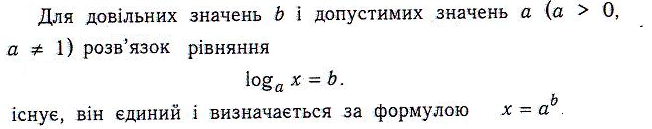
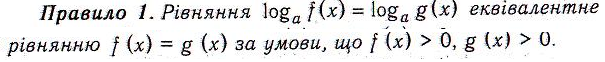
Правило2

Вправи

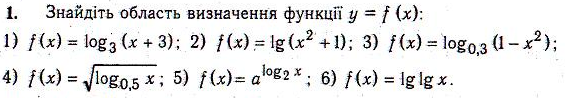
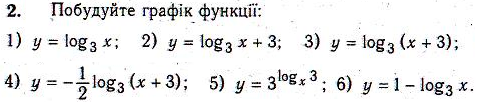
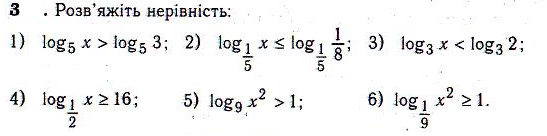
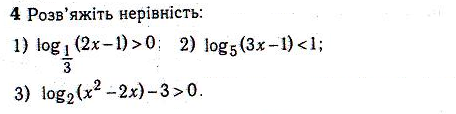
4)5)

6) 7)

V. Домашнє завдання

Приклад (1.3), (2.3) (3.2) (4.4)

Урок № 24

Тема: Логарифмічні рівняння та нерівності. Методи розв’язання логарифмічних рівнянь та нерівностей.

Мета: : Сформувати у студентів уявлення про логарифмічні нерівності, їх методи розв׳язання.

Поняття та терміни: Логарифмічні рівняння та нерівності

Обладнання: дошка, роздатковий матеріал.

Тип уроку:комбінований.

Хід уроку

І. Організаційний момент. (5 хв)

ІІ. Перевірка домашнього завдання. (15 хв)

ІІІ Повідомлення теми, формулювання мети і основних завдань (5 хв)

ІV. Викладання матеріалу.(53 хв)

V. Домашнє завдання (2 хв)

ІV. Викладання матеріалу.

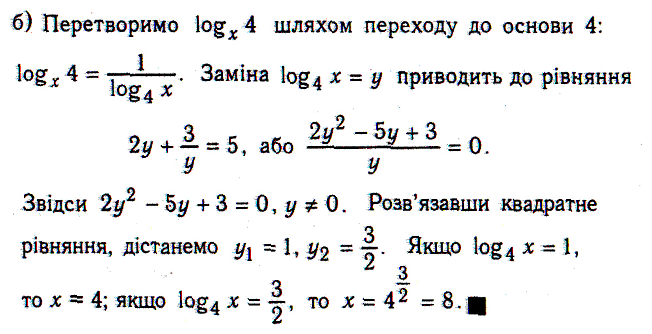
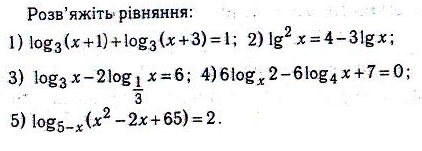
6)

7)

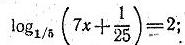
8)

9)

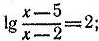
10)

11)

V. Домашнє завдання

№3, 4, 7

Урок № 25

Тема: Приклади розв’язання логарифмічних рівнянь та нерівностей.

Мета: Навчити студентів розв’язувати логарифмічні рівняння та нерівності.

Поняття та терміни: Логарифмічні рівняння та нерівності

Обладнання: дошка, роздатковий матеріал.

Тип уроку:комбінований.

Хід уроку

І. Організаційний момент. (5 хв)

ІІ. Перевірка домашнього завдання. (15 хв)

ІІІ Повідомлення теми, формулювання мети і основних завдань (5 хв)

ІV. Викладання матеріалу.(53 хв)

V. Домашнє завдання (2 хв)

ІV. Викладання матеріалу.

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

19. 

Рівняння, нерівності та їхні системи

Урок № 27

Тема: Основні види рівнянь з однією змінною. Загальні методи розв’язання.

Мета: Узагальнити знання студентів, отримані за семестр про основні види рівнянь з однією змінною та їх методи розв’язання

Поняття та терміни: Поліноміальні, показникові, Логарифмічні рівняння.

Обладнання: дошка, роздатковий матеріал.

Тип уроку:комбінований.

Хід уроку

І. Організаційний момент. (8 хв)

ІІ. Актуалізація опорних знань. (5 хв)

ІІІ. Повідомлення теми, формулювання мети і основних завдань (7 хв)

ІV. Викладання нового матеріалу.(65 хв)

V. Домашнє завдання (5 хв)

ІV. Викладання матеріалу.

Під час навчання нами були з’ясовані основні види рівнянь з однією змінною, деякі будемо розглядати пізніше. Перші рівняння, з якими ми зіштовхнулися це звичайні лінійні рівняння з однією змінною. Далі ми розглядували степеневі рівняння, але обидва типа можна поєднати в один вид рівнянь – поліноміальний. Де лінійне рівняння можна представити як степеневе рівняння зі старшим членом першої степені. Нами також були вивчені такі види рівнянь як показникові та логарифмічні, а пізніше вивчімо тригонометричні рівняння. Крім цих рівнянь існує ще один вид рівнянь, який вивчається у вищій математиці. Цей вид називається комплексні рівняння, на яких ми зупинятися не будемо. Підводячи підсумок ще раз визначимо основні види рівнянь з однією змінною які вивчили або будемо вивчати пізніше. Отже основні види рівнянь з однією змінною:

• Поліноміальні;

• Показникові;

• Логарифмічні;

• Тригонометричні.

На цій лекції ми більш детально розглянемо поліноміальні рівняння та знаходження коренів рівнянь, шляхом розкладання полінома на множники. Самим універсальним, але не завжди більш швидкий, спосіб це ділення поліном на поліном першого порядку (тобто лінійний).

Наприклад для рівняння х³-6х²+12х-8=0 ми відразу можемо сказати що коренів рівняння 3, тобто дорівнює кратності старшого члена. Щоб підібрати поліном дільник потрібно визначити на які цілі числа націло ділиться вільний член. В нашому випадку це 1, -1, 2, -2, 4, -4, 8, -8. Підставимо числа у рівняння. Числа 1 та -1 не задовольняють рівнянню, тобто 1 та -1 не є розв’язками рівняння. Число 2 задовольняє рівнянню, тобто нам потрібно поділити на (х-2) щоб отримати поліном меншого порядку. Треба зауважити, що залишку при діленні не залишилось і 2 є коренем рівняння, тобто поліном х³-6х²+12х-8 можна представити у вигляді х³-6х²+12х-8=(х-2)(х²-4х+4). Де (х-2) - це наш дільник а (х²-4х+4) - результат ділення. Далі ми отримали поліном другого степеня, тобто квадратичне, яке ми можемо розв’язати через дискримінант або за теоремою Вієта. Підводячи підсумок цього приклада, ми маємо три кореня що збігаються, тобто рівняння має корінь 2 кратності 3.

Приклад.

Знайти корені рівняння методом пониження порядку(ділення поліном на поліном)

1. х³+6х²+11х+6=0 Відповідь: (х+1)(х+2)(х+3)=0

2. 3х³+14х²+13х-6=0 Відповідь: (х+2)(х+3)( 3х-1)=0

3. 2х³-2х²-18х+18=0 Відповідь: (х+3)(х-3)( 2х-2)=0

4. 4х³-24х²+39х-14=0 Відповідь: (х-2)( 2х-1)( 2х-7)=0

5. 2х³-4х²-10х+12=0 Відповідь: (х-3)( 2х-2)(х+2)=0

6. 2х³+9х²+12х+5=0 Відповідь: (х+1)( 2х+5)(х+1)=0

7. х³-9х²+24х-20=0 Відповідь: (х-5)(х-2)(х-2)=0

8. 3х³-19х²+21х-5=0 Відповідь: (х-5)(х-1)( 3х-1)=0

9. 3х³+х²-27х-9=0 Відповідь: (х+3)( 3х+1)(х-3)=0

10. -3х³+4х²+17х-6=0 Відповідь: (х+2)( 3-х)( 3х-1)=0

11. 2х³-х²-2х+1=0 Відповідь: (х+1)(х-1)( 2х-1)=0

12. 4х³-19х+15=0 Відповідь: (х-1)( 2х-3)( 2х+5)=0

13. 3х³-х²+-48х+16=0 Відповідь: (х-4) (х4)( 3х-1)=0

14. 5х³+27х²-20х-12=0 Відповідь: (х+6)( 5х+2)(х-1)=0

15. 2х³-9х²+7х+6=0 Відповідь: (х-3)(х-2)( 2х+1)=0

16. 3х³-14х²+13х+6=0 Відповідь: (х-2)( 3х+1)(х-3)=0

17. х³-6х²+11х-6=0 Відповідь: (х-1)( х-3)(х-2)=0

18. 4х³+4х²-29х-15=0 Відповідь: (х+3)( 2х-5)( 2х+1)=0

19. 4х³+20х²+32х+16=0 Відповідь: (х+2)(х2)( 4х+4)=0

20. -3х³+7х²+18х+8=0 Відповідь: (х+1)( 4-х)( 3х+2)=0

V. Домашнє завдання.

Знайти корені рівняння методом пониження порядку(ділення поліном на поліном)

1. 3х³+5х²-3х-5=0 Відповідь: (х-1)(х+1)(3х+5)=0

2. х³+9х²+24х+16=0 Відповідь: (х+4)(х+4)(х+1)=0