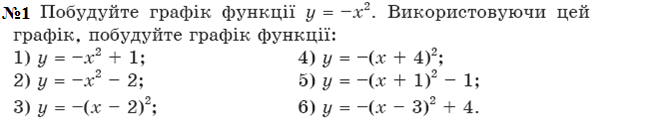2. Парність та непарність

Приклад 7

Розвязання

Приклад 8

Розвязання

Приклад 9

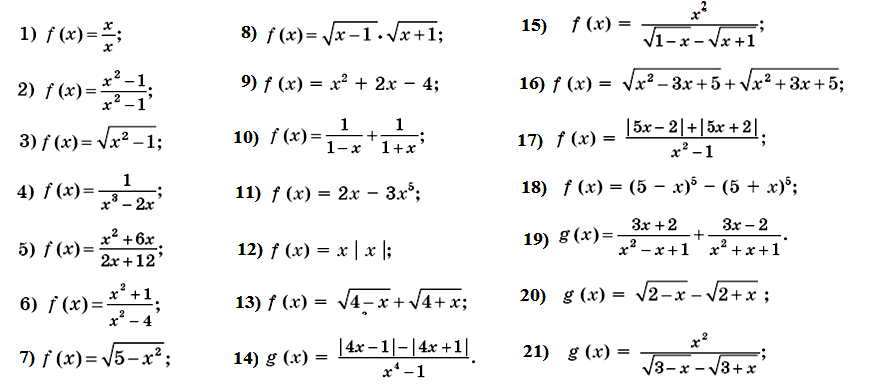
Приклад 10

;

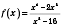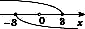
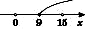
— симетрична відносно нуля. (На координатній прямій 0 позначено для того, щоб простежити, чи симетрична відносно 0.)

.

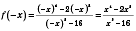Функція парна.

Приклад 11

;

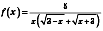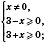
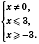
— симетрична відносно 0.

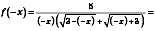
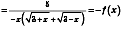
.Функція непарна.

Приклад 11

.— симетрична відносно 0. ; .

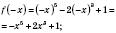Функція не є ані парною, ані непарною.

Приклад 12

.

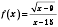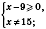
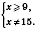
— несиметрична відносно нуля. Функція не є ані парною, ані непарною. 

VІ Домашнє завдання.

1)

2)

3)

4)

Урок № 6

Тема: Побудова графіків функцій. Приклади побудови лінійних, степеневих та тригонометричних функцій.

Мета: Сформувати уявлення студентів про графіки найпоширеніших функцій.

Поняття та терміни:Лінійна, квадратична функції, обернена пропорційність. Графік дробово- лінійної та квадратичної функції .

Обладнання: роздатковий матеріал, дошка.

Тип уроку:Комбінований.

Хід уроку

І. Організаційний момент. (5 хв)

ІІ. Перевірка домашнього завдання. (15 хв)

ІІІ Повідомлення теми, формулювання мети і основних завдань (5 хв)

ІV. Викладання матеріалу.(50 хв)

V. Домашнє завдання (5 хв)

ІV. Викладання матеріалу.

Згадаємо деякі графіки функцій які були вивчені у школі. Це лінійна функція, обернена пропорційність та квадратична функція. Кожна з них є частинним випадком степеневої функції, де степінь старшого члена у першій дорівнює 1, -1 у другій і 2 у третій. Розглянемо їх більш детально.

Іноді буває складно будувати графіки по точкам, але якщо ми знаємо як виглядає класичний графік, то шуканий графік можна отримати шляхом елементарних перетворень класичного. Розглянемо це на прикладі квадратичної функції, графіком якої є парабола, та дробово–лінійної, графіком якої є парабола.

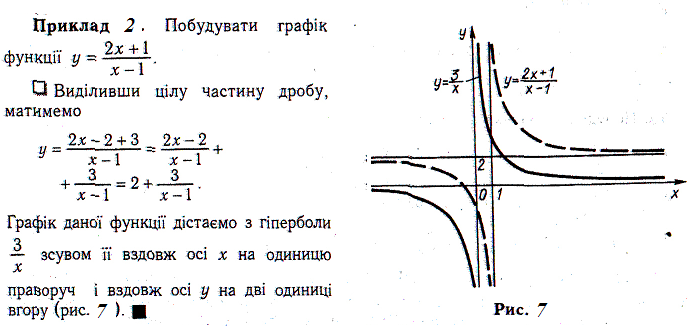
Приклад 3 Побудувати графік функції

Приклад 4 Побудувати графік функції

Приклад 5 Побудувати графік функції

Приклад 6 Побудувати графік функції

Приклад 7 Побудувати графік функції

Приклад 8 На скільки треба зсунути параболу вздовж осей х та у щоб дістати

. Тобто потрібно зсунути на 2 ліворуч і на 5 донизу

VІ Домашнє завдання.

Урок № 7

Тема: Перетворення графіків функцій.

Мета: Сформувати уявлення студентів про перетворення графіків функцій. Навчити будувати графіки функцій завдяки перетворенням елементарних функцій.

Поняття та терміни: Графік, абсциса, ордината, паралельне перенесення.

Обладнання: роздатковий матеріал, дошка.

Тип уроку:Комбінований.

Хід уроку

І. Організаційний момент. (5 хв)

ІІ. Перевірка домашнього завдання. (15 хв)

ІІІ Повідомлення теми, формулювання мети і основних завдань (5 хв)

ІV. Викладання матеріалу.(50 хв)

V. Домашнє завдання (5 хв)

ІV. Викладання матеріалу.

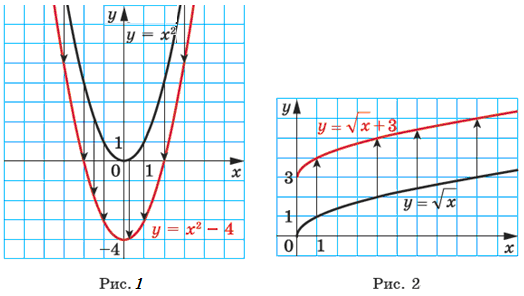
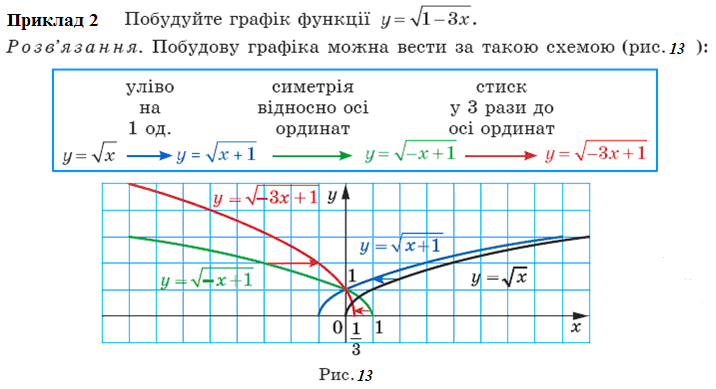
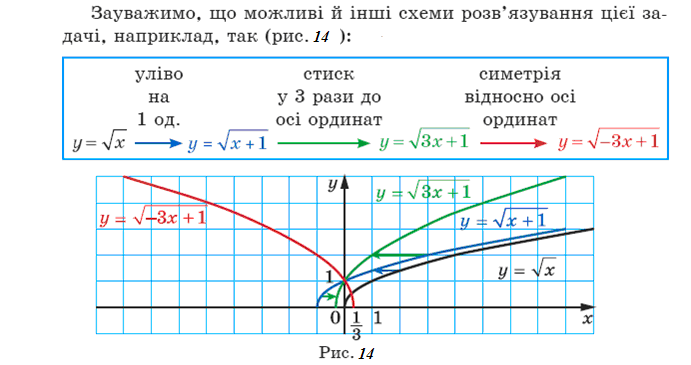
1. . Графік функції y = f (x) + b можна отримати в результаті паралельного перенесення графіка функції y = f (x) на b одиниць угору, якщо b > 0, і на –b одиниць униз, якщо b < 0.

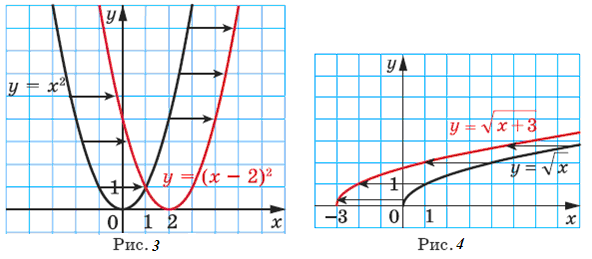
2. Графік функції y = f (x + a) можна отримати в результаті паралельного перенесення графіка функції y = f (x) на a одиниць уліво, якщо a > 0, і на –a одиниць управо, якщо a < 0.

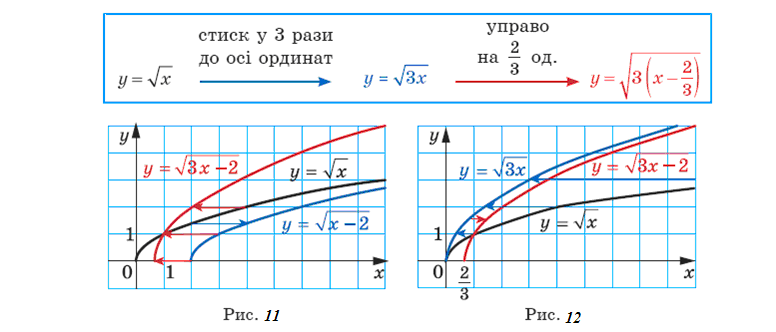
3. Графік функції y = kf (x) можна отримати, замінивши кожну точку графіка функції y = f (x) на точку з тією самою абсцисою і ординатою, помноженою на k.

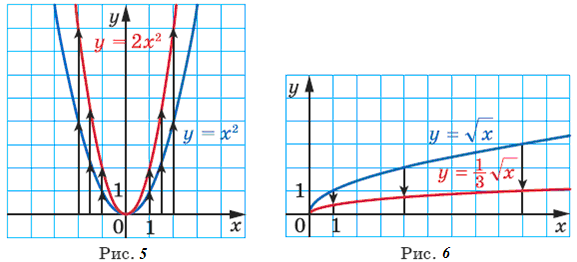
4. Графік функції y = f (kx), де k > 0, можна отримати, замінивши кожну точку графіка функції y = f (x) на точку з тією самою ординатою і абсцисою, поділеною на k.

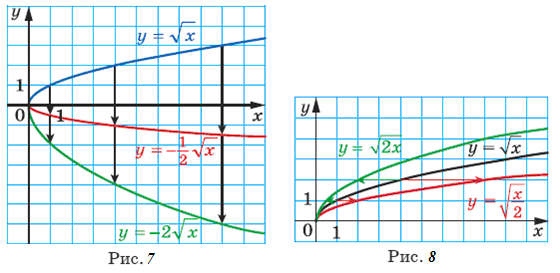
На рисунку 9 показано, як за допомогою графіка функції побудовано графік функції

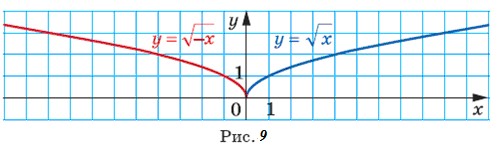
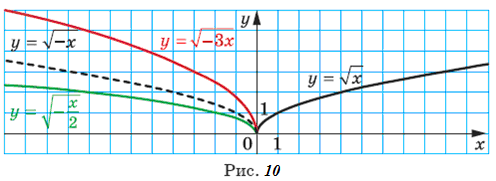
Наприклад, на рисунку 10 показано, як можна за допомогою графіка функції побудувати графіки функцій і

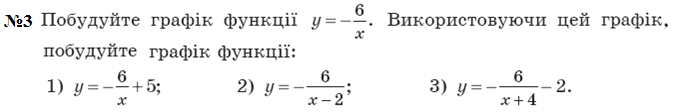
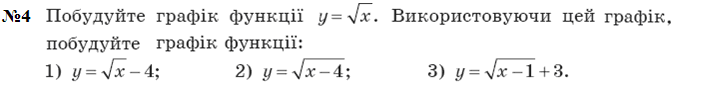
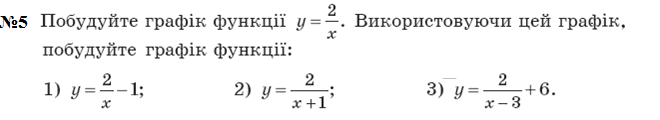
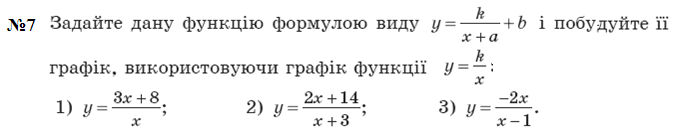
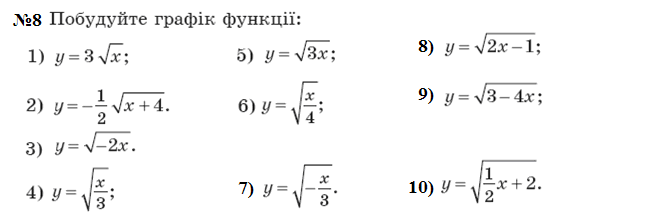
VІ Домашнє завдання.