
- •Урок № 1
- •Хід уроку
- •Повторення шкільного матеріалу
- •Урок № 2
- •Хід уроку
- •V. Викладання матеріалу.
- •Урок № 3
- •Хід уроку
- •Урок № 4
- •Парність та непарність
- •Урок № 6
- •Хід уроку
- •Урок № 7
- •Хід уроку
- •Урок № 8
- •Хід уроку
- •Урок № 9
- •Властивості, що випливають з означення
- •Властивості степеня
- •Властивості арифметичних коренів
- •Урок № 15
- •Урок № 19
- •Хід уроку
- •Урок № 20
- •Урок № 28
- •Хід уроку
- •Урок № 29
- •Хід уроку
- •Рішення системи лінійних рівнянь методом підстановки
- •Рішення системи методом почленного складання (вирахування) рівнянь системи
- •Поняття визначника
- •Теорема (правило Крамера).
- •Урок № 30
- •Хід уроку
- •Урок № 31
- •Хід уроку
- •Метод інтервалів
- •Урок № 32
- •Використана література
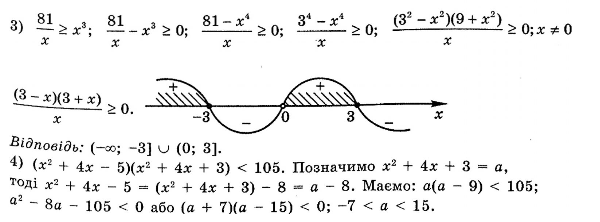
Метод інтервалів
Отже,
нехай функція
![]() неперервна
на інтервалі І
й перетворюється на 0 у скінченній
кількості точок цього інтервалу. Тоді
інтервал І
розбивається цими точками на інтервали,
в кожному з яких
неперервна
на інтервалі І
й перетворюється на 0 у скінченній
кількості точок цього інтервалу. Тоді
інтервал І
розбивається цими точками на інтервали,
в кожному з яких
![]() зберігає
незмінний знак. Щоб визначити цей знак,
достатньо обчислити значення
зберігає
незмінний знак. Щоб визначити цей знак,
достатньо обчислити значення![]() у
будь-якій точці кожного такого інтервалу.
у
будь-якій точці кожного такого інтервалу.
Приклад
Розв’язати
нерівність
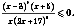
Розглянемо функцію
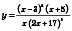 .
.
![]() (див.
рисунок):
(див.
рисунок):
![]() Знайдемо
нулі функції
Знайдемо
нулі функції
![]() :
:
![]() ,
,
![]() .
.
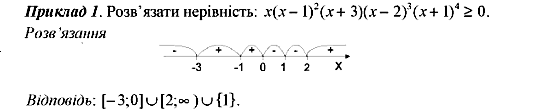
Ці точки поділяють область визначення функції на інтервали, в кожному з яких функція зберігає постійний знак (див. рисунок):
![]()
![]() .
.
Отже, для
![]() отримали
отримали![]() (ставимо
на рисунку знак «+» над цим інтервалом).
(ставимо
на рисунку знак «+» над цим інтервалом).
Зверніть увагу:
в умові
![]() показник
степеня — парне число. Це означає, що
знаки
показник
степеня — парне число. Це означає, що
знаки![]() по
різні боки від числа 3 однакові.
по
різні боки від числа 3 однакові.
Решта показників степеня — числа непарні. Тому, переходячи через точки 0; -5; -8,5, знаки змінюємо на протилежні.
Обираємо проміжки,
над якими стоїть знак «-». Нерівність
нестрога, тому число -5 теж є
розв’язком.
Відповідь:
![]() .
.



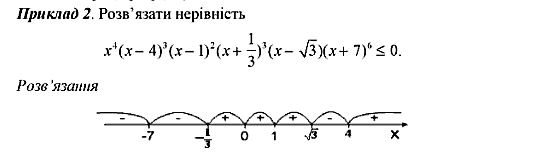


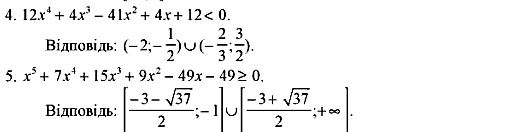
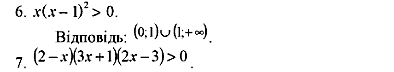

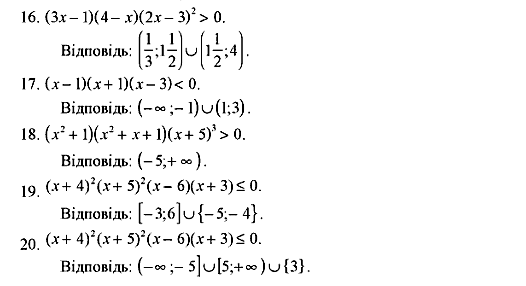
Урок № 32
Тема: Розв׳язування показниково-логарифмічних нерівностей.
Мета: Закріпити знання студентів щодо розв׳язування показниково-логарифмічних нерівностей
Поняття та терміни:. показниково-логарифмічні нерівності
Обладнання: дошка, роздатковий матеріал.
Тип уроку:комбінований.
Хід уроку
І. Організаційний момент. (5 хв)
ІІ. Перевірка домашнього завдання. (15 хв)
ІІІ Повідомлення теми, формулювання мети і основних завдань (5 хв)
ІV. Викладання матеріалу.(53 хв)
V. Домашнє завдання (2 хв)
ІV. Викладання матеріалу.
Правило 1

Правило 2

1. Розв’яжіть нерівність
1.
![]()
2.
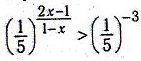
3.
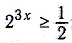
4.
![]()
2.
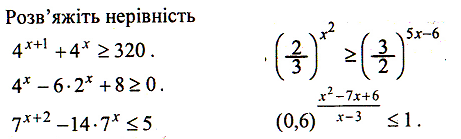
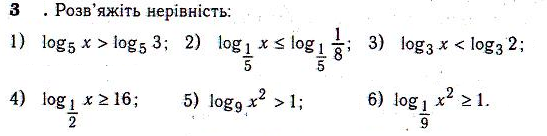
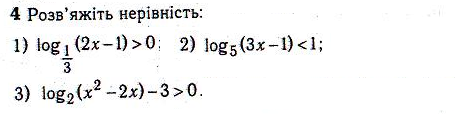
4)![]() 5)
5)![]()
6)
![]() 7)
7)![]()
![]()
![]()
![]()
![]()
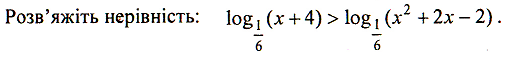
![]()
![]()
Урок № 33
Тема: Рівносильні перетворення нерівностей та загальний метод інтервалів.
Мета: Закріпити знання студентів щодо розв’язування нерівностей методом інтервалів
Поняття та терміни:. Загальний метод інтервалів
Обладнання: дошка, роздатковий матеріал.
Тип уроку:комбінований.
Хід уроку
І. Організаційний момент. (5 хв)
ІІ. Перевірка домашнього завдання. (15 хв)
ІІІ Повідомлення теми, формулювання мети і основних завдань (5 хв)
ІV. Викладання матеріалу.(53 хв)
V. Домашнє завдання (2 хв)
ІV. Викладання матеріалу.


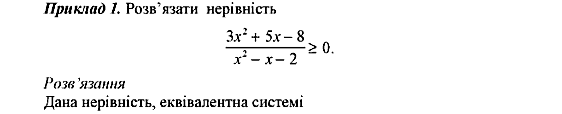
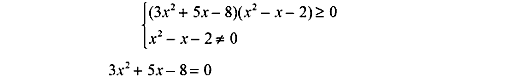




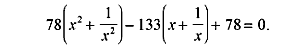
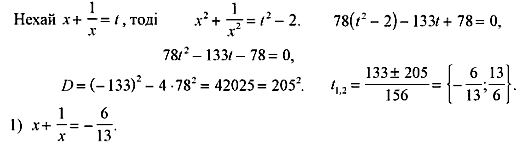
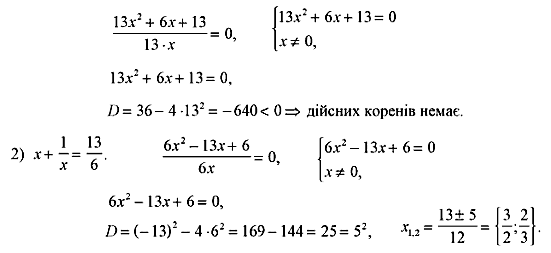



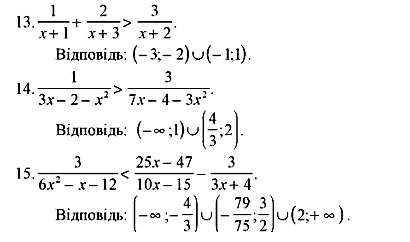

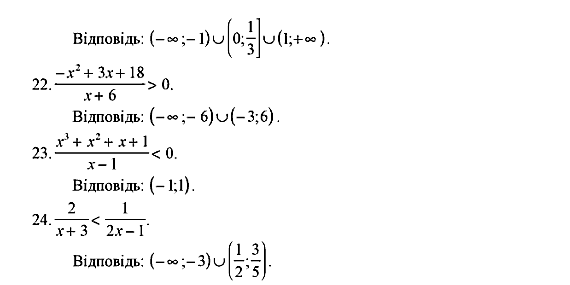
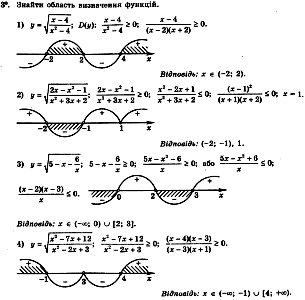
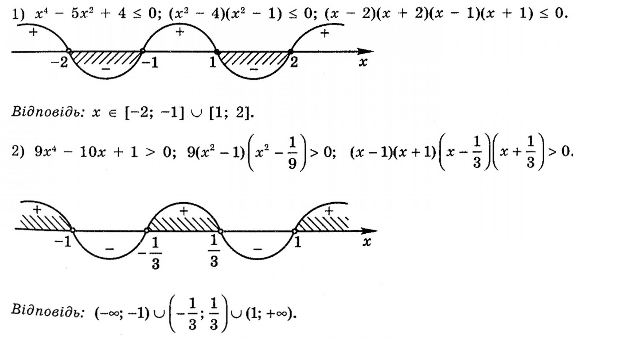
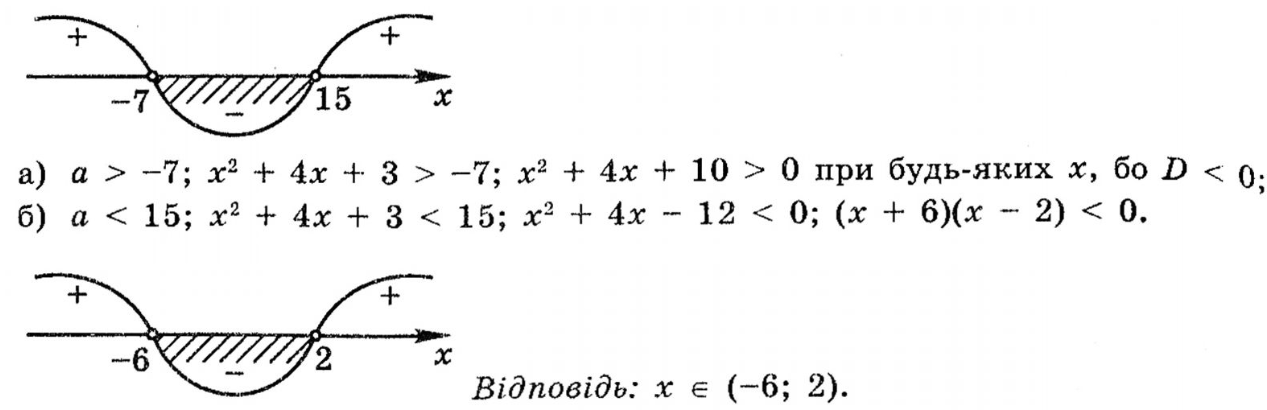
Урок № 34
Тема: Рівняння і нерівності з модулем.
Мета: Закріпити знання студентів щодо розв׳язування рівнянь та нерівностей з модулем
Поняття та терміни:. показниково-логарифмічні нерівності
Обладнання: дошка, роздатковий матеріал.
Тип уроку:комбінований.
Хід уроку
І. Організаційний момент. (5 хв)
ІІ. Перевірка домашнього завдання. (15 хв)
ІІІ Повідомлення теми, формулювання мети і основних завдань (5 хв)
ІV. Викладання матеріалу.(53 хв)
V. Домашнє завдання (2 хв)
ІV. Викладання матеріалу.
Приклад 1.
![]()
Відповідь:
Приклад 2.
Визначити
суму розв’язків рівняння
![]()
Розв’язання
. Відкриємо модуль у лівій частині рівняння. Отримаємо два випадки:
1)
![]()
![]()
2)
![]()
![]()
Отже,
сума розв’язків рівняння дорівнює
![]()
Відповідь: -14.
Приклад 3.
Визначити
розв’язок рівняння
![]() у
проміжку
у
проміжку![]()
Розв’язання
Для
значень
![]() з
проміжку
з
проміжку![]() маємо
маємо![]() і
і![]() Отже,
при
Отже,
при![]() рівняння
матиме вигляд
рівняння
матиме вигляд![]() Звідси
Звідси![]() і
і![]()
Відповідь: 2,7.
Приклад 4.
Обчислити
суму цілих розв’язків рівняння
![]()
Розв’язання.
Запишемо
![]()
Розглянемо випадки:
1)
![]() тоді
тоді![]()
![]()
![]()
2)
![]() тоді
тоді![]()
![]()
![]() отже,
усі значення
отже,
усі значення
![]() з
проміжку
з
проміжку![]() задовольняють
рівняння.
задовольняють
рівняння.
3)
![]() тоді
тоді![]()
![]()
![]()
Цілі
числа
![]() є
розв’язками рівняння. Їхня сума дорівнює
є
розв’язками рівняння. Їхня сума дорівнює![]()
Відповідь: 9.
Приклад 5.
![]()
Приклад 6.
|x+3|-|x-3|=2
|x+5|+|x-7|=4
|x-2 |-|x+9|=-2
\x-3|+|x+11|=7
|x+7|-|x-7|=3
|x+2|+|x-10|=12
|x+6|-|x+8|=-4
|3+x|-|x-7|=11
|x-9|-|5+x|=8
|x-1|+|12+x|=15
|x-2|-|x+7|=10
|4+x|+|x-2|=6
|x+8|-|x-11|=14
|x-4|+|x-8|=-1
|x+2|+|x-10|=6
|x-12|-|x+10|=2

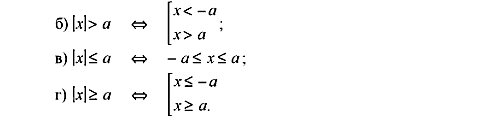


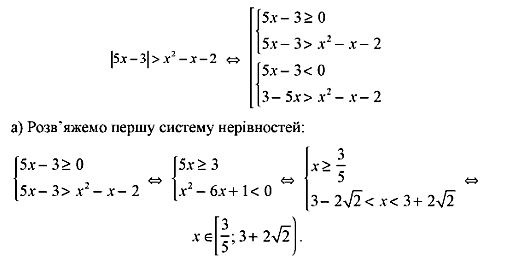





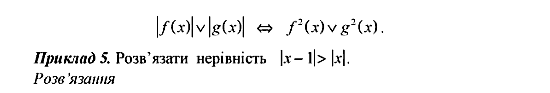




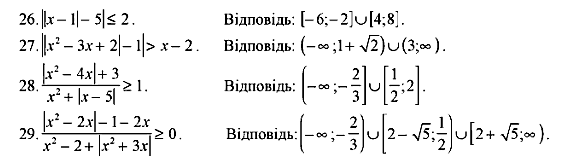
VІ Домашнє завдання.
1)
![]()
2)
![]()
3)
Обчислити суму цілих розв’язків
рівняння
![]()
