Занятие 5. Непрерывная случайная величина.
Задача 1.
Непрерывная случайная величина задана интегральной функцией распределения
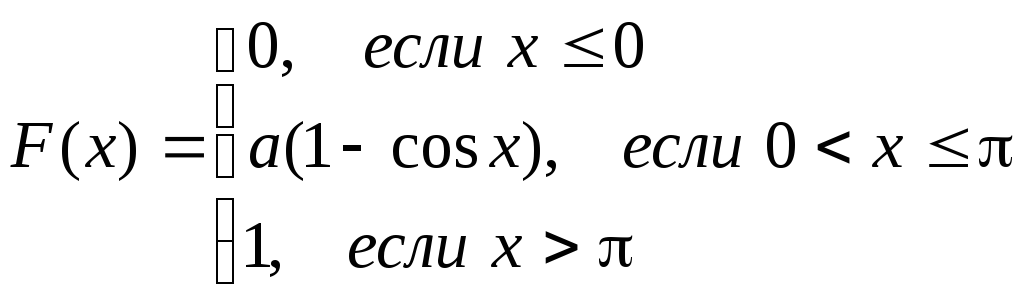
Определить:
,
значение параметраa,
вероятность
,
построить графики функций
.
Решение.
Функция
плотности
,
следовательно:
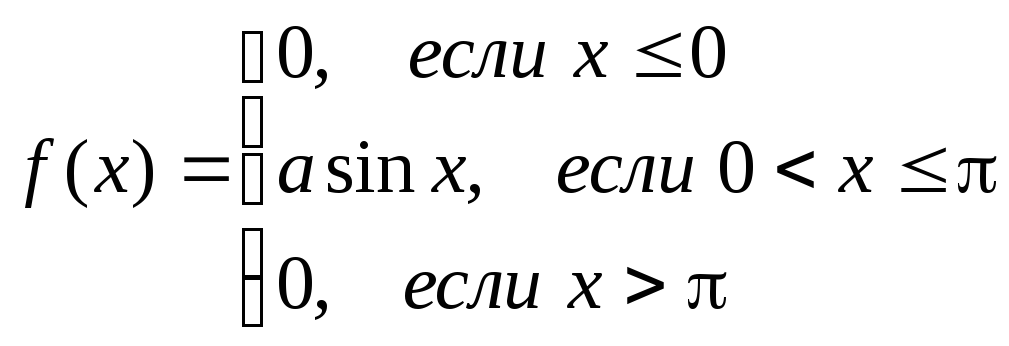
Для
определения значения параметра a
воспользуемся
свойством
.
Таким образом, интегральная функция распределения имеет вид:
Функция плотности имеет вид:
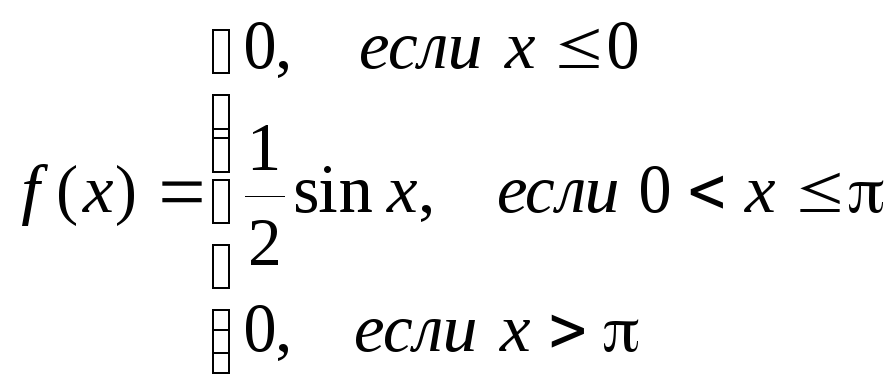
Вероятность
попадания случайной величины на заданный
отрезок [a,
b]
определяетсяпо формуле:
или
.
График функции плотности f(x):
График интегральной функции распределения F(x):
Задача 2.
Непрерывная случайная величина задана плотностью распределения:
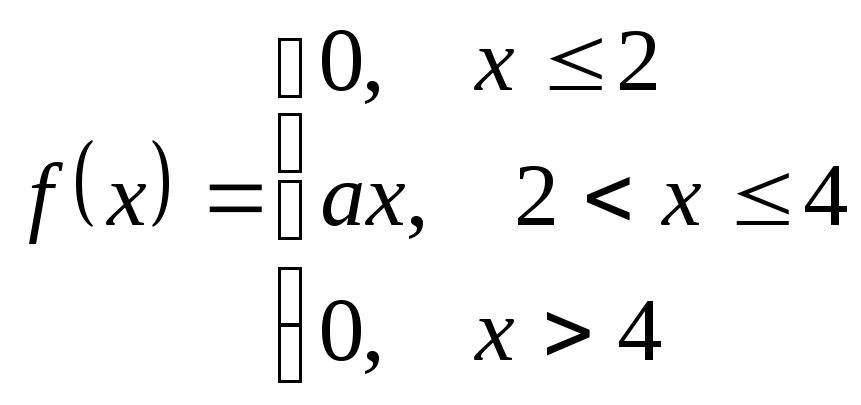
Определить значение параметра a, интегральную функцию распределения F(x), значения mx, Dx, σx, построить графики функций f(x) и F(x).
Решение.
Для
определения значения параметра a
воспользуемся
свойством
.
Функция плотности имеет вид:
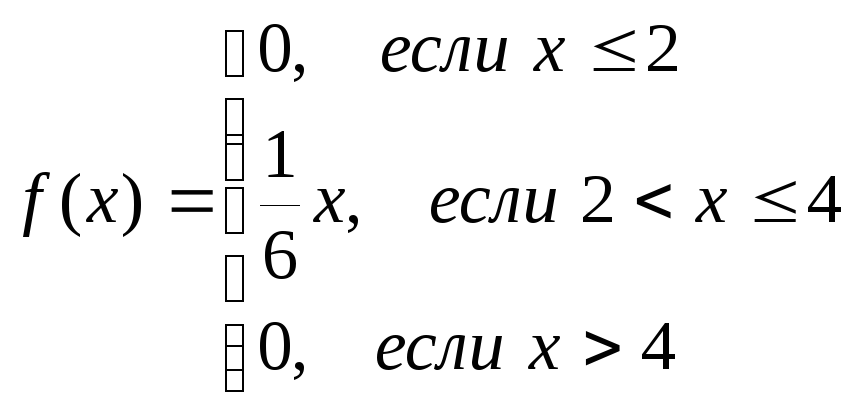
Интегральная функция распределения F(x) определяется по формуле:
1)
2)
3)
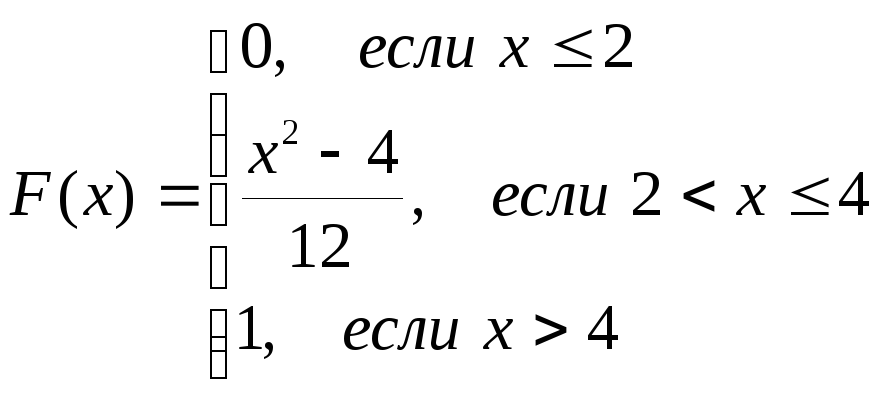
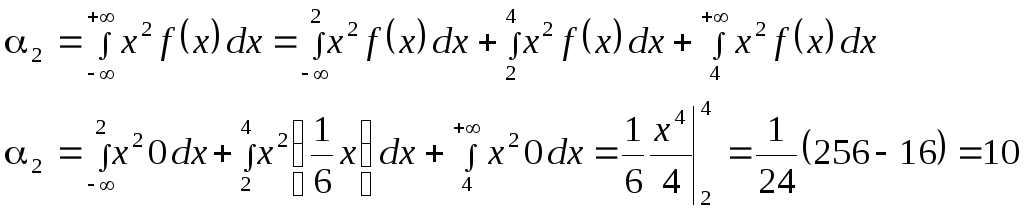
График функции плотности f(x):
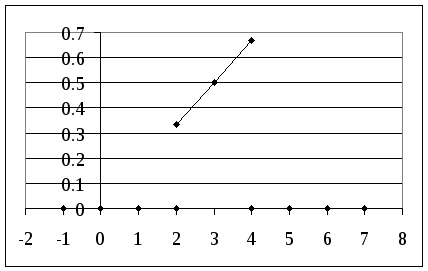
График интегральной функции распределения F(x):
Контрольные вопросы:
Определение непрерывной случайной величины.
Определение закона распределения случайной величины.
Интегральная функция распределения случайной величины. Определение и свойства.
Плотность распределения вероятности. Определение и свойства.
Вероятность попадания непрерывной случайной величины в заданный интервал.
Определение функции распределения по известной плотности распределения.
Характеристики положения случайной величины на числовой оси (математическое ожидание, мода, медиана).
Начальные и центральные моменты случайных величин. Свойства моментов случайных величин.
Равномерный закон распределения случайной величины (дифференциальная и интегральная функции распределения и их графики; числовые характеристики; вероятность попадания случайной величины на заданный участок).
Показательный закон распределения (дифференциальная и интегральная функции распределения и их графики; числовые характеристики; вероятность попадания случайной величины на заданный участок).
Нормальный закон распределения (дифференциальная и интегральная функции распределения и их графики; числовые характеристики; вероятность попадания случайной величины на заданный участок).
Занятие 6.
Определение законов распределения случайных величин на основе опытных данных.
Задача.
Для заданной выборки значений случайной величины:
Построить статистический ряд распределения.
Построить гистограмму.
Выдвинуть гипотезу о законе распределения случайной величины.
Алгоритм решения задачи.
Построение статистического ряда распределения.
Найти среди элементов выборки минимальный (xmin) и максимальный (xmam).
Определить длину интервалов Δ (рекомендуемая точность вычисления 0,001)
Определить границы интервалов разбиения
Определить числа попадания значений случайной величины в i-ый интервал mi. (В случае попадания значения случайной величины на границу двух интервалов, следует относить его к каждому интервалу со значением 0,5)
Определить частоту попадания случайной величины i-ый интервал
pi*=mi/n n=120
Результаты оформить в виде таблицы.
Построение гистограммы.
Определить значение ординаты i-ого интервала
.
Результаты добавить в таблицу.Построить график гистограммы. Для построения графика гистограммы откладывают по оси абсцисс интервалы, на каждом из которых строят прямоугольник, площадь которого равна частоте pi*. высота прямоугольника равна hi.
3. По виду гистограммы визуально определяем вид теоретического распределения, к которому ближе всего подходит исследуемое распределение.
Примеры решения задачи.
Вариант А.
Исходные данные:
|
4.8467 |
12.9628 |
9.3495 |
16.4017 |
9.0761 |
16.5549 |
7.0532 |
7.6100 |
|
7.9379 |
3.3204 |
2.9131 |
13.7651 |
14.1493 |
5.4408 |
3.7188 |
3.2660 |
|
9.0316 |
5.0934 |
13.1611 |
8.8034 |
6.2457 |
17.3561 |
17.4386 |
9.1817 |
|
5.5954 |
15.7492 |
18.3164 |
2.9781 |
14.0546 |
8.9109 |
14.8116 |
11.0091 |
|
9.7844 |
14.3664 |
9.6883 |
3.4857 |
5.4967 |
12.2179 |
12.2765 |
13.9716 |
|
12.2953 |
2.9978 |
11.1385 |
2.9056 |
5.9705 |
15.7652 |
11.5515 |
15.2869 |
|
13.3486 |
16.5690 |
15.2977 |
4.2808 |
5.5114 |
9.0305 |
10.7604 |
6.4758 |
|
17.6075 |
14.8104 |
15.8264 |
7.4771 |
11.9982 |
14.9045 |
6.6351 |
10.4492 |
|
11.1525 |
9.8217 |
4.6938 |
17.8907 |
13.4044 |
7.6967 |
8.2409 |
15.1920 |
|
14.1967 |
12.8126 |
7.7323 |
13.5751 |
14.2777 |
6.0178 |
5.7643 |
4.5950 |
|
13.3691 |
5.3586 |
14.1319 |
15.4431 |
7.7789 |
13.3484 |
14.5843 |
4.8413 |
|
9.2909 |
14.2548 |
10.9000 |
18.9062 |
16.5063 |
4.5667 |
13.5597 |
10.9410 |
|
12.2266 |
15.7549 |
8.7716 |
5.1522 |
17.5212 |
19.0202 |
6.1730 |
7.5362 |
|
3.3680 |
12.0995 |
11.9077 |
10.1777 |
13.5423 |
3.2311 |
10.3137 |
7.1981 |
|
6.4126 |
3.2374 |
6.3173 |
16.4537 |
12.0274 |
6.8320 |
13.0451 |
15.5925 |
|
x min |
x max |
i(x max-x min) |
|
2.9056 |
19.0202 |
1.3429 |
|
№ интерв |
xi |
xi+1 |
mi |
pi* |
hi |
fi теор |
|
1 |
2.9056 |
4.2485 |
11 |
0.0917 |
0.0683 |
0.0621 |
|
2 |
4.2485 |
5.5914 |
12 |
0.1000 |
0.0745 |
0.0621 |
|
3 |
5.5914 |
6.9343 |
11 |
0.0917 |
0.0683 |
0.0621 |
|
4 |
6.9343 |
8.2772 |
10 |
0.0833 |
0.0621 |
0.0621 |
|
5 |
8.2772 |
9.6200 |
9 |
0.0750 |
0.0559 |
0.0621 |
|
6 |
9.6200 |
10.9629 |
9 |
0.0750 |
0.0559 |
0.0621 |
|
7 |
10.9629 |
12.3058 |
12 |
0.1000 |
0.0745 |
0.0621 |
|
8 |
12.3058 |
13.6487 |
11 |
0.0917 |
0.0683 |
0.0621 |
|
9 |
13.6487 |
14.9916 |
13 |
0.1083 |
0.0807 |
0.0621 |
|
10 |
14.9916 |
16.3344 |
9 |
0.0750 |
0.0559 |
0.0621 |
|
11 |
16.3344 |
17.6773 |
9 |
0.0750 |
0.0559 |
0.0621 |
|
12 |
17.6773 |
19.0202 |
4 |
0.0333 |
0.0248 |
0.0621 |
|
|
|
|
120 |
1 |
|
|
Выдвигается гипотеза о равномерном законе распределения исследуемой случайной величины.
Вариант В.
Исходные данные:
|
0.5718 |
0.4201 |
0.0054 |
2.4551 |
0.1314 |
1.5684 |
0.5216 |
0.1879 |
|
0.4130 |
0.5402 |
1.9503 |
1.2811 |
0.1957 |
0.7998 |
0.1335 |
0.0082 |
|
1.2281 |
3.1938 |
0.9514 |
0.0082 |
0.1967 |
1.7396 |
2.6439 |
0.9671 |
|
0.1403 |
1.2313 |
0.2690 |
0.1469 |
0.2181 |
0.9203 |
1.7799 |
0.2274 |
|
0.1562 |
1.3141 |
0.9110 |
0.0241 |
3.1630 |
0.4248 |
0.2749 |
0.8385 |
|
0.5489 |
1.1208 |
0.9304 |
0.1770 |
0.8186 |
0.0424 |
0.1160 |
0.0154 |
|
0.4316 |
0.5002 |
0.5212 |
2.9174 |
1.0317 |
0.7882 |
3.4780 |
2.3309 |
|
0.8717 |
0.3496 |
2.5385 |
0.5295 |
0.3284 |
0.5653 |
0.1509 |
0.9061 |
|
0.5127 |
0.0072 |
0.2274 |
1.0646 |
0.2277 |
7.6930 |
0.1261 |
0.1431 |
|
1.4845 |
3.5396 |
2.7041 |
0.4184 |
0.9752 |
0.7858 |
1.2992 |
0.9314 |
|
0.1748 |
1.4368 |
1.9304 |
1.8643 |
2.6358 |
0.6962 |
2.4378 |
0.1051 |
|
1.2127 |
0.4849 |
3.8199 |
0.6695 |
3.8569 |
0.3125 |
0.0432 |
2.4774 |
|
4.8876 |
1.4134 |
1.2387 |
3.0755 |
2.5019 |
0.9097 |
0.3139 |
0.5477 |
|
0.8412 |
0.4366 |
0.5867 |
0.9634 |
0.9505 |
0.9788 |
1.3310 |
0.7883 |
|
0.2675 |
0.3500 |
1.1479 |
0.0953 |
0.3248 |
0.7912 |
1.2008 |
1.4677 |
|
x min |
x max |
i(x max-x min) |
|
0.0054 |
7.6930 |
0.6406 |
|
№ интерв |
xi |
xi+1 |
mi |
pi* |
hi |
fi теор |
|
1 |
0.0054 |
0.6460 |
55 |
0.4583 |
0.7154 |
0.6839 |
|
2 |
0.6460 |
1.2866 |
33 |
0.2750 |
0.4293 |
0.3784 |
|
3 |
1.2866 |
1.9273 |
11 |
0.0917 |
0.1431 |
0.2093 |
|
4 |
1.9273 |
2.5679 |
8 |
0.0667 |
0.1041 |
0.1158 |
|
5 |
2.5679 |
3.2085 |
7 |
0.0583 |
0.0911 |
0.0641 |
|
6 |
3.2085 |
3.8492 |
3 |
0.0250 |
0.0390 |
0.0354 |
|
7 |
3.8492 |
4.4898 |
1 |
0.0083 |
0.0130 |
0.0196 |
|
8 |
4.4898 |
5.1305 |
1 |
0.0083 |
0.0130 |
0.0108 |
|
9 |
5.1305 |
5.7711 |
0 |
0.0000 |
0.0000 |
0.0060 |
|
10 |
5.7711 |
6.4117 |
0 |
0.0000 |
0.0000 |
0.0033 |
|
11 |
6.4117 |
7.0524 |
0 |
0.0000 |
0.0000 |
0.0018 |
|
12 |
7.0524 |
7.6930 |
1 |
0.0083 |
0.0130 |
0.0010 |
|
|
|
|
120 |
1 |
|
|
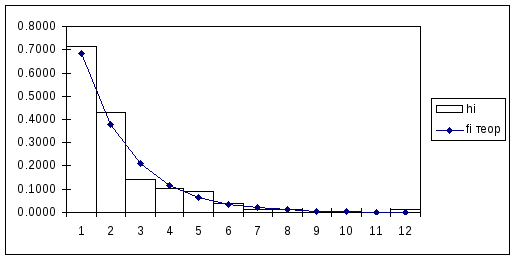
Выдвигается гипотеза о показательном законе распределения исследуемой случайной величины.
Вариант С.
Исходные данные:
|
21.9127 |
33.9000 |
17.8108 |
20.6635 |
28.0139 |
20.4649 |
32.0696 |
32.7042 |
|
47.5807 |
26.8992 |
21.0090 |
32.7729 |
32.3879 |
39.6364 |
27.0290 |
28.7844 |
|
27.3458 |
31.1870 |
13.5304 |
9.4052 |
25.6430 |
25.0631 |
26.4673 |
16.8856 |
|
19.2236 |
26.3964 |
23.7193 |
19.1509 |
21.0568 |
17.4472 |
29.3717 |
36.8890 |
|
37.2957 |
22.1205 |
25.4153 |
28.5411 |
25.0545 |
24.4811 |
18.4894 |
30.1899 |
|
16.7999 |
25.2566 |
33.9311 |
19.1669 |
33.5968 |
21.9890 |
29.0924 |
9.7886 |
|
35.1000 |
39.9651 |
27.0621 |
20.4999 |
23.8667 |
31.4315 |
33.8930 |
16.5916 |
|
20.2323 |
18.0676 |
23.5023 |
34.9182 |
17.8181 |
25.2655 |
15.4520 |
19.4361 |
|
24.2995 |
26.4716 |
18.4080 |
25.9534 |
36.1375 |
28.8333 |
22.8759 |
26.3660 |
|
36.9573 |
31.8018 |
28.6831 |
21.4950 |
34.5344 |
28.9821 |
23.4336 |
20.3173 |
|
30.2262 |
13.0123 |
14.2993 |
47.1693 |
26.5753 |
26.8632 |
20.3616 |
32.2115 |
|
32.2176 |
36.7825 |
27.4694 |
28.1868 |
26.7761 |
39.0296 |
22.4707 |
33.9070 |
|
19.6587 |
25.2319 |
12.0670 |
22.2327 |
21.5765 |
10.8404 |
28.4685 |
29.6275 |
|
42.2819 |
5.0627 |
23.4138 |
18.3602 |
19.5600 |
32.0359 |
33.3359 |
23.7446 |
|
39.0005 |
27.8452 |
24.6446 |
28.0512 |
23.8713 |
37.2355 |
28.3752 |
23.7889 |
|
x min |
x max |
i(x max-x min) |
|
5.0627 |
47.5807 |
3.5432 |
|
№ интерв |
x(i) |
x(i+1) |
m(i) |
p*(i) |
h(i) |
f теор |
|
1 |
5.0627 |
8.6059 |
1 |
0.0083 |
0.0024 |
0.0023 |
|
2 |
8.6059 |
12.1491 |
4 |
0.0333 |
0.0094 |
0.0065 |
|
3 |
12.1491 |
15.6922 |
4 |
0.0333 |
0.0094 |
0.0149 |
|
4 |
15.6922 |
19.2354 |
13 |
0.1083 |
0.0306 |
0.0277 |
|
5 |
19.2354 |
22.7785 |
18 |
0.1500 |
0.0423 |
0.0417 |
|
6 |
22.7785 |
26.3217 |
20 |
0.1667 |
0.0470 |
0.0507 |
|
7 |
26.3217 |
29.8649 |
26 |
0.2167 |
0.0612 |
0.0500 |
|
8 |
29.8649 |
33.4080 |
13 |
0.1083 |
0.0306 |
0.0399 |
|
9 |
33.4080 |
36.9512 |
11 |
0.0917 |
0.0259 |
0.0258 |
|
10 |
36.9512 |
40.4943 |
7 |
0.0583 |
0.0165 |
0.0135 |
|
11 |
40.4943 |
44.0375 |
1 |
0.0083 |
0.0024 |
0.0057 |
|
12 |
44.0375 |
47.5807 |
2 |
0.0167 |
0.0047 |
0.0020 |
|
|
|
|
120 |
1 |
|
|
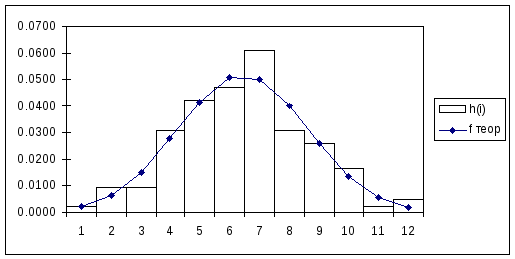
Выдвигается гипотеза о нормальном законе распределения исследуемой случайной величины.
Контрольные вопросы:
Предмет математической статистики и ее основные задачи.
Простая и упорядоченная статистическая совокупность.
Статистическая функция распределения.
Статистический ряд распределения.
Гистограмма.