
- •Занятие 1. Основные понятия теории вероятностей. Классическое определение вероятности. Элементы комбинаторики. Непосредственный подсчет вероятности.
- •Занятие 2. Алгебра событий. Теоремы сложения и умножения. Модели надежности технических систем.
- •Занятие 3
- •Занятие 4. Дискретная случайная величина.
- •Занятие 5. Непрерывная случайная величина.
- •Определение законов распределения случайных величин на основе опытных данных.
- •Занятие 7. Определение числовых характеристик статистического распределения. Сглаживание статистических рядов.
- •Занятие 8. Проверка статистических гипотез.
- •Критические точки распределения χ2.
Занятие 2. Алгебра событий. Теоремы сложения и умножения. Модели надежности технических систем.
Задача №1.
Брошена кость. Определить вероятность выпадения четного числа очков.
Решение.
Обозначим события::
А– выпадение четного числа очков;
А1–выпадение двух очков;
А2–выпадение четырех очков;
А3–выпадение шести очков.
А=А1+А2+А3
А1,А2,А3– события несовместные, следовательно,
P(A)=P(A1)+P(A2)+P(A3)
P(A1)=P(A2)=P(A3)=1/6
P(A)=![]()
Задача №2.
Брошена кость и монета. Определить вероятность выпадения пяти очков на кости и герба на монете.
Решение.
Обозначим события::
А– выпадение пяти очков на кости и герба на монете;
А1–выпадение пяти очков;
А2–выпадение герба.
А=А1А2
А1и А2– события независимые, следовательно,
P(A)=P(A1)P(A2)
P(A1)=1/6
P(A2=1/2
P(A)=![]()
Задача №3.
Вероятность попадания в цель первого орудия равна 0.7, второго – 0.8. Найти вероятность поражения цели при залпе из двух орудий.
Решение.
Обозначим события::
А– поражение цели;
А1–попадание первого орудия; P(A1)=0.7
А2–попадание второго орудия;P(A2 =0.8
1-ый способ.
А=А1+А2
А1и А2– события совместные, следовательно,
P(A)=P(A1)+P(A2)-P(A1A2)
А1и А2– события независимые, следовательно,
P(A1A2)=P(A1)P(A2)
P(A)=0.7+0.8-0.7.0.8
P(A)=0.94
2-ой способ.
Дополнительно обозначим:
Ā1 – промах первого орудия; Ā2 – промах второго орудия.
А1 иĀ1 – события противоположные, так как они несовместные и образуют полную группу. Поэтому
Р(Ā1)=1–Р(А1); Р(Ā1)=1–0.7=0.3
Аналогично
Р(Ā2)=1–Р(А2); Р(Ā2)=1–0.8=0.2
Представим событие А как сумму трех несовместных событий:
А=А1А2+А1Ā2+Ā1А2
Тогда
P(A)=P(A1А2)+P(А1Ā2)+P(Ā1A2)
А1, А2, Ā1, Ā2– события независимые, следовательно:
P(A1A2)=P(A1)P(A2)=0.7.0.8=0.56
P(А1Ā2)=P(A1)P(Ā2)=0.7.0.2=0.14
P(Ā1A2)=P(Ā1)P(A2)=0.3.0.8=0.24
P(A)=0.56+0.14+0.16=0.94
3-ий способ.
Дополнительно обозначим:
Ā– поражения цели не было.
A и Ā– события противоположные.
Р(А)=1–Р(Ā)
Ā=Ā1Ā2
Ā1, Ā2– события независимые, следовательно:
Р(Ā)=P(Ā1)P(Ā2)=0.3.0.2=0.06
Р(А)=1–0.06=0.94
Задача №4
Студент пришел на экзамен, зная 20 вопросов из 30. Определить вероятность того, что он знает предложенные ему три вопроса.
Решение.
Обозначим события::
А– студент знает предложенные ему три вопроса
А1– знает первый вопрос;
А2– знает второй вопрос;
А3– знает третий вопрос;
А=А1А2А3
События А1,А2,А3 зависимые, так как вероятность того, что студент будет знать ответ на очередной вопрос зависит от того, знал ли он ответы на предыдущие вопросы.
P(А1)=![]()
P(А2/А1)=![]() P(А2/Ā1)=
P(А2/Ā1)=![]()
(Ā1–студент не знает ответ на первый вопрос)
Р(А)=P(A1A2A3)=P(A1)P(A2/A1)P(A3/A1A2)
P(A3/A1A2)=![]()
Р(А)=![]() =0.28
=0.28
Задача №5
Определить надежность системы по заданной надежности ее элементов.
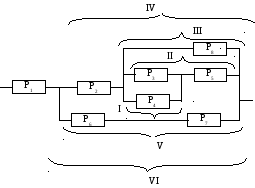
P –надежность
всей системы.
–надежность
всей системы.
P=P1PVI
PVI=1-(1-PIV)(1-PV)
PV=P6P7
PIV=P2PIII
PIII=1-(1-P8)(1-PII)
PII=PIP5
PI=1-(1-P3)(1-P4)
Контрольные вопросы:
Сумма двух событий.
Произведение двух событий.
Сумма нескольких событий.
Произведение нескольких событий.
Теорема о вероятности суммы двух событий.
Условная вероятность событий.
Теорема о вероятности произведения двух событий.
Вероятность произведения нескольких событий.
Противоположные события.
Вероятность суммы противоположных событий.
Определение независимости двух событий.
Определение независимости нескольких событий.
Вероятность произведения независимых событий.
Определение надежности технической системы.
Надежность системы с последовательным соединением элементов.
Надежность системы с параллельным соединением элементов.
