7. Зв’язок між розв’язками неоднорідної й зведеної однорідної системи лінійних рівнянь

Нехай дано довільну систему лінійних неоднорідних рівнянь

(28)

Замінимо в цій системі все вільні члени на нулі, дістанемо систему лінійних однорідних рівнянь

(29)

яку називають зведеною однорідною системою для системи (28). Запишемо системи (28) і (29) у векторній формі

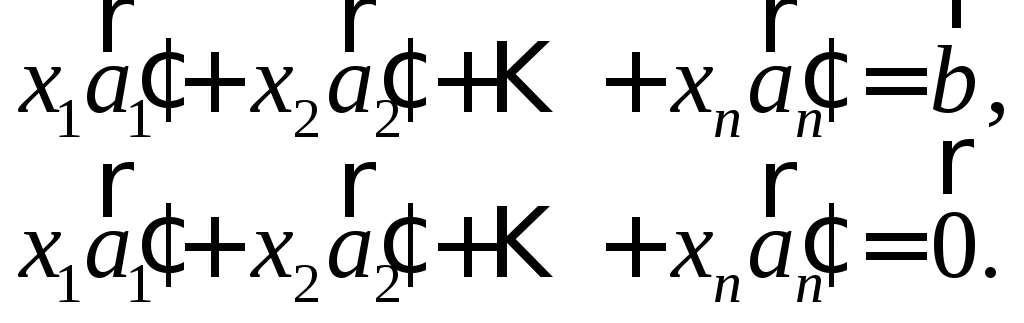
Припустимо, що система (28) сумісна. Тоді справедливі такі твердження.

Теорема 9. Сума будь-якого розв’язку неоднорідної системи (28) і будь-якого розв’язку однорідної системи (29) є розв’язком неоднорідної системи (28).

Нехай і – довільні розв’язки відповідно систем (28) і (29). Тоді

і, отже, вектор є розв’язком системи (28).

Теорема 10. Різниця будь-яких двох розв’язків неоднорідної системи (28) є розв’язком зведеної однорідної системи (29).

Нехай і – довільні розв’язки неоднорідної системи (28). Тоді

і, отже, вектор є розв’язком однорідної системи (29).

Наслідок. Загальний розв’язок неоднорідної системи (28) дорівнює сумі будь-якого розв’язку цієї системи і загального розв’язку зведеної однорідної системи (29).

Нехай – деякий частинний розв’язок системи (28) і – формула, що задає множину всіх розв’язків системи (29).

Тоді є формула, що задає множину всіх розв’язків системи (28).

Вправи для самостійного розв’язування

1. Розв’язати системи лінійних рівнянь методом послідовного виключення невідомих

1) 2)

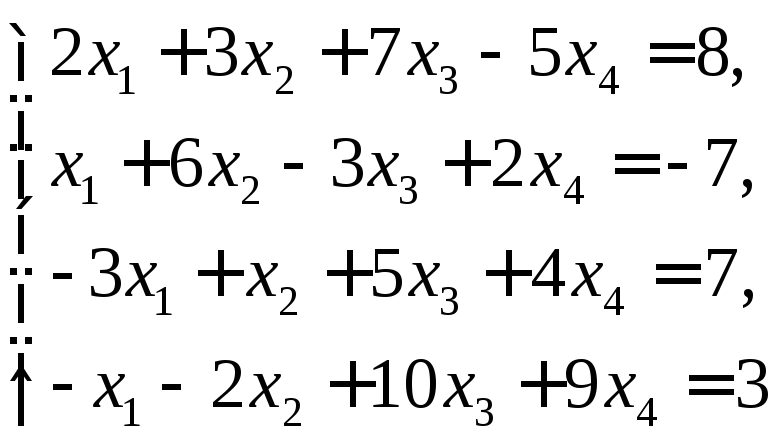
2. Дослідити на сумісність і визначеність систему лінійних рівнянь:

1) 2)

3. Дослідити систему лінійних рівнянь і знайти загальний розв’язок залежно від :

1) 2)

4. Знайти загальний розв’язок і фундаментальну систему розв’язків системи рівнянь:

1) 2)

5. Знайти загальний розв’язок системи лінійних рівнянь, якщо є одним із частинних розв’язків, а вектори і утворюють фундаментальну систему розв’язків для відповідної однорідної системи.

6. Знайти загальний та один частинний розв’язки системи рівнянь:

1) 2)

7. Розв’язати систему лінійних рівнянь матричним методом:

1) 2)

8. Розв’язування систем лінійних рівнянь матричним методом

Розглянемо систему лінійних рівнянь

(30)

яку, як відомо, можна записати у вигляді одного матричного рівняння (§5, п.3)

(31)

де А – матриця системи (30) розміру , і і – вимірні вектори-стовпці. Нехай число рівнянь у системі (30) дорівнює числу невідомих , при чому визначник цієї системи відмінних від нуля. В такому разі у матричному рівнянні (31) – невироджена матриця -го порядку. Припустимо, що матричне рівняння (31) має розв’язок , тобто справджується рівність . Помножимо зліва обидві частини цієї рівність на матрицю . Дістанемо

. (32)

Проте , тому з рівності (32) випливає, що

. (33)

Отже, якщо матричне рівняння (31) з невиродженою матрицею А має розв’язок, то цей розв’язок задається формулою (33) і тому він єдиний. Доведемо, що є розв’язком рівняння (21). Справді , тобто , і є розв’язком рівняння (31). Таким чином, якщо матриця А матричного рівняння (31) невироджена, то рівняння (31) має єдиний розв’язок .

Приклад. Розв’язати систему лінійних рівнянь

Матриця цієї системи

– невироджена, причому

.

Отже, система має єдиний розв’язок

.

Виконуючи множення, знаходимо , тобто .