систему, еквівалентну системі (2). У першому рівнянні цієї системи коефіцієнт при невідомому , буде відмінний від нуля. Тому вважатимемо, що в системі (2) . Застосовуючи елементарні перетворення, зведемо систему (2) до ступінчастого вигляду.

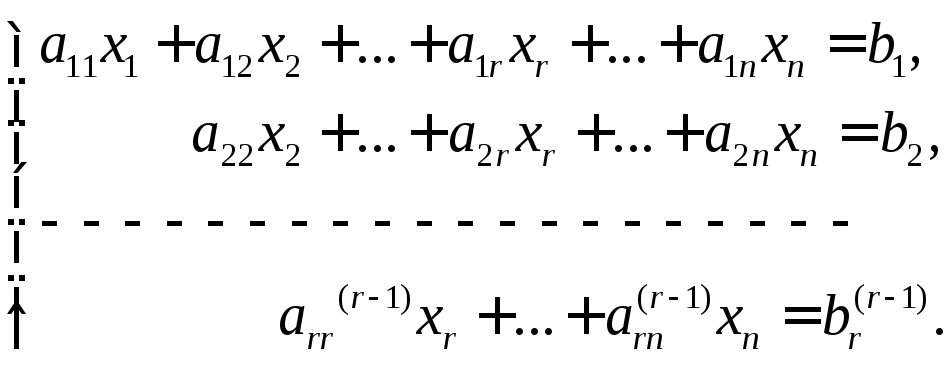(5)

За теоремою 1 ступінчаста система еквівалентна системі (2). Тому розв’язування системи (2) зводимо до розв’язування ступінчастої системи (5). При цьому можливі такі випадки:

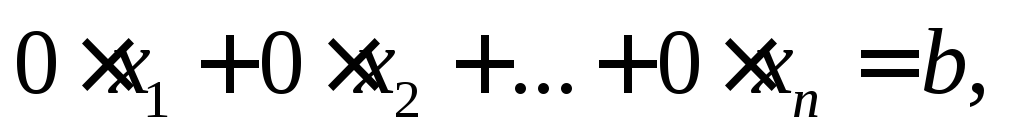
1. В ступінчастій системі (5) міститься рівняння вигляду (скорочено його записують 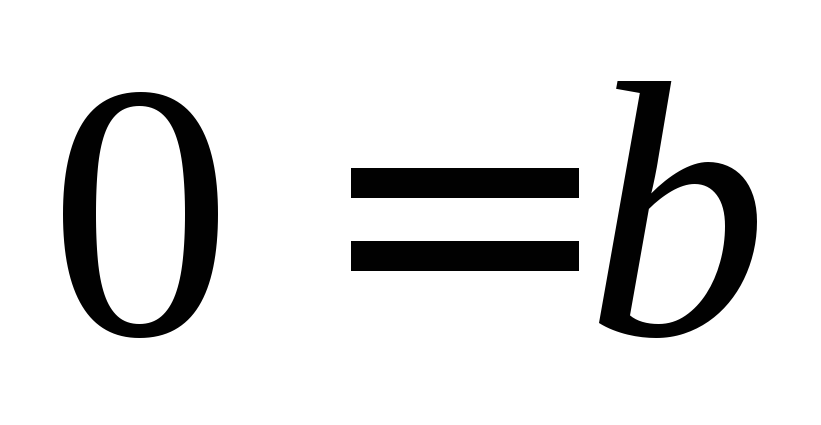). Оскільки жодна система чисел не може задовольнити рівняння 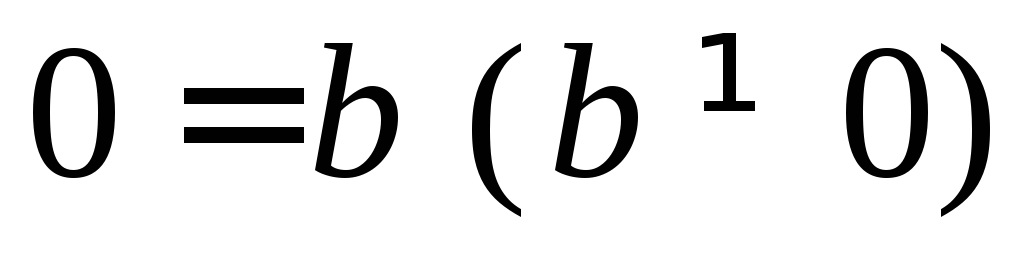, то система рівнянь (5) несумісна.

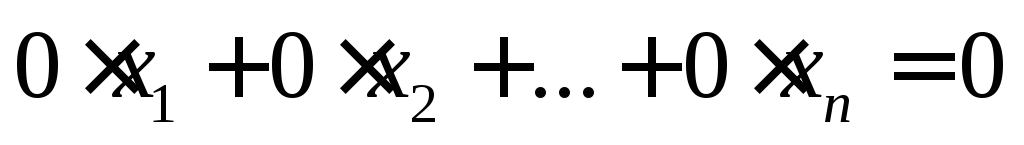2. В системі (5) міститься рівняння вигляду (скорочено ). Довільна сукупність чисел 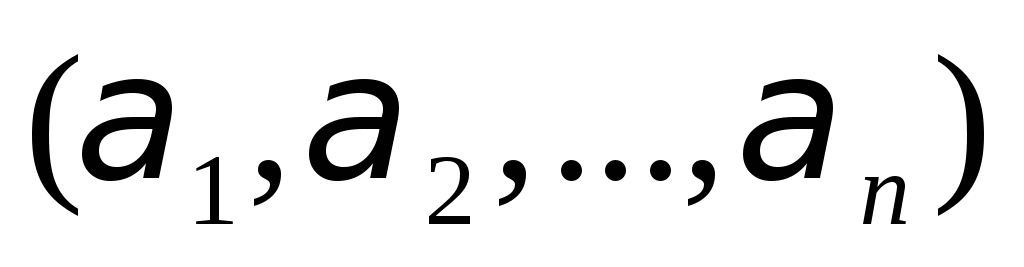є розв’язком цього рівняння, тому його можна відкинути. Дістанемо систему еквівалентну системі (5).

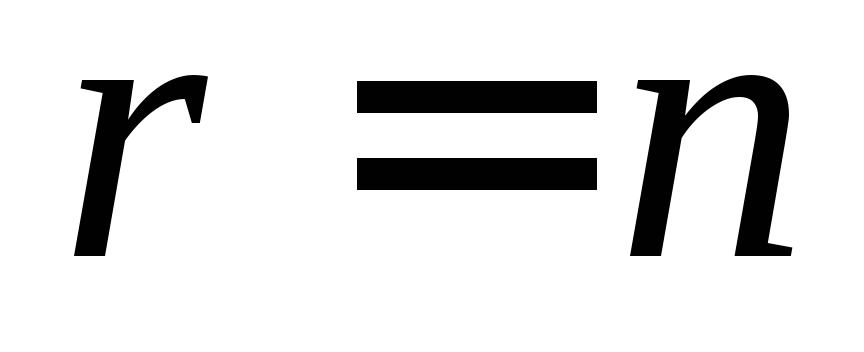3. (число рівнянь 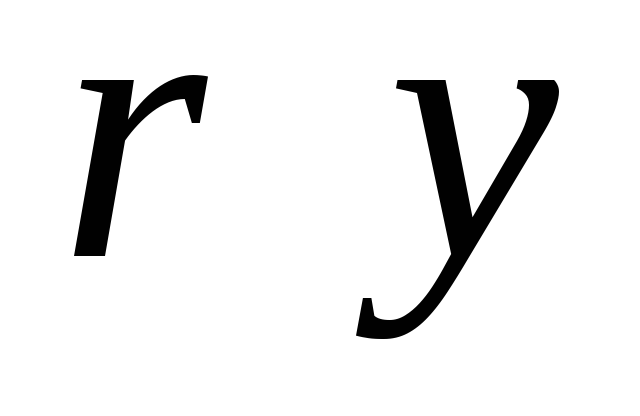ступінчастій системі дорівнює числу невідомих 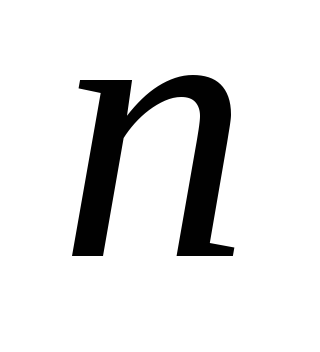). В цьому випадку система (5) моє трикутній вигляд

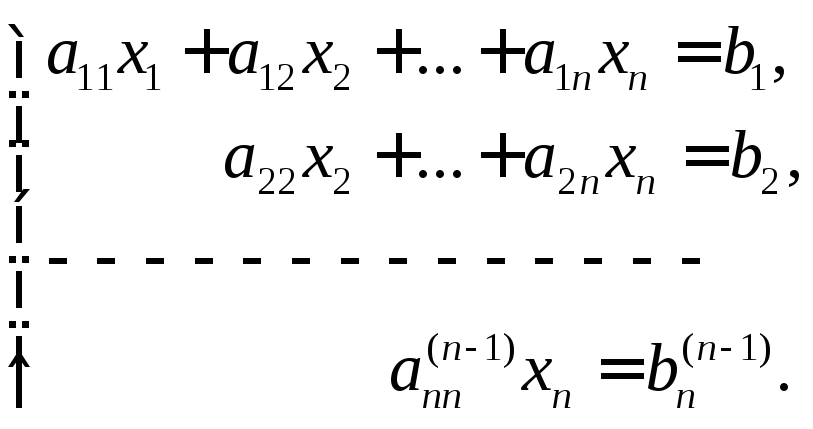(6)

вона сумісна і визначена (моє єдиний розв’язок). З останнього рівняння системи (6) знаходимо невідоме . Підставивши його в передостаннє рівняння системи (6), знайдемо відповідно одне значення невідомого . Тоді таким же способом послідовно дістанемо єдині значення невідомих Добуті таким чином значення невідомих становлять єдиний розв’язок системи (6).

4) (число рівнянь у ступінчастій системі менше числа невідомих ).

Невідомі , з яких починаються перше, друге, ..., -те рівняння системи (5), назвемо головним, а всі інші – вільними. Надамо вільним невідомим довільних значень і знайдемо головні невідомі . Оскільки вільні невідомі можна вибрати довільні, тому множина розв’язків системи (5) у випадку сумісна, але невизначена.

Застосуємо отримані вище результати до однорідної лінійної системи

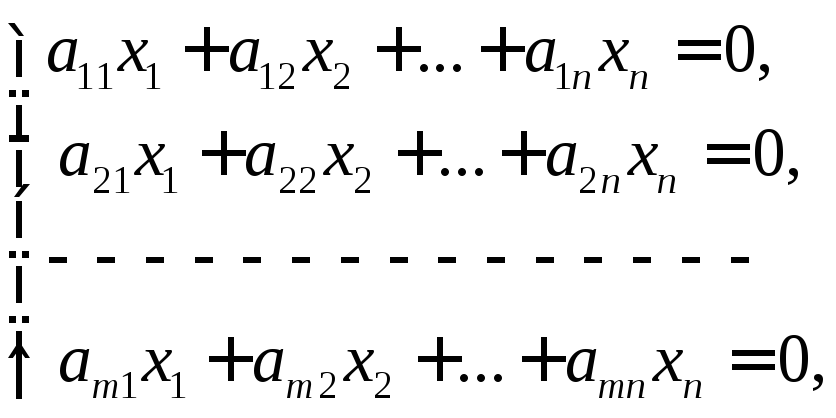(7)

Ця система сумісна, оскільки вона має нульовий розв’язок Справді, оскільки всі вільні члени системи (7) дорівнюють нулю, то вона перетворюється на ступінчасту систему, в якій немає рівняння вигляду .

Якщо система (7) перетворюється на ступінчасту систему, в якій число рівнянь дорівнює числу невідомих , то вона має єдиний розв’язок – нульових. Якщо ж число рівнянь менше, ніж число невідомих , то множина її розв’язків нескінченна, і, отже, вона має ненульові розв’язки. Множина ненульових розв’язків буде нескінченною. Така система невизначена.

Викладений вище метод розв’язування систем лінійних рівнянь називається метод Гауса, або метод послідовного виключення невідомих. Цей метод досить зручний для розв’язування вручну систем лінійних рівнянь з невеликою кількістю невідомих. Він може бути використаний для розв’язування лінійних систем на ЕОМ, проте часто для цього ефективнішим виявляються інші методи, наприклад, ітераційні (послідовних наближень)

Приклади. 1. Розв’язати систему

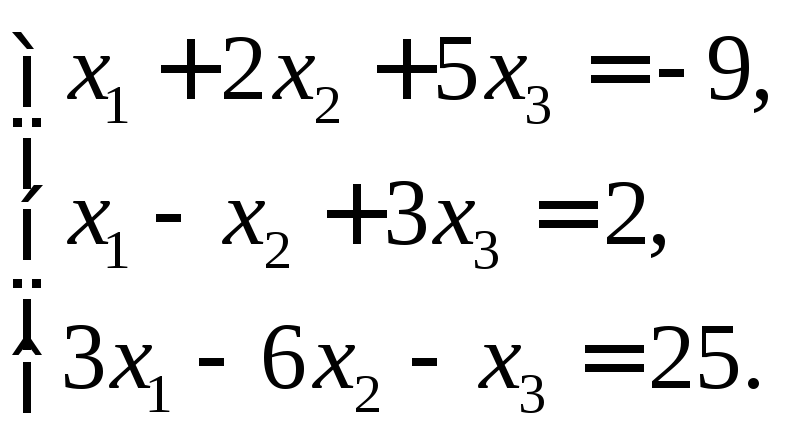
Зведемо розширену матрицю цієї системи до ступінчастого вигляду

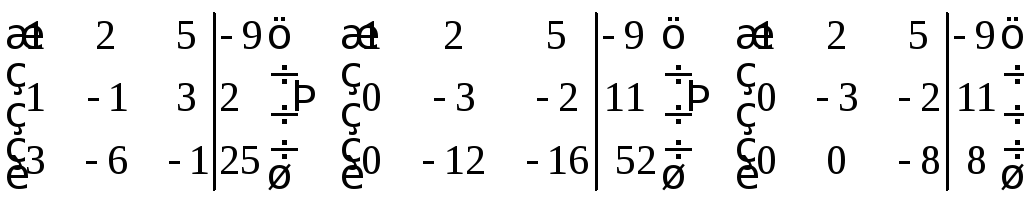
Звідси випливає, що задана система лінійних рівнянь перетвориться на ступінчасту систему

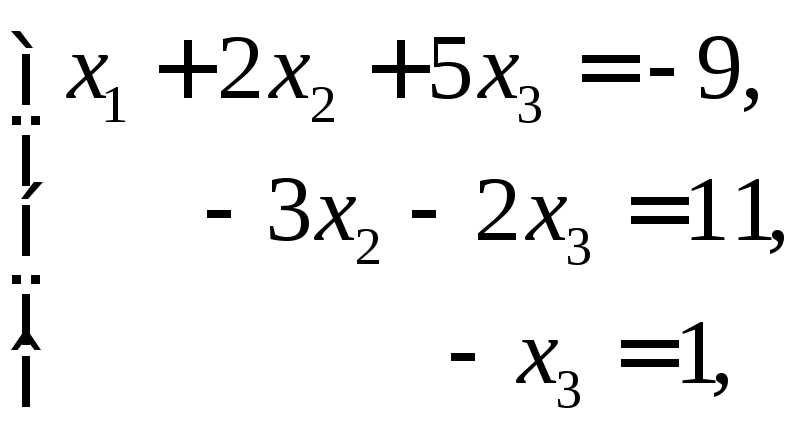
в якій число рівнянь дорівнює числу невідомих. Ця система, а отже, і задана система мають єдиний розв’язок

2. Розв’язати систему

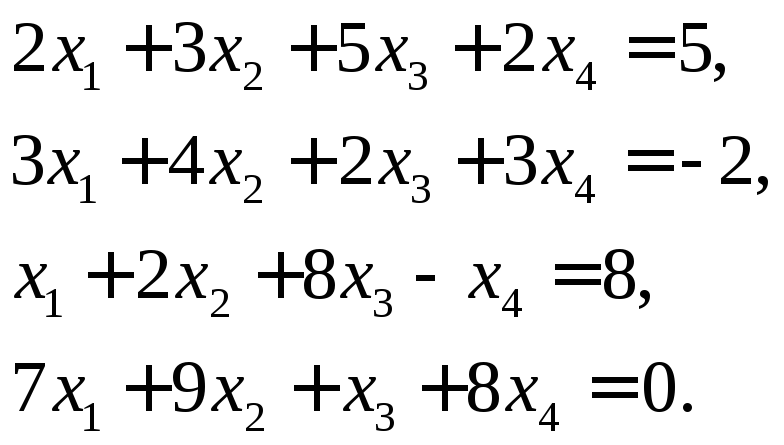
Зведемо розширену матриць до ступінчастого вигляду

Отже, задана система лінійних рівнянь перетворюється на ступінчасту систему, в якій міститься рівняння , тому вона несумісна.

3. Розв’язати систему

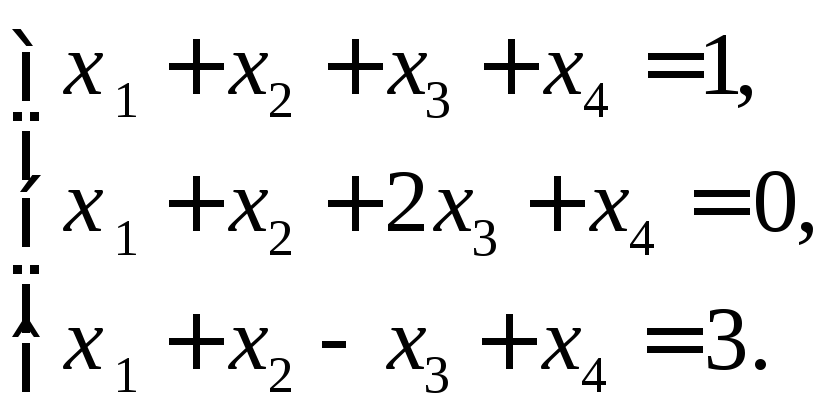
Розширену матрицю цієї системи зведемо до ступінчастого вигляду

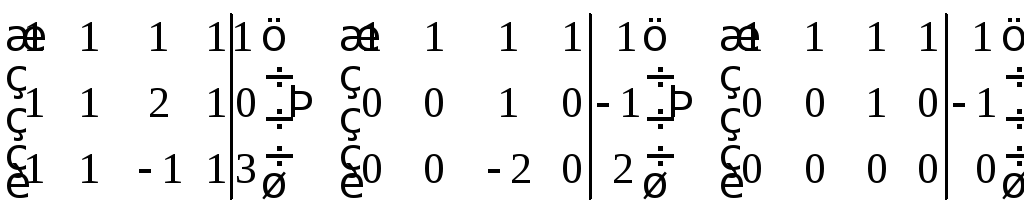
Отже, задана система лінійних рівнянь перетвориться на ступінчасту

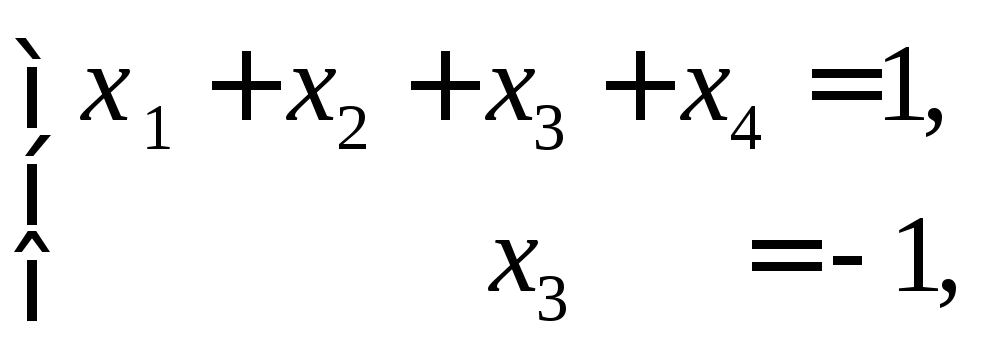
в якій число рівнянь менше числа невідомих. Така система сумісна, але невизначена. Загальний розв’язок запишемо у вигляді – вільні невідомі. Надаючи і довільних значень, будемо мати нескінченну множину розв’язків.

3. Різні форми запису системи лінійних рівнянь

Нехай дано систему лінійних рівнянь

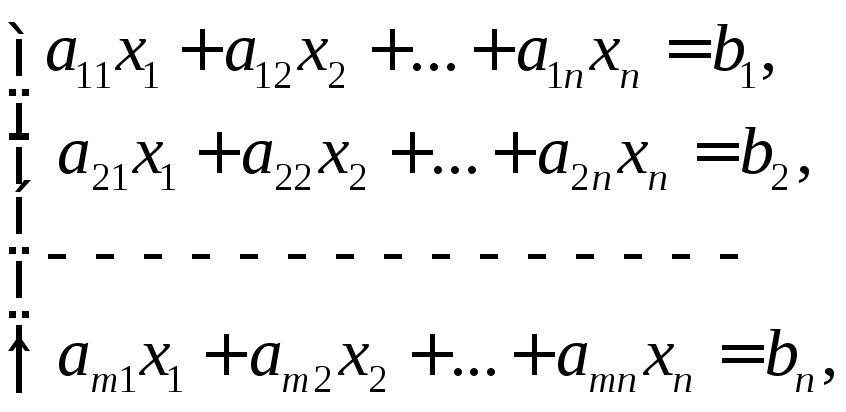(8)

Системі (8) відповідає, складена з коефіцієнтів при невідомих , матриця розміру

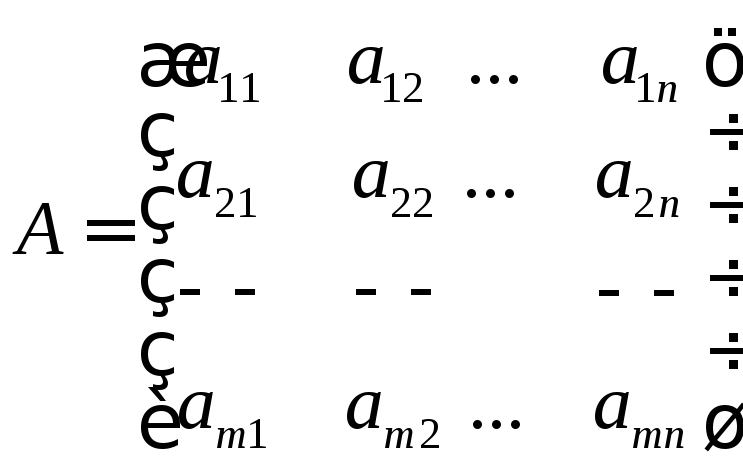
Рядки і стовпці матриці розглядатимемо як вектори. – вектори-рядки.

–вектори-стовпців.

–вектор-стовпець вільних членів.

Загальна система лінійних рівнянь має досить громіздкий вигляд, тому застосовують деякі спрощені її записи. Розглядаючи ліву частину кожного рівняння системи (8), як скалярний добуток вектора-рядка на вектор-стовпця невідомих , дістанемо векторно-скалярний запис системи (8)

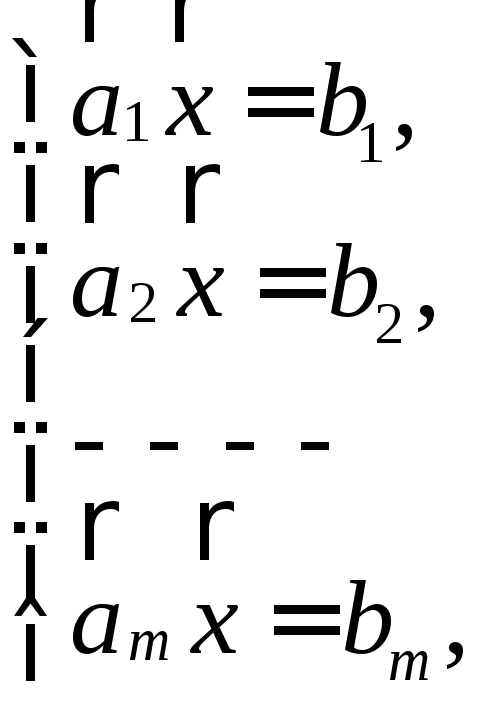або (9)

Систему (8) можна також подати у вигляді

або скорочено матрично-векторна форма запису системи (8).

Ліву частину рівнянь системи (8) розглядатимемо як суму добутків векторів-стовпців на невідомі . Дістанемо векторну форму запису системи (8)

.

У випадку однорідної системи лінійних рівнянь спрощені формули відповідно такі:

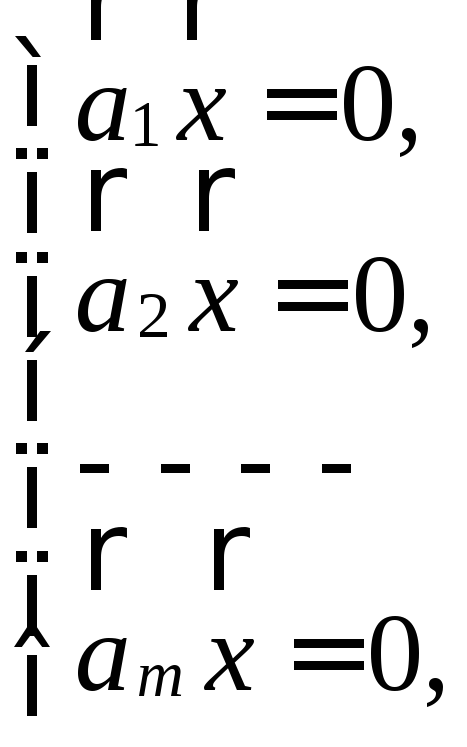або

Однорідна система лінійних рівнянь завжди має нульовий розв’язок який називається тривіальним. А чи має вона ненульові розв’язки? Певну відповідь на це питання дає така теорема.

Теорема 2. Однорідна система лінійних рівнянь з невідомими має ненульовий розв’язок, якщо .

Розглянемо систему

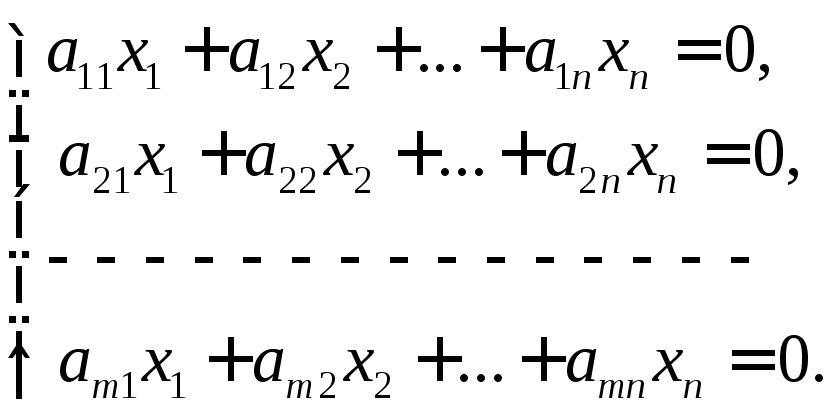(12)

–векторна форма системи (12). Оскільки , то вектори-стовпці лінійно залежні (§3, Теорема 2). Тому існують такі числа які не всі дорівнюють нулю і задовольняють рівність . Тобто числа утворюють ненульовий розв’язок однорідної системи (12).

4. Ранг матриці

Нехай маємо матрицю А розміру ()

.

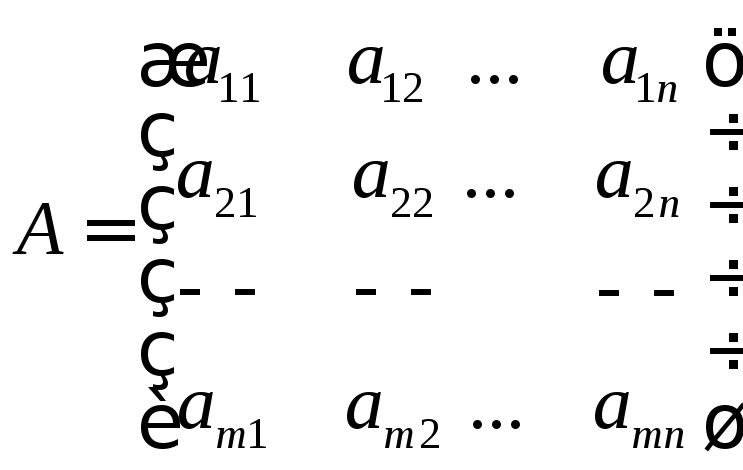З матрицею А пов’язані дві системи векторів: система - вимірних векторів-рядків і система - вимірних ректорів стовпців . Ранг першої системи називають рядковим рангом матриці А, ранг другої системи — стовпцевим рангом. Рядковий ранг матриці А є максимальне число лінійно незалежних рядків, а стовпцевий ранг – максимальне число лінійно незалежних стовпців.

Теорема 3. Рядковий і стовпцевий ранги будь-якої матриці рівні.

Нехай система векторів-рядків матриці А має ранг , а система векторів-стовпців має ранг , причому нехай . Припустимо, що базисом векторів-рядків будуть вектори , а базисом векторів-стовпців – , тобто базисні вектори розміщені у лівому верхньому куту матриці А

. (13)

Якщо матриця А спочатку не має вигляду (13), то переставляючи рядки і стовпці, завжди можна привести її до такого вигляду. Ранг системи векторів-рядків і векторів-стовпців при цьому не змінюється.

Розглянемо систему „вкорочених” векторів :

і утворимо систему однорідних лінійних рівнянь, яку запишемо у векторно-скалярній формі

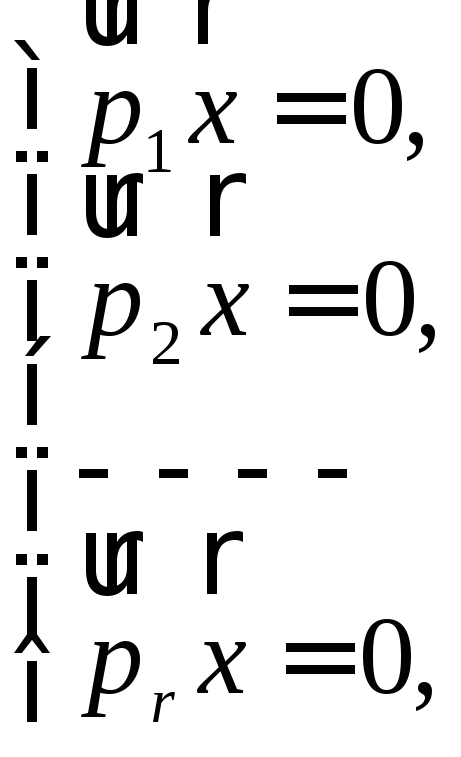
(14)

Оскільки в цій системі невідомих більше, ніж рівнянь – , то система (14) матиме ненульовий розв’язок

.

Вектори збігаються з базисом системи векторів-рядків. Тому “вкорочені” вектори можна лінійно виразити через :

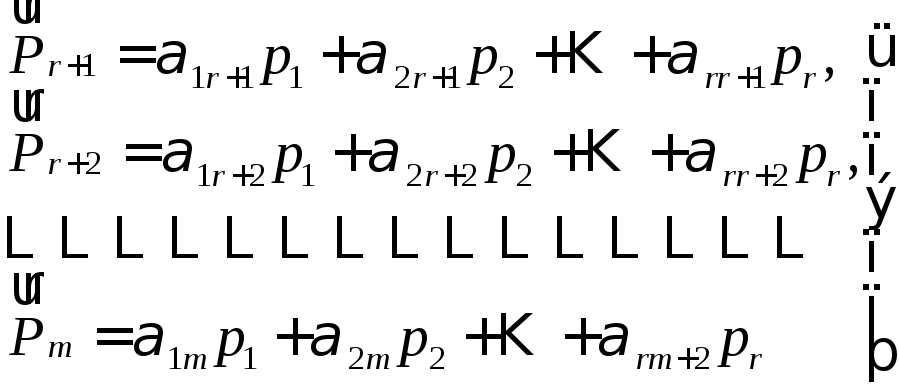(15)

Помножимо вектор скалярно на , отримаємо: . Звідси, враховуючи (14), дістаємо . Аналогічно з рівності (15) знаходимо систему лінійних однорідних рівнянь

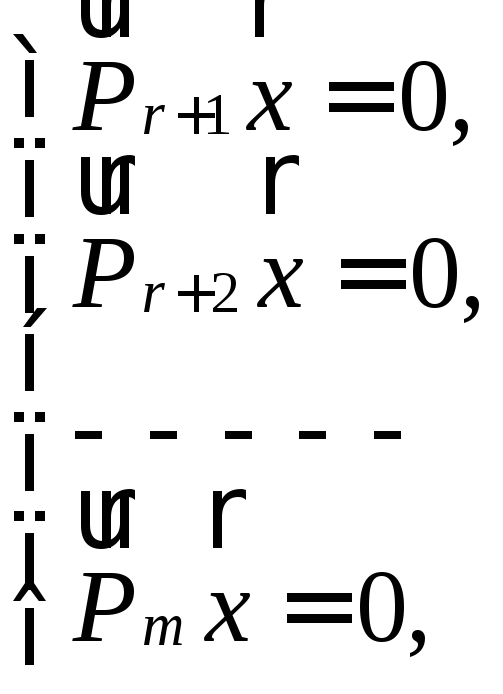(16)

Яка має ненульовий розв’язок . Оскільки розв’язок системи (14) і (16), то він буде розв’язком об’єднаної системи

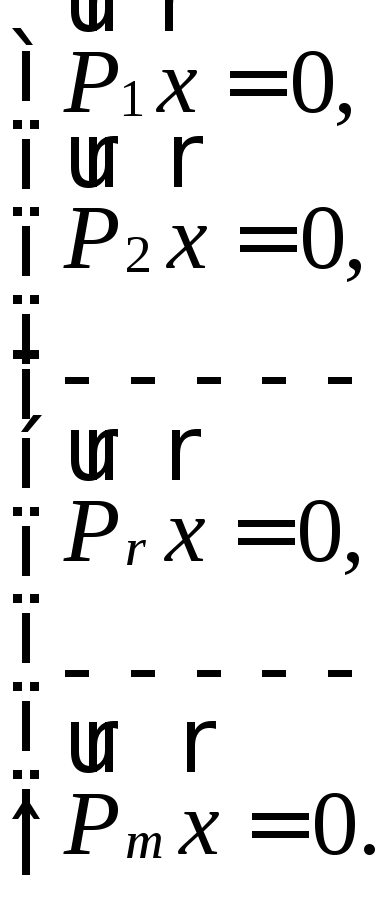(17)

Систему (17)запишемо у вигляді

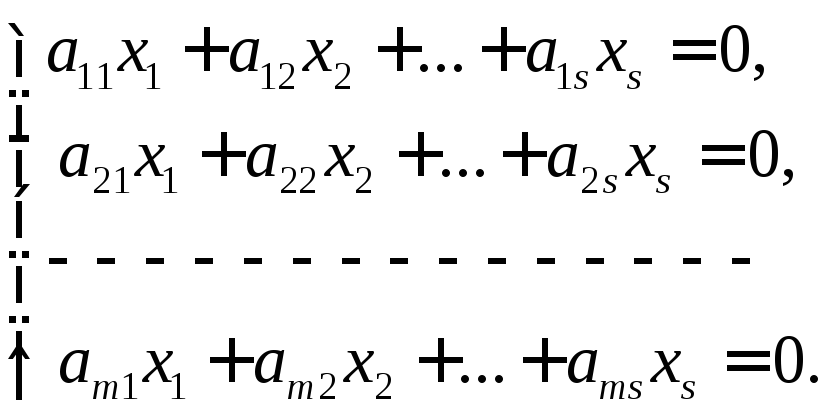
або у векторній формі – Тому маємо рівність , тобто вектори лінійно залежні, всупереч припущенню. Отже, припущення, що неправильне. Аналогічно можна переконатись, що неправильним буде припущення . Тому залишається, правильним, що .

Означення. Рангом матриці називається ранг системи її векторів-рядків, або векторів-стовпців.

Ранг матриці належить до числа її важливих характеристик. Щоб обчислити ранг матриці досить обчислити ранг множини векторів-рядків, або векторів-стовпців.

Будь-яке елементарне перетворення матриці не змінює її рангу. Ранг ступінчастої матриці дорівнює числу її ненульових рядків. Ранг матриці А позначатимемо rank А або r(А).

Приклад. Знайти ранг матриці

За допомогою елементарних перетворень рядків перетворимо матрицю А в ступінчасту.

Ранг ступінчастої матриці дорівнює 3, а отже, і ранг матриці А дорівнює 3. ( r (A)=3).