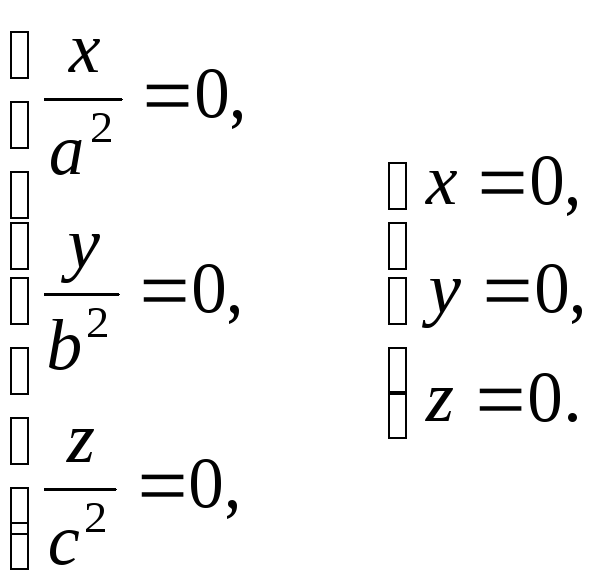
Отже, ми переконалися, що точка є єдиним центром еліпсоїда, заданого канонічним рівнянням.

П р и к л а д  2. Знайти центр гіперболічного циліндра

.

Р о з в ’ я з а н н я.

Для цієї поверхні

.

Із формули (3) маємо:

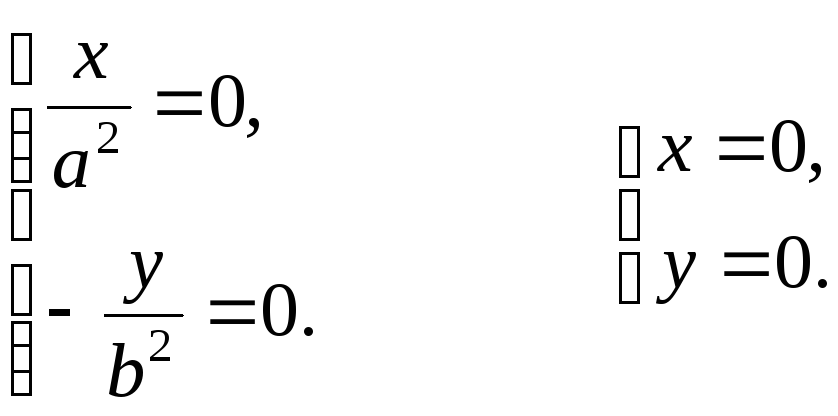
а це є рівняння координатної осі .

Отже, гіперболічний циліндр має пряму центрів.

П р и к л а д 3. Знайти центр поверхні

.

Р о з в ’ я з а н н я.

Зауважимо, що це – вироджена поверхня другого порядку, що розпадається на пару паралельних площин:

Для цієї поверхні

За формулами (3) маємо:

.

Отже, ця поверхня має площину центрів.

П р и к л а д 4. Знайти центр гіперболічного параболоїда .

Р о з в ’ я з а н н я.

Перепишемо рівняння так:

.

Тоді . За формулами (3) маємо:

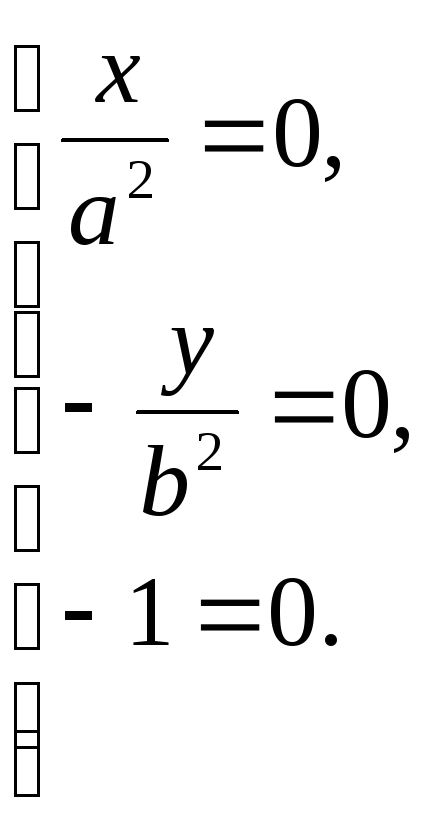
Система розв’язків не має, отже, гіперболічний параболоїд не має центра.

Якщо система (3) має тільки один розв’язок, а відповідно поверхня (1) має тільки один центр, то вона називається центральною. До таких поверхонь належать еліпсоїд, однопорожнинний і двопорожнинний гіперболоїди, конус.

Якщо ж ця система має безліч розв’язків, то можливі два випадки:

1. Ця поверхня має лінію центрів, тобто всі її центри розміщені на прямій. Це буде тоді, коли одне рівняння системи (3) є наслідком двох інших рівнянь. Відповідними поверхнями є еліптичний і гіперболічний циліндри, пара площин, що перетинаються.

2. Якщо два рівняння системи (3) є наслідками третього рівняння, то тоді поверхня має площину центрів. Такою поверхнею є пара паралельних площин.

Якщо поверхня не має центра, то вона називається нецентральною. Такими поверхнями є еліптичний і гіперболічний параболоїди.

§14. Дотична площина до поверхні другого порядку Нехай поверхня другого порядку задана загальним рівнянням

(1)

а точка лежить на цій поверхні.

Т е о р е м а. Геометричне місце прямих, які проходять через точку і дотикаються до поверхні в цій точці, є площина. Ця площина називається дотичною площиною до поверхні в точці.

Д о в е д е н н я.

Запишемо рівняння деякої прямої, що проходить через точку :

(2)

Знайдемо координати точок перетину поверхні (1) і прямої (2). Для цього підставимо (2) в (1) і скористаємося позначеннями, введеними в § 12. Матимемо:

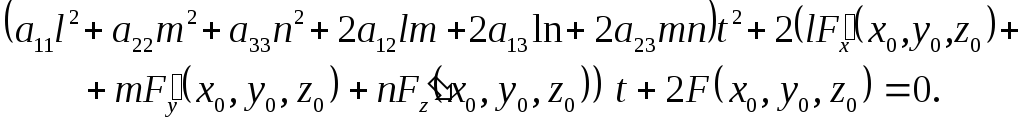(3)

Оскільки точка лежить на поверхні (1), тоі рівняння (3) запишеться у вигляді

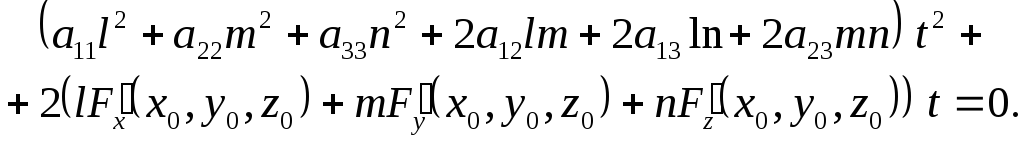(4)

Пряма (2) дотикається до поверхні (1) у точці тоді і тільки тоді, коли це квадратне рівняння має два корені, які збігаються, тобто коли

(5)

Виключаючи з (2) і (5), ми замінюємо координати напрямних векторів дотичних прямих пропорційними їм різницями, які містять змінні координати точок дотичних, тобто знаходимо рівняння геометричного місця дотичних:

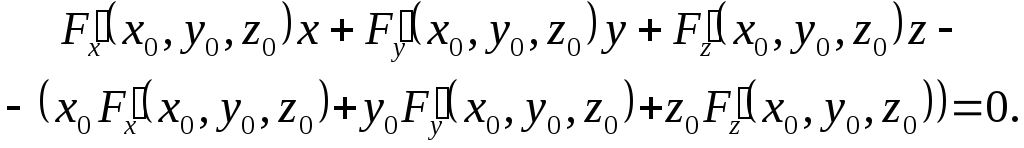(6)

Перетворимо вираз у дужках:

.

Підставивши у (6), матимемо

(7)

або

(8)

Це рівняння лінійне. Отже, геометричне місце дотичних до поверхні другого порядку в точці є площина. Теорему доведено.

Рівняння (7), (8) – рівняння дотичної площини до поверхні (1) у точці .

П р и к л а д 1. Записати рівняння дотичної площини до еліпсоїда у його точці.

Р о з в ’ я з а н н я.

Для еліпсоїда . За формулою (7)

,

або

.

П р и к л а д 2. Записати рівняння дотичної площини до еліптичного параболоїда .

Р о з в ’ я з а н н я.

Для цієї поверхні

.

За формулою (7):

,

або

.

Пропонуємо самостійно переконатися, що дотичною площиною

• до однопорожнинного гіперболоїда 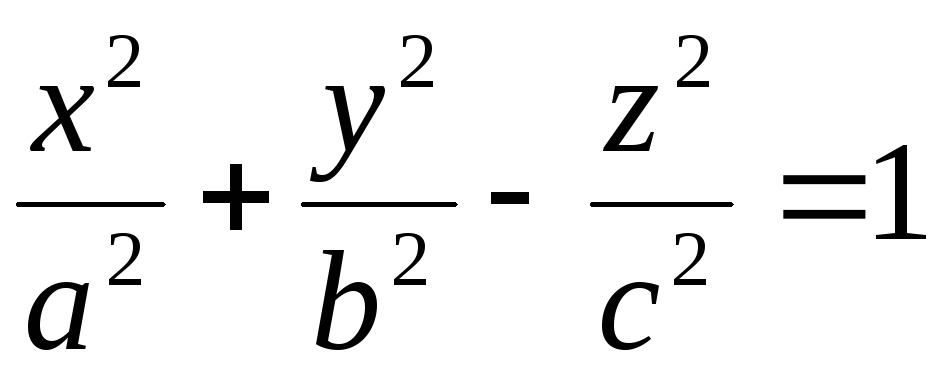є площина;

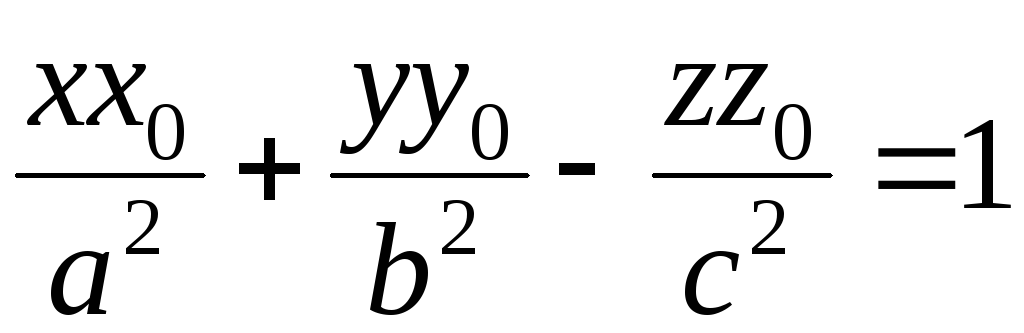• до двопорожнинного гіперболоїда 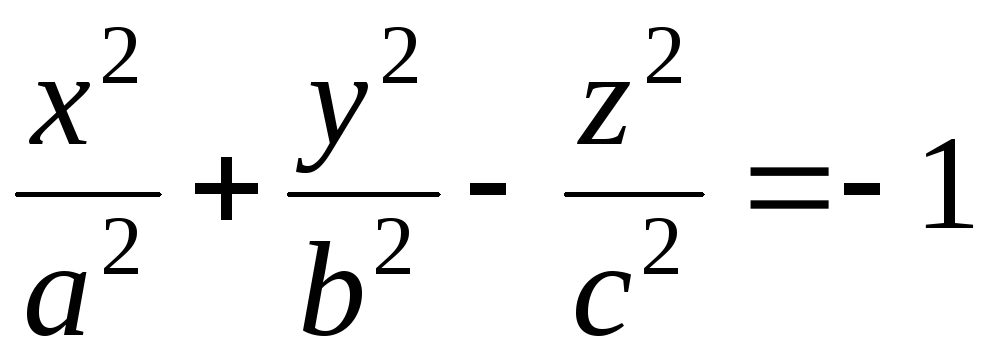–площина;

• до гіперболічного параболоїда – площина;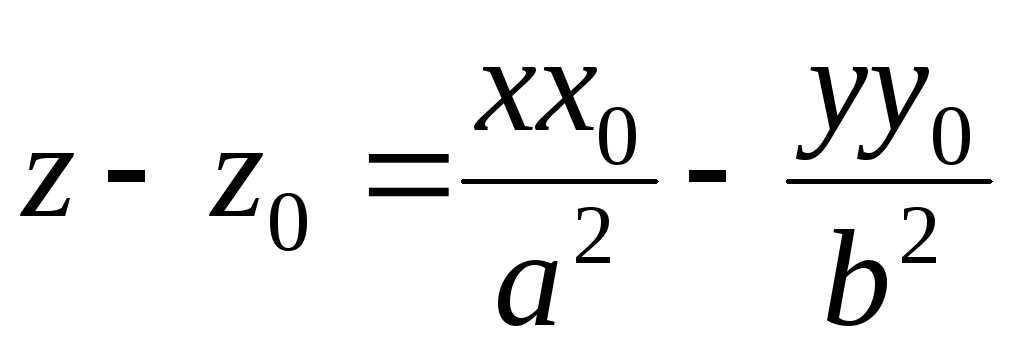

• до конічної поверхні 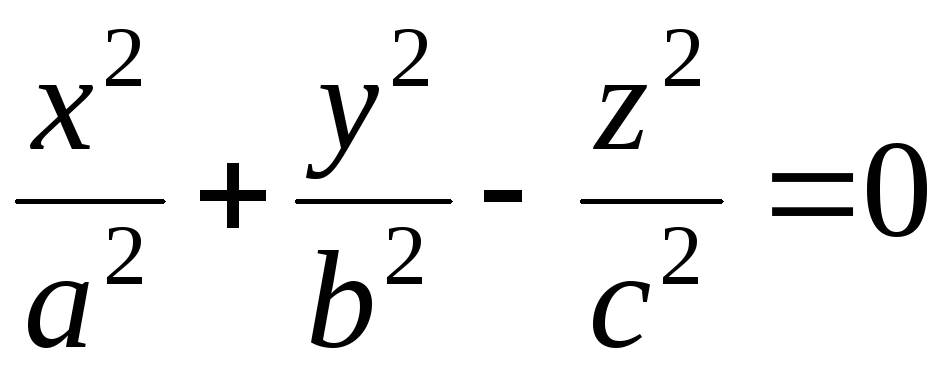– площина.

§ 15. Площини симетрії поверхні другого порядку

Означення. Площина називаєтьсяплощиною симетрії поверхні, якщо разом з довільною точкою М цій поверхні належить і точка , симетрична точціМ відносно площини .

Нехай у деякій прямокутній системі координат поверхня другого порядку задана загальним рівнянням

(1)

Нехай ця поверхня має площину симетрії, нормальний вектор якої (рис. 15.1). Тоді ця площина симетрії буде діаметральною площиною, спряженою з напрямком, який задається вектором. Тому її рівняння запишеться так:

,

або

;

.

Коефіцієнти при змінних у цьому рівнянні є координатами нормального вектора до даної площини, який буде колінеарним до вектора, тому координати цих векторів пропорційні. Отже, справджується така рівність:

.

Звідси, беручи до уваги, що , дістанемо:

(2)

Ця система матиме ненульовий розв’язок відносно (А,В,С) тоді і тільки тоді, коли її визначник дорівнює нулю:

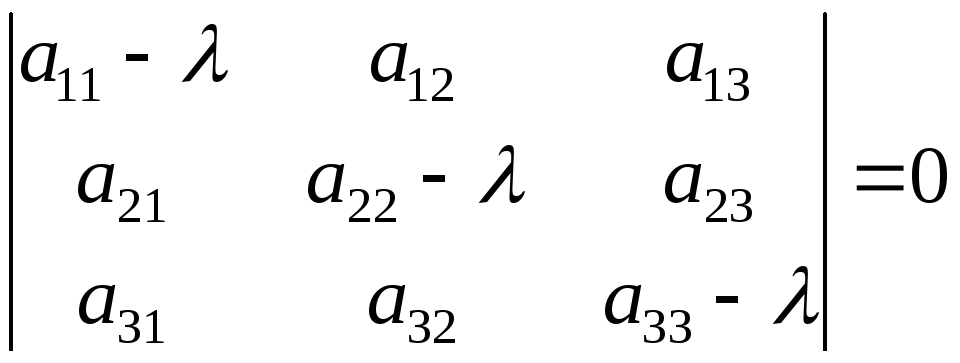(3)

Рівняння (3) називається характеристичним рівнянням даної поверхні.

Оскільки матриця , є симетричною, то, як відомо з алгебри, її власні числа (корені рівняння (3)) будуть дійсними. Розв’язавши рівняння (3) і знайшовши його корені, необхідно підставити їх по черзі в систему (2). Розв’язуючи систему (2) для кожногознайдемо координативідповідних нормальних векторів площин симетрії. Залежно від того, скільки розв’язків має система (2), поверхня може мати різну кількість площин симетрії або не мати жодної.

Знайшовши координати вектора , одразу можна записати рівняння площини симетрії як відповідної діаметральної площини.

П р и к л а д. Знайти площини симетрії поверхні

.

Р о з в ’ я з а н н я.

1. Складемо і розв’яжемо характеристичне рівняння

;

;

;

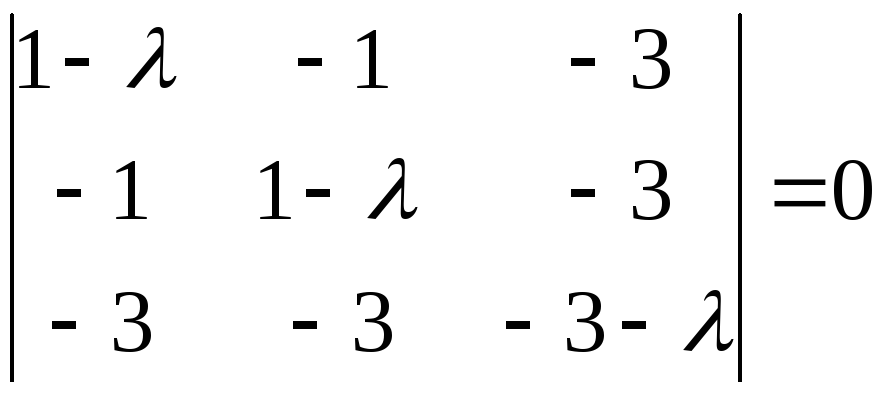Отже, .

2. Для кожного з коренів характеристичного рівняння знаходимо із системи (3) відповідний нормальний вектор шуканої площини симетрії

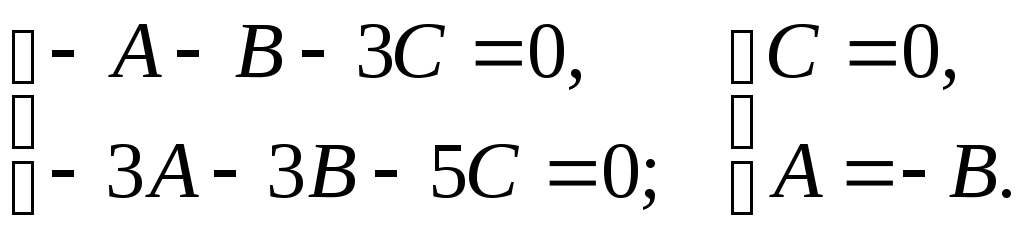
Нехай .

Отже, .

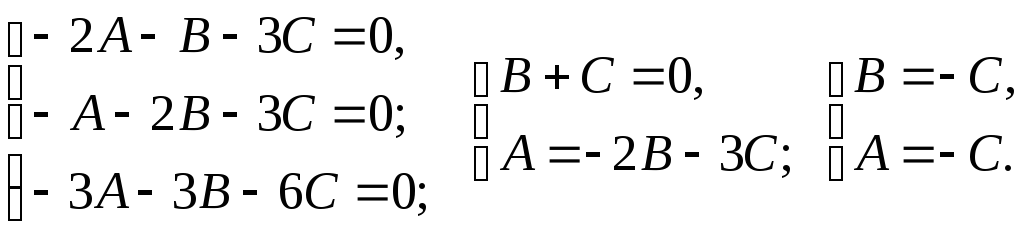
Нехай , тоді,.

Нехай , тоді.

3. Записуємо рівняння площини симетрії як рівняння діаметральних площин, спряжених до знайдених напрямків (формула (8) § 12). Для цієї поверхні

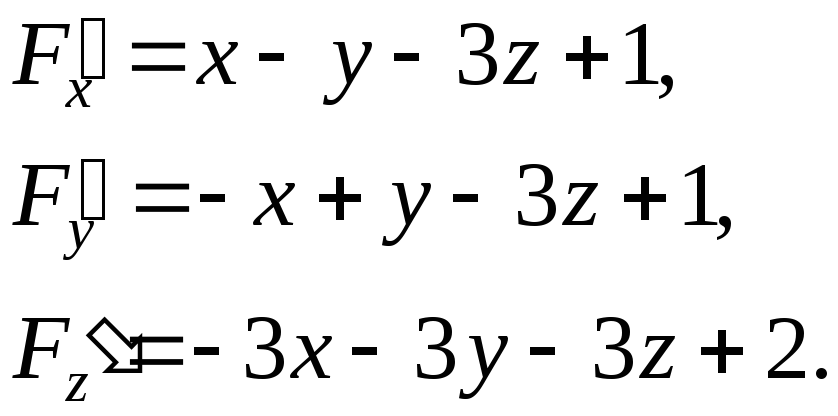
Тому рівняння площини симетрії такі:

1) ;

;

.

2) .

;

.

3) .

;

.

Відповідь: .