§ 16. Зведення загального рівняння поверхні другого порядку до канонічного вигляду

Нехай у деякій прямокутній системі координат поверхня другого порядку задана загальним рівнянням

(1)

Розглянемо вираз

, (2)

який називається квадратичною формою даної поверхні.

Введемо позначення

.

Тоді вираз (2) можна записати у вигляді . Дійсно

.

Таким чином,

. (3)

Поставимо тепер завдання знайти таку нову систему координат , у якій рівняння даної поверхні матиме найпростіший вигляд. Припустимо спочатку, що початки нової і старої систем координат збігаються. Тоді формули перетворення мають вигляд:

(4)

Наша задача полягає в тому, щоб за допомогою перетворення (4) звести квадратичну форму (3) до якомога простішого вигляду. Введемо позначення:

.

Тоді формули (4) запишуться у вигляді

. (5)

Якщо формулу (5) підставити у (3), то квадратична форма зводиться до такого вигляду:

.

Таким чином, в результаті даного перетворення квадратична форма зводиться до іншого квадратичної формиіз зміннимиі новою матрицею.

Тому, щоб звести квадратичну форму (3) до найпростішого вигляду, треба підібрати перетворюючу матрицю С таким чином, щоб матриця мала найпростіший вигляд.

Виявляється, що матриця матиме найпростіший вигляд, якщо її стовпцями будуть власні вектори матриціА, які відповідають власним значенням . При цьому необхідно, щоб ці власні вектори утворювали ортонормований базис.

Дійсно, нехай

є власними векторами матриці А, які відповідають її власним значенням . Це означає, що виконуються рівності. Оскільки матрицясиметрична, то вектори– ортогональні. Будемо вважати, що вони одиничні. Складемо матрицюС з координат цих векторів

.

Тоді

Таким чином, у новій системі координат координатними векторами якої є ортонормовані власні вектори матриціА, квадратична форма набуває вигляду

Тому якщо від системи координат перейти до нової системи координат, координатними векторами якої є ортонормована система власних векторів матриціА, то в цій системі рівняння поверхні зведеться до вигляду

.

За допомогою паралельного перенесення системи координат це рівняння можна спростити ще більше. В результаті цього неважко переконатися, що довільна поверхня другого порядку є або еліпсоїдом, або однопорожнинним чи двопорожнинним гіперболоїдом, або еліптичним чи гіперболічним параболоїдом, або конусом, або циліндром, або ж парою площин, які можуть перетинатися, бути паралельними чи збігатися. Причому поверхня може бути і уявною, наприклад, – уявний еліпс,– уявний конус.

З цих міркувань випливає такий алгоритм зведення загального рівняння поверхні другого порядку до канонічного виду:

1. Складаємо характеристичне рівняння поверхні другого порядку (1)

(6)

і знаходимо його корені .

2. Знаходимо власні вектори матриці А, які відповідають знайденим власним значенням, розв’язуючи рівняння:

Оскільки матриця А симетрична, то при різних значеннях коренів рівняння (6) власні вектори будуть попарно ортогональними. Якщо ж система (6) має кратні корені, то для кратного кореня потрібно підібрати відповідні ортогональні власні вектори. У кожному випадку ці вектори потрібно пронормувати, взявши замість них одиничні вектори

3. Складаємо формули переходу від системи координат до нової системи:

в яких коефіцієнти при змінних є координатами знайдених базисних векторів.

4.Підставляємо ці формули у початкове рівняння (1), в результаті чого воно зведеться до вигляду

.

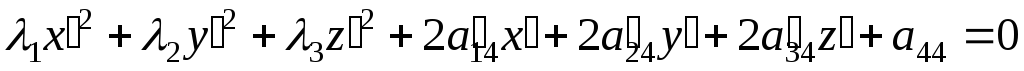5. Виділяючи в одержаному рівнянні повні квадрати і застосовуючи паралельне перенесення системи координат, зводимо рівняння даної поверхні до канонічного вигляду.

П р и к л а д 1. Звести до канонічного вигляду рівняння поверхні

.

Р о з в ’ я з а н н я.

1. Складаємо характеристичне рівняння

;

2. Знаходимо відповідні власні вектори

Якщо , то. Отже,

Якщо В = 1, то .

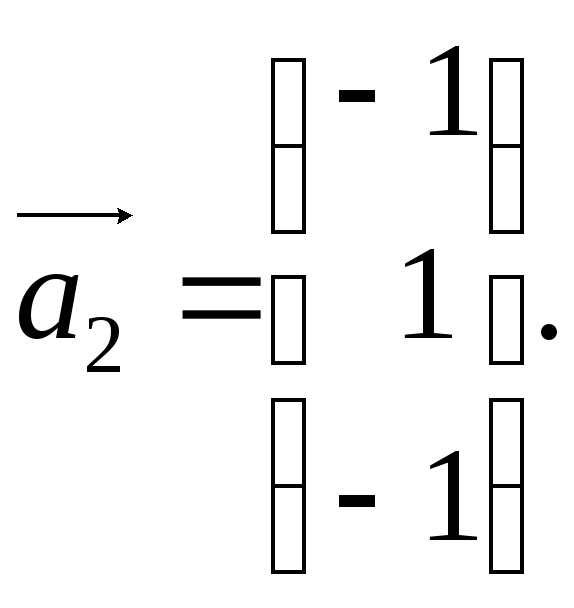
Якщо В = 2, то А = 1, С = 1.

Нормуємо знайдені власні вектори:

Складаємо формули переходу до нової системи координат :

4. Підставивши ці формули в рівняння поверхні, дістанемо

5.Виділимо повні квадрати:

Застосувавши паралельне перенесення

або

отримаємо , або.

Таким чином, дана поверхня – еліптичний параболоїд.

П р и к л а д 2. Звести до канонічного вигляду рівняння поверхні

Р о з в ’ я з а н н я.

1. Складаємо і розв’язуємо характеристичне рівняння

.

2. Знаходимо відповідні власні вектори:

.

Власні вектори мають координати:

.

Нехай тоді

Якщо тоді

Ортогоналізуємо ці вектори.

Нехай 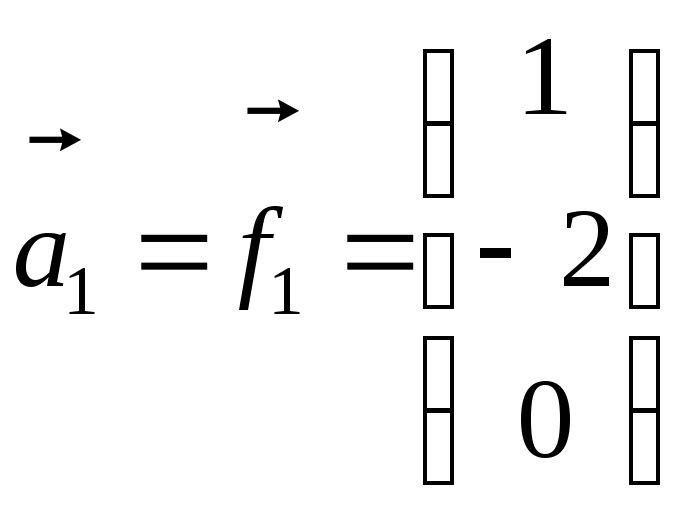., причому, тобто, звідки

;

.

Отже,

Нехай С= –2, тоді .

Нормуємо знайдені власні вектори:

3. Складаємо формули переходу до нової системи координат :

4. Підставимо ці формули у рівняння поверхні:

4. Виділимо повні квадрати

.

Застосувавши паралельне перенесення

або

в новій системі отримаємо рівняння:

або

Отже, дана поверхня – круговий конус.