6. Фундаментальна система розв’язків лінійної однорідної системи рівнянь

Нехай дано довільну систему лінійних однорідних рівнянь

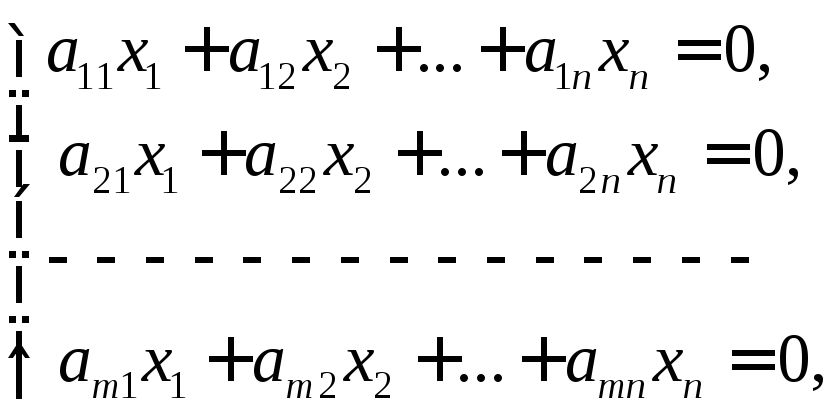(21)

Як уже зазначалося в п.2 §5, ця система сумісна: вона має нульовий розв’язок . Це узгоджується з теоремою Кронекера-Капеллі: ранг матриці і ранг розширеної матриці цієї системи рівні, оскільки приєднання до матриці системи стовпця вільних членів, що складається з нулів, не може збільшити її рангу.

Якщо ранг матриці системи (21) дорівнює , то, за критерієм визначеності, вона має єдиний розв’язок – нульовий.

Якщо ранг матриці системи (21) менший ніж , то система має нескінченну множину рядків і, отже, має розв’язки, відмінні від нульового.

Якщо в системі лінійних однорідних рівнянь (21) число рівнянь менше, ніж число невідомих, то система (21) неодмінно має ненульові розв’язки, оскільки ранг матриці такої системи не може дорівнювати числу невідомих.

Розв’язки системи (21) розглядатимемо як вектори з простору .

Теорема 6. Якщо вектори і є розв’язками системи лінійних однорідних рівнянь (21), то їхня сума також є розв’язком цієї системи.

Запишемо систему (21) у векторній формі

. (22)

Оскільки вектори і є розв’язками системи (21), то і .

Звідси випливає, що

,

і, отже, – розв’язок системи (21).

Теорема 7. Якщо вектор є розв’язком системи лінійних однорідних рівнянь (21), то вектор , де – будь-який елемент з поля , також є розв’язком цієї системи.

Справді, оскільки вектор є розв’язком системи (21), то .

Тоді , і, отже, вектор є розв’язком системи (21).

З теорем 6 і 7 безпосередньо випливає твердження

Наслідок. Якщо – розв’язки системи лінійних однорідних рівнянь (21), то і будь-яка лінійна комбінація

цих розв’язків є розв’язком системи (21).

Справді, в силу теореми 7, кожний з векторів є розв’язком системи (21); в силу теореми 6, сума цих розв’язків знову є розв’язком.

Означення 5. Лінійно залежна система розв’язків однорідної системи (21) називається фундаментальною системою розв’язків цієї системи.

Якщо відома деяка фундаментальна система розв’язків однорідної системи то будь-який її розв’язок можна подати у вигляді лінійної комбінації

(23)

і, навпаки, будь-яка така комбінація є розв’язком однорідної системи. Інакше кажуть, вираз (23) охоплює (при все можливих значеннях параметрів ) всі без виключення розв’язки системи (21). Природно тому назвати його загальним розв’язком системи (21).

Теорема 8. Якщо ранг матриці однорідної системи лінійних рівнянь (21) дорівнює , то фундаментальна система розв’язків системи (21) складається з розв’язків.

Нехай . Розв’язуючи систему (21) методом Гауса, прийдемо до системи ступінчастої форми

(24)

Система (24) має рівнянь. Основних невідомих в системі (24) і вільних невідомих. Припустимо, що вільними є невідомі . Надамо вільним невідомим в системі (24) значень:

Після чого знайдемо із системи значень останніх невідомих . Дістанемо деяких розв’язок вихідної системи (21), позначимо його . Аналогічною, покладаючи і знаходячи відповідні значення його . І так далі. Всього ми дістанемо, таким чином, розв’язків системи (21): .

(25)

Якби вектори були лінійно залежні, то лінійно залежними були б і укорочені вектори

відносно них. Система ж одиничних векторів, як відомо, лінійно залежна. Отже, вектори лінійно не залежні і вони складають фундаментальну систему розв’язків однорідної системи (21). Будь-який розв’язок системи (21) дорівнює лінійній комбінації цієї фундаментальної системи

. (26)

Формула 26 задає множину всіх розв’язків системи (21).

Приклад. Знайти фундаментальну систему розв’язків для системи рівнянь і формулу, що задає множину всіх розв’язків цієї системи

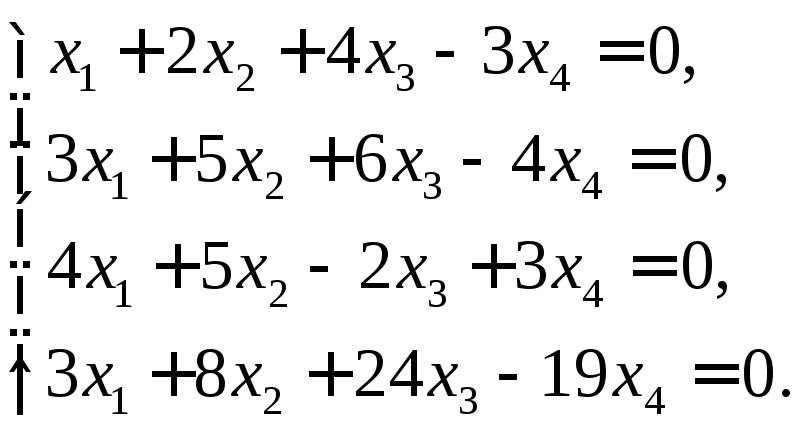(27)

Складемо матрицю з коефіцієнтів при невідомих і зведемо її до ступінчастого вигляду

. Отже, фундаментальна система розв’язків складається з двох розв’язків.

Запишемо ступінчасту систему

Звідси маємо:

Загальних розв’язок подамо у вигляді

.

Надаючи вільним невідомим і значень відповідно та , дістанемо фундаментальну систему розв’язків:

Формула , де – будь-які скаляри задає множину всіх розв’язків системи (27).