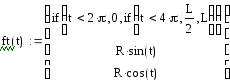Тема 7. Анимация

Mathcad предусматривает возможность анимации графиков и результатов вычислений путем создания AVI-файлов и вставки их в документ Mathcad. Воспроизво­дятся созданные AVI-файлы встроенными в Windows средствами.

Создание анимации

t Mathcad имеет встроенную переменную FRAME, предназначенную только для создания анимационных клипов. FRAME принимает целочисленные значения от 0 до n и должна быть включена в расчетные выражения так, чтобы с изменением FRAME изменялся вид соответствующего графика. Фактически, значением FRAME является номер кадра. Значение переменной FRAME обычно задается не в документе Mathcad,

а в диалоговом окне, открывающемся командой Инструменты ► Анимация► Запись.

0.Перед созданием анимационного клипа убедитесь, что в меню Инструменты (Вычисления) включен режим автоматических вычислений.

Рассмотрим процесс создания анимации.

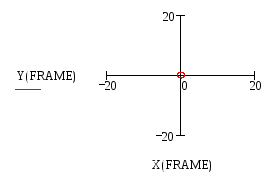
1. Введите переменную Т в математическое выражение, определяющее вид графика-для проверки правильности формулы. Построить график от переменной Frame.

2. Выберите команду Инструменты ► Анимация► Запись.

3. После открытия диалогового окна анимации курсором выделите нужный фраг­мент изображения.

4. В диалоговом окне задайте общее число кадров и частоту их воспроизведения. Установленное по умолчанию число 10 — слишком большая скорость воспро­изведения кадров. Лучше установить 2-3 кадра в секунду, иначе «кино» про­длится всего 1 секунду.

Полученный ролик можно сохранить как AVI-файл и просматривать отдельно от МКАД. При нажатии кнопки Параметры раскрывается список выбора программы сжатия файл.

5. Щелкните на кнопке Анимация и наблюдайте за созданием кадров. Пос­ле завершения этого процесса появится окно проигрывателя видеофайлов.

!При создании клипов рекомендуется отключить автомасштабирование графика. Числовые значения пределов изменения осей следует ввести вручную.

Тема 8. Преобразования матриц. Построение трехмерных графиков

1.Построить пересекающиеся фигуры F1(x,y):=sin(x2+y2) M1=CreateMesh(f,-1.5,1.5,-1.5,1.5,20,40) F2(x,y):=x2+y2-5 M2=CreateMesh(f,-1.5,1.5,-1.5,1.5,20,40)
2. Создать поверхность из функции двух переменных	3. Построить трехмерную кривую
4. Построение цилиндра fi:=0+i2/n	или график FT – тот же вид

1. Построить все трехмерные графики по лекции.

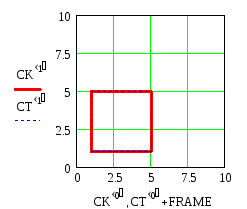
2. Записать в массив координаты окружности, построить график. Используя матрицу поворота, превратить окружность в эллипс. Добавить график эллипса к графику окружности. Параллельно перенести обе фигуры.

3. Построить график квадрата, предварительно сохранив его координаты в массиве.

Используя матрицу поворота, превратить квадрат в ромб. Добавить график ромба к графику квадрата. Параллельно перенести обе фигуры.

Алгоритм выполнения задания 2

Задать n– количество точек рассчитываемых узлов фигуры.

Ввести дискретную переменную .

Задать вектор изменения угла - изменяется в пределах от -до +, т.е. 2.

Задать векторы изменения координат

Задать промежуточные векторы, из которых составить матрицу С.

Задать матрицу поворота и искажения , причем численные значения можно варьировать для получения разных форм эллипса.

Умножить матрицы и построить в одной координатной системе окружность и эллипс.

Алгоритм выполнения задания 3

Задать n– количество точек рассчитываемых узлов фигуры,a- длина ребра,xn,yn– координаты левой нижней вершины .

Ввести дискретную переменную .

Задать векторы изменения координат xиyдля левого вертикального ребра, из которых составить матрицу С1. Матрицу С3 (правая вертикаль) получить из С1 – параллельным переносом. Задать векторы изменения координатxиyдля горизонтального нижнего ребра, из которых составить матрицу С4. Матрицу С2 (верхняя горизонталь) получить из С4.

Объединить все матрицы С в одну К – квадрат, построить график. Задать матрицу поворота и искажения. Повернуть на 45 градусов и сохранить в матрицу R, построить график.

Преобразования матриц

Матрица параллельного переноса теперь определяется как [ 1 0 0 dx ] [ 0 1 0 dy ] [ 0 0 1 dz ] [ 0 0 0 1 ] Матрицу масштабирования можно определить и для матриц 3x3, и для матриц 4x4: [ kx 0 0 ] [ kx 0 0 0 ] [ 0 ky 0 ] или [ 0 ky 0 0 ] [ 0 0 kz ] [ 0 0 kz 0 ] [ 0 0 0 1 ] где kx, ky, kz - коэффициенты масштабирования по соответствующим осям.

Вспомним о матрицах и векторахУдобство матриц для нас заключается как раз в свойстве A*(B*C) = (A*B)*C.Пусть мы делаем несколько поворотов подряд, например, пять (как раз столько, сколько надо для поворота относительно произвольной оси), и пусть они задаюся матрицами A, B, C, D, E (A - матрица самого первого поворота, E - последнего). Тогда для вектора p мы получаем p' = E*(D*(C*(B*(A*p)))) = E*D*C*B*A*p = (E*D*C*B*A)*p = = (E*(D*(C*(B*A))))*p = T*p, где T = (E*(D*(C*(B*A)))) матрица преобразования,являющегося комбинацией пяти поворотов.

Посчитав один раз эту матрицу, можно в дальнейшем без проблем применить довольно сложное преобразование из пяти поворотов к любому вектору с помощью всего одного умножения матрицы на вектор.

Таким образом, можно задать любой поворот матрицей, и любая комбинация поворотов также будет задаваться матрицей, которую можно довольно легко посчитать. Но есть еще параллельный перенос, есть еще масштабирование. Что делать с ними?

На самом деле, эти преобразования тожелегкозаписываются в виде матриц. Только вместо матриц 3x3 и 3-мерных векторовиспользуютсятак называемыеоднородные 4-мерные координаты и матрицы 4x4. При этом вместо векторов вида [ x ] [ y ] [ z ] используются вектора вида [ x ] [ y ] [ z ] [ 1 ] а вместо произвольных матриц 3x3 используются матрицы 4x4 такого вида: [ a b c d ] [ e f g h ] [ i j k l ] [ 0 0 0 1 ] Видно, что если d = h = l = 0, то в результате применения всех операций получается то же самое, что и для матриц 3x3.

и внимательно посмотрим на выведенные формулы для поворота. Можно заметить, что

[ x' ] = [ cos(alpha) -sin(alpha) 0 0] [ x ] [ y' ] = [ sin(alpha) cos(alpha) 0 0] [ y ]

[ z' ] = [ 0 0 1 0] [ z ]

[ 1 ] = [ 0 0 0 1] [ 1 ]

То есть поворот на угол alpha задается одной и той же матрицей, и с помощью этой матрицы (умножая ее на вектор-точку) можно получить координаты повернутой точки.

Матрица параллельного переноса теперь определяется как [ 1 0 0 dx ] [ 0 1 0 dy ] [ 0 0 1 dz ] [ 0 0 0 1 ] Матрицу масштабирования можно определить и для матриц 3x3, и для матриц 4x4: [ kx 0 0 ] [ kx 0 0 0 ] [ 0 ky 0 ] или [ 0 ky 0 0 ] [ 0 0 kz ] [ 0 0 kz 0 ] где kx, ky, kz - коэффициенты масштабирования по [ 0 0 0 1 ] соответствующим осям. Таким образом, получаем следующее.Любое нужное нам преобразование пространства можно задать матрицей 4x4 определенной структуры, разной для разных преобразований.Результатпоследовательного выполнений нескольких преобразований совпадает с результатом одного преобразования T, которое также задается матрицей 4x4, вычисляемой как произведение матриц всех этих преобразований.Важен порядок умножения, так как A*B != B*A. Результат применения преобразования T к вектору [x y z] считается как результат умножения матрицы T на вектор [x y z 1]. Вот и все.

Инженерная задача

Станок в процессе работы испытывает деформации. Станок можно разбить на взаимосвязанные подсистемы. Деформации передаются от одной к другой подсистеме, от резца к заготовке. Поэтому вместо идеального цилиндра после обработки получают сложную искривленную в пространстве фигуру. Деформации каждой подсистемы можно описать. Поэтому можно рассчитать отклонение получаемой после обработки детали от идеальной фигуры. Кроме того, в МКАД можно и наглядно показать получаемую фигуру.

Представим станок в виде основных подсистем

Подсистема	Деформации
резец	поворот вокруг Z
державка резца	перемещение по X, поY, поворот вокругZ, поворот вокругX
суппорт	перемещение по X, перемещение поX, поY
винт суппорта	перемещение по X
передняя бабка	поворот вокруг Z
шпиндель	поворот вокруг Z, поворот вокругY, перемещение поX
патрон	перемещение по X, поворот вокругZ, поворот вокругY
заготовка	поворот вокруг Z

Каждую деформацию задают в виде матрицы.

Зададим матрицу смещения

- матрица со смещением

Зададим матрицы поворота
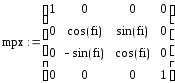