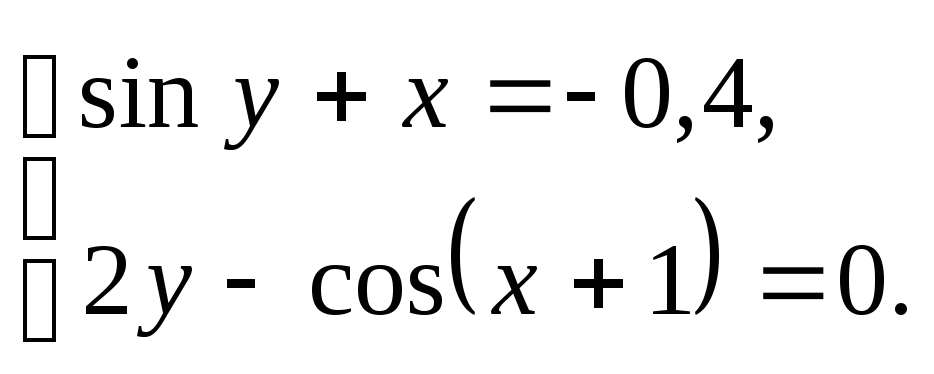Самостоятельно: Построить графики. Найти координаты пересечения двух фигур, если дано:

№ варианта	a	b	R	r	c	d		dx	dy
1	20	40		10				20	30
2				15		40	60	30	5
3			75	25				60	20
4	25	38				38	45	30	20
5	25	50		15				33	-17
6	15	25				40	60	23	-17
7	15	25				40	60	10	39
8						40;20	60	5	35
9	25;10	38;20						20	40
10	25;10	38;20						10	32
11			40		55			45	40
12			40		60			20	10
13	25	38			40			30	-10
14			30			40	45	32	32
15	25	38		18				27	15

Обозначения:

а – малая полуось эллипса;

b – большая полуось эллипса;

R – радиус большой окружности;

r – радиус малой окружности;

c –сторона квадрата;

d –сторона ромба;

 - угол при острой вершине ромба.

1

2

3

4

5

6

7

8

9

10

11

12

13

13

14

15

Тема 6. Задания на решение систем уравнений

1. Решить систему линейных уравнений (Таблица1):

1. используя функцию Find;

2. используя функцию lsolve.

Функция lsolve(M, v) : Возвращается вектор решенияzтакой, чтоM  z = v.

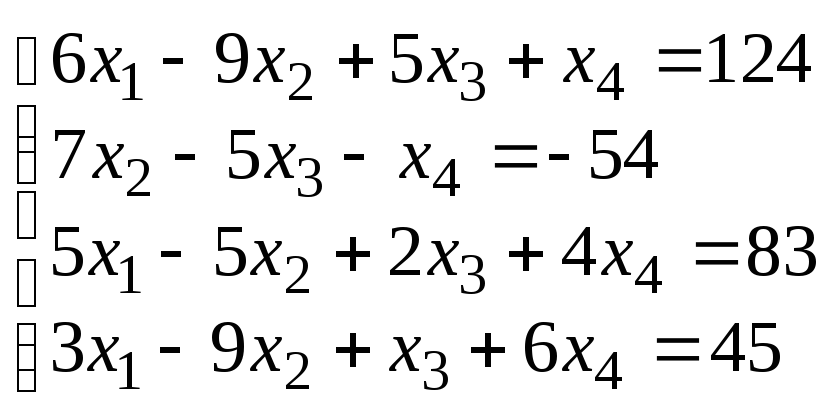
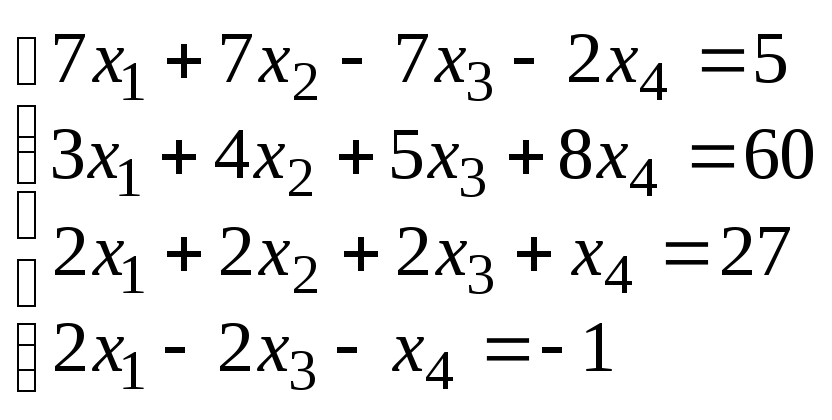
2. Преобразовать нелинейные уравнения системы из Таблицы 2 к видуf ₁(x) = yиf ₂ (y)= x. Построить их графики и определить начальное приближение решения. Решить систему нелинейных уравнений с помощью функцииMinerr.

Таблица 2

№ вари-анта	Система нелинейных уравнений	№ вари-анта	Система нелинейных уравнений

3.Найти корни полинома

Любое уравнение Р(х)=0, где Р(х) – многочлен, отличный от нулевого, называется полиномомотносительно переменной х.

Для нахождения корней выражения, имеющего вид

,

лучше использовать функцию polyroots, нежелиroot. В отличие от функцииroot, функцияpolyroots не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные.

polyroots(v) - Возвращает корни полинома степениn. Коэффициенты полинома находятся в вектореvдлиныn + 1. Возвращает вектор длины n, состоящий из корней полинома.