Тема 4. Векторы

В MathCAD принято считать, что вектор – столбец данных, имеющих индекс – номер элемента по порядку, начиная с нулевого элемента.

Для доступа к данным, находящимся в определенном элементе массива, указывается имя массива и порядковый номер этого элемента, называемый индексом.

Создание матрицы - 3 способа

1. Заполнением шаблона, вызванного из панели Векторы и матрицы с указанием числа строк и столбцов, содержащего пустые места ввода чисел – для небольших массивов.

2. Считыванием данных из файла функцией F:=READPRN(“MIU”)

3. Использованием дискретной переменной – в случае, когда есть формула для вычисления элементов массива.

Один элемент вектора, матрицы можно ввести вручную, задав имя, символ [ или указав индекс. Индексы в матрицах разделяются запятой.

Нижняя граница индексации массива определена системной переменной ORIGIN.По умолчанию ORIGIN =0. Индексы могут быть только целыми, положительными, включая 0.

Следует учесть, что в алгоритмы некоторых встроенных функций обработки массивов заложен ORIGIN =0, а иначе – выдается сообщение об ошибке.

Создание вектора - 3 способа

1. Использованием дискретной переменной – в случае, когда есть формула для вычисления элементов массива – способ используется для построения графиков.

n:=100 i:=0..n-1 x_i :=10+3*i - в вектор x занесены координаты по оси абсцисс.

2. Заполнением поэлементно, вызвав кнопкой панели Матрица форму для заполнения, указав количество строк = 1 и требуемое количество столбцов. Затем следует заполнить строку и ее транспортировать.

3. Заполнением вручную, поэлементно, через символ запятая.

y_i:=5,6,90 – в вектор у занесены координаты по оси ординат.

4. Присвоением значений функции f(t):=5t²+3 y_i:=f(x_i)

Встроенные функции для определения параметров матриц

Rows(M) - строк

Cols(M)- столбцов

Last(M) индекс последнего элемента

Max(M) min(M) макс-мин значения массива

Образование новых матриц из существующих

Augment(A,B) – объединяет матрицы А, В с одинаковым числом строк «бок о бок».

Stack(A,B) – объединяет матрицы А,В с одинаковым числом столбцов друг над другом.

Submatrix(A,irows,jrows,icols,jcols) – создает матрицу, вырезанную из матрицы А от ряда irows до ряда jrows и от столбца icols до столбца jcols.

Сортировка векторов и матриц

Sort(v) – сортировка элементов вектора в порядке возрастания

Reverse(v) – перестановка элементов вектора в обратном порядке

Csort(v) – перестановка строк матрицы М в порядке возрастания элементов i-го столбца

Rsort(M,i) - перестановка столбцов матрицы М в порядке возрастания элементов i-й строки

1.Построить график прямоугольника со сторонами a,b, предварительно сохранив его координаты в массиве.

Задать n – количество точек рассчитываемых узлов фигуры, a, b - длины ребер, xn, yn – координаты левой нижней вершины . Ввести дискретную переменную . Задать векторы изменения координатx и y для каждой вершины. x₀:=10 y₀:=20 x₁:=60 y₁:=100 x₂:=160 y₂:=10

2. Записать в массив координаты окружности, построить график.

Алгоритм выполнения задания 2

Задать n – количество точек рассчитываемых узлов фигуры. Ввести дискретную переменную .

Задать вектор изменения угла - изменяется в пределах от - до +, т.е. 2.

Задать векторы изменения координат

Построить график у от х

Тема 5. Решение уравнений средствами Mathcad

Задача нахождения корня уравнения f(x) = 0 итерационными методами состоит из 2-х этапов:

• отделение корней - отыскание приближенного значения корня (например, графическим методом)

(найти достаточно тесные промежутки, в которых находится корень, иначе говоря, определить интервалы изоляции корня);

Для простейших уравнений вида f(x) = 0 решение находится с помощью функции root.

root(f(z), z) Возвращает значение z, при котором выражение или функция f(z) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр.

Первый аргумент - или функция, определенная где-либо в рабочем документе, или выражение. Второй аргумент - имя переменной, которая используется в выражении. Этой переменной перед использованием функции root необходимо присвоить числовое значение.

Пример 1.x³-5x-1=0

Начальное приближение x1:=0

Решение f(x)= x³-5x-1 x:=-3,-2.9..3

r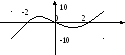oot(f(x1),x1)=-0.202

Другие корни

X:=5 x0:= root(f(x),x) x0=2.33

X:=-10 x0:= root(f(x),x) x0=-2.128

2 способ. Заданием интервала поиска корней

root(f(x),x,-5,-1)=-2.128

root(f(x),x,-1,1)=-0.202

root (f(x),x,1,5)=2.33 Нельзя root (f(x),x,-3,1)

Важно! Если функция имеет малый наклон вблизи корня, то функция root(f(x),x) может сходиться далеко от значения корня. В таком случае следует уменьшить значение погрешности вычислений, задаваемое встроенной переменной TOL.

Пример. Найти решение уравнения

Выражение, стоящее в левой части уравнения, можно представить в виде разности двух функций f(x)-g(x)=0, Тогда f(x)=g(x), а точка, в которой графики этих функций пересекаются, и является графическим решением уравнения. Итак, для решения заданного уравнения проделаем следующее:

1. введем f(x) и g(x)

2. определим интервал изоляции корня

3. зададим начальное значение x

4. найдем решение при помощи функции root(f(x)-g(x),x)

f(x):=

root(f(x),x,0,1)=0.578

root(f(x),x,1,2)=1.764

root (f(x),x,5,6)=5.148 Нельзя root (f(x),x,0,2)