Раздел 3. Нормальные формы для формул алгебры высказываний

3.1 Нормальные формы

Нормальная форма – это синтаксически однозначный способ записи формулы, реализующей данную функцию.

Пользуясь известными законами логики, всякую формулу можно преобразовать в равносильную ей формулу вида , гдеи каждое– либо переменная, либо отрицание переменной, либо конъюнкция переменных или их отрицаний. Другими словами, любую формулу можно привести к равносильной ей формуле простого стандартного вида, которой будет являться дизъюнкция элементов, каждый из которых представляет собой конъюнкцию отдельных различных логических переменных либо со знаком отрицания, либо без него.

Пример 3.1: В больших формулах или при многократных преобразованиях принято знак конъюнкции опускать (по аналогии со знаком умножения): _{. Мы видим, что после проведенных преобразований формула представляет собой дизъюнкцию трех конъюнкций.}

Такая форма называется дизъюнктивной нормальной формой (ДНФ). Отдельный элемент ДНФ называется элементарной конъюнкцией или конституентой единицы.

Аналогично любую формулу можно привести к равносильной ей формуле, которая будет являться конъюнкцией элементов, каждый из которых будет представлять собой дизъюнкцию логических переменных со знаком отрицания или без него. То есть, каждую формулу можно привести к равносильной ей формуле вида , гдеи каждое– либо переменная, либо отрицание переменной, либо дизъюнкция переменных или их отрицаний. Такая форма называетсяконъюнктивной нормальной формой (КНФ).

Пример 3.2:

Отдельный элемент КНФ называется элементарной дизъюнкцией или конституентой нуля.

Очевидно, что каждая формула имеет бесконечно много ДНФ и КНФ.

Пример 3.3: Найдем несколько ДНФ для формулы .

1)

2)

3)

4)

5)

3.2 Совершенные нормальные формы

СДНФ (совершенная ДНФ) – это такая ДНФ, в которой каждая элементарная конъюнкция содержит все элементарные высказывания, либо их отрицания по одному разу, элементарные конъюнкции не повторяются.

СКНФ (совершенная КНФ) – это такая КНФ, в которой каждая элементарная дизъюнкция содержит все элементарные высказывания, либо их отрицания по одному разу, элементарные дизъюнкции не повторяются.

Пример 3.3:

_{– СДНФ}

_{– СКНФ}

Сформулируем характерные признаки СДНФ (СКНФ).

1. Различны все члены дизъюнкции (конъюнкции);

2. Различны все члены каждой конъюнкции (дизъюнкции);

3. Ни одна конъюнкция (дизъюнкция) не содержит одновременно переменную и ее отрицание;

4. Каждая конъюнкция (дизъюнкция) содержит все переменные из числа входящих в исходную формулу.

Как мы видим, характерные признаки (но не формы!) удовлетворяют определению двойственности, поэтому достаточно разобраться с одной формой, чтобы научиться получать обе.

Из ДНФ (КНФ) с помощью равносильных преобразований легко можно получить СДНФ (СКНФ). Так как правила получения совершенных нормальных форм также являются двойственными, то подробно разберем правило получения СДНФ, а правило получения СКНФ сформулируйте самостоятельно, используя определение двойственности.

Общее правило приведения формулы к СДНФ с помощью равносильных преобразований:

Для того чтобы привести формулу F, не являющуюся тождественно ложной к СДНФ, достаточно:

1. привести ее к какой-нибудь ДНФ;

2. удалить члены дизъюнкции, содержащие переменную вместе с ее отрицанием (если таковые имеются);

3. из одинаковых членов дизъюнкции (если таковые имеются) удалить все, кроме одного;

4. из одинаковых членов каждой конъюнкции (если такие имеются) удалить все, кроме одного;

5. если в какой-нибудь конъюнкции не содержится переменной 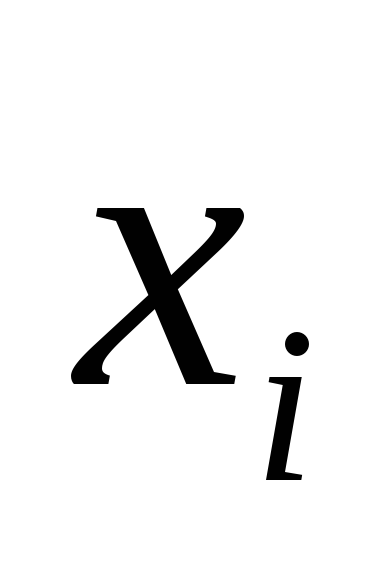из числа переменных, входящих в исходную формулу, добавить к этой конъюнкции член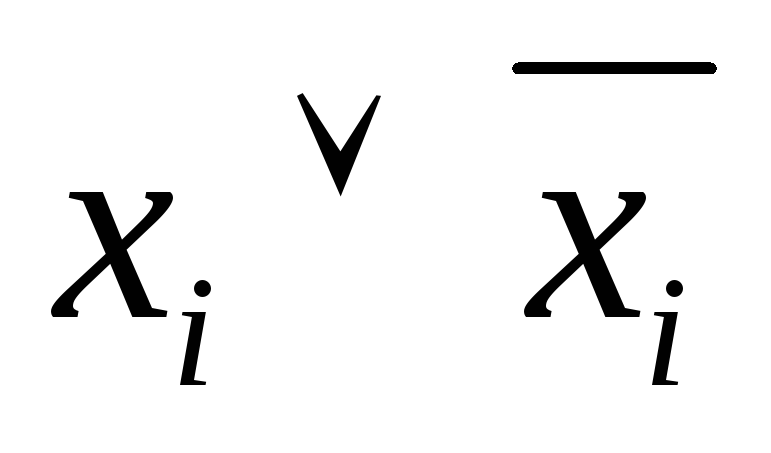и применить соответствующий дистрибутивный закон;

6. если в полученной дизъюнкции окажутся одинаковые члены, воспользоваться предписанием 3.

Полученная формула и является СДНФ данной формулы.

Пример 3.4: Найдем СДНФ и СКНФ для формулы .

Так как ДНФ для данной формулы уже найдена, то начнем с получения СДНФ:

1) ;

2) в полученной дизъюнкции нет переменных вместе с их отрицаниями;

3) в дизъюнкции нет одинаковых членов;

4) ни в одной конъюнкции нет одинаковых переменных;

5) первая элементарная конъюнкция содержит все переменные из числа входящих в исходную формулу, а во второй элементарной конъюнкции не хватает переменной z, поэтому добавим в нее член и применим дистрибутивный закон:;

6) легко заметить, что в дизъюнкции появились одинаковые члены, поэтому убираем один (предписание 3);

Таким образом, получаем СДНФ формулы F: .

Для получения СКНФ воспользуемся 4 вариантом ДНФ (пример 3.3), которую можно также рассматривать как КНФ формулы: .

1) ;

2) полученная конъюнкция не содержит переменных вместе с их отрицаниями;

3) в конъюнкции нет одинаковых членов;

4) так как пока нет дизъюнкций, то в них нет и одинаковых членов;

5) получим первые элементарные дизъюнкции, добавив к переменной х конъюнкцию , а к переменной– конъюнкцию:;

6) в полученной конъюнкции имеются одинаковые члены, поэтому перейдем к предписанию 3;

3) уберем одну из одинаковых дизъюнкций: ;

4) в оставшихся дизъюнкциях нет одинаковых членов;

5) ни в одной из элементарных дизъюнкций нет всех переменных из числа входящих в исходную формулу, поэтому дополним каждую из них конъюнкцией :;

6) в полученной конъюнкции нет одинаковых дизъюнкций, поэтому найденная конъюнктивная форма является совершенной.

Так как в совокупности СКНФ и СДНФ формулы F 8 членов, то скорее всего они найдены верно.

Каждая выполнимая (опровержимая) формула имеет одну единственную СДНФ и одну единственную СКНФ. Тавтология не имеет СКНФ, а противоречие – СДНФ.