5.4.Методы решение логических задач

При решении любой задачи могут быть выделены следующие этапы:

1. Анализ условия задачи ( выделение исходных данных ).

2. Поиск метода решения.

3. Символическая запись задачи.

4. Рассуждения и пояснения к решению.

5. Анализ полученных результатов и запись ответа.

Существует следующая последовательность решения задач с помощью схем:

1. Кратко записать условие, вопрос задачи. Элементы условия задачи отобразить при помощи символьных переменных.

2. Приступить к её решению.

- Если по условию между двумя элементами есть соответствие, то они соединяются сплошной линией.

- Если же между элементами соответствия нет, то они соединяются пунктирной линией.

Чтобы наглядно было видно, какие элементы рассуждений даны, а какие получены по доказательству, можно применять разные цветовые решения ( проводить линии, например, красным (дано) и зелёным (доказательство) карандашами ).

С помощью таблиц решаются задачи с четырьмя, пятью и более парами элементов, когда использование схем неудобно и не наглядно из-за чрезмерной громоздкости.

Задача № 1. Подруги

Света и Наташа имеют фамилии Иванова и Петрова. Какую фамилию имеет каждая девочка, если Света и Иванова живут в соседних домах?

1. Так как Света не Иванова ( по условию ), значит,

Надо: Света - Петрова.

Кто какую фамилию имеет?

2. Так как Света - Петрова ( по доказательству ), значит, Наташа не Петрова.

3. Так как Наташа не Петрова ( по доказательству ), значит Наташа Иванова.

Ответ: Света имеет фамилию Петрова, а Наташа - Иванова.

Задача 2. Виктор, Роман, Юрий и Сергей заняли на математической олимпиаде первые четыре места. Когда их спросили о распределении мест, они дали три таких ответа:

• 1) Сергей - первый, Роман - второй;

• 2) Сергей - второй, Виктор - третий;

• 3) Юрий - второй, Виктор - четвертый.

Как распределились места, если в каждом ответе только одно утверждение истинно?

	1	2	3	4
Виктор			1	0
Роман	-	0		1
Юрий		1
Сергей	1	0	-

Вопросы для контроля:

1. Правило получения следствий из посылок и посылок для данных следствий.

2. Виды текстовых логических задач.

3. Методы решения логических задач.

Раздел 6. Исчисление высказываний.

6.1. Понятие переключательной схемы.

Переключательная схема – это устройство из переключателей (контактов) и проводов, связывающих два полюса – вход и выход. (Полюсов может быть и больше, но мы ограничимся рассмотрением двухполюсных схем.) Для конкретности будем говорить о переключательных схемах, представляющих собой участок электрической цепи, по которому проходит ток от источника А к потребителю В (например, к лампочке). Между источником и потребителем может быть замыкающий и размыкающий цепь контакт либо несколько контактов, соединенных последовательно или параллельно.

Рассмотрим схему с одним контактом (рис.). Цепь замкнута (лампочка горит) в том и только в том случае, если контакт замкнут.

Сопоставим контакту р переменную X, а двум состояниям контакта "замкнут", разомкнут" – соответственно значения 1 и 0 переменной X. Условимся также обозначать утверждение "цепь замкнута" через 1, а утверждение "цепь разомкнута" – через 0; тогда формула X опишет работу данной цепи:

р	X	Цепь
Замкнут	1	Замкнута
Разомкнут	0	Разомкнута

Если между источником и потребителем тока поместить два контакта р₁ и р₂ (рис.), соединенные последовательно, то цепь замкнута, когда оба контакта замкнуты, и разомкнута, когда хотя бы один из них разомкнут. Конъюнкция переменных Х и Y, поставленных в соответствие контактам р₁ и р₂, истинyа, когда обе переменные принимают значение 1, и ложна, когда хотя бы одна из них принимает значение 0. Таким образом, формула соответствует схеме на втором рисунке.

Очевидно, что формула описывает схему с п последовательно соединенными контактами.

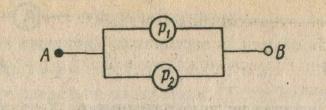
Если контакты р₁ и р₂ соединены параллельно (рис.), то цепь замкнута, когда хотя бы один из контактов замкнут, и разомкнута когда оба они разомкнуты. Такой схеме соответствует формула , являющаяся истинной, когда хотя бы одна из переменных принимает значение 1, и ложной, когда обе переменные принимают значение 0.

Легко видеть, что дизъюнкция описывает работу цепи с п параллельно соединенными контактами.

Контакты не всегда независимы друг от друга. Можно устроить их так, чтобы они замыкались и размыкались одновременно, либо так, чтобы один из них размыкался, когда другой замыкается, и наоборот. В первом случае контакты называются идентичными, во втором – инверсными. Идентичные контакты обозначают одинаково; контакт, инверсный контакту р, будем обозначать через . Если контакту р поставить в соответствие переменную X, то очевидно, что контакту будет соответствовать формула: Когда переменная X принимает значение 1 (контакт р замкнут), формула принимает значение 0 (контакт разомкнут), и наоборот.

Установленные соответствия дают возможность описать любую цепь с последовательно или параллельно соединенными контактами формулой логики высказываний. С другой стороны, любую формулу логики высказываний можно смоделировать в виде переключательной схемы.

2. Анализ, упрощение и синтез переключательных схем.

Чтобыизучить свойства переключательной схемы, выявить ее возможности и особенности, достаточно рассмотреть соответствующую этой схеме формулу. Так, например, схеме на рисунке соответствует формула .

x	y	z	F
1	1	1	1
1	1	0	0
1	0	1	1
1	0	0	1
0	1	1	1
0	1	0	1
0	0	1	0
0	0	0	0

Составим для этой формулы таблицу истинности. Из таблицы видно, что цепь замкнута в 5 возможных случаях из 10 возможных: когда замкнуты все три контакта, только р₁ и р₃, только р₁, только р₂ и р₃, толькор₂.

Произведя равносильные преобразования,

,видим, что один из идентичных переключателей, например, р₃, лишний.

Мы провели анализ данной схемы, который выявил условия, при которых цепь замкнута, и обнаружили возможность ее упрощения, т.е. замены схемой с теми же свойствами, но с меньшим числом контактов.

Советский математик О.Б. Лупанов установил, что любую схему, соответствующую формуле с п переменными, всегда можно упростить так, что число контактов в ней не превысит .

Решим теперь такую задачу: построить цепь с тремя независимыми контактами, которая проводит ток тогда и только тогда, когда замкнуты ровно два контакта. Формула F(x, y, z), соответствующая искомой схеме, принимает значение 1 тогда и только тогда, когда это значение принимают две из трех переменных x, y, z. Напишем СДНФ формулы F: .Построим схему, соответствующую этой формуле (рис.).

В задаче использован общий метод построения (синтеза) переключательной схемы по заданным ее свойствам.

Вопросы для контроля:

1. Понятие переключательной схемы.

2. Анализ переключательных схем с помощью формул алгебры высказываний.

3. Упрощение переключательных схем.