
- •Раздел 1. Высказывания и операции над ними. Формулы алгебры высказываний. Классификация формул
- •1.1. Высказывания и операции над высказываниями
- •1.2. Формулы алгебры высказываний
- •1.3.Классификация формул
- •1.4. Значение тавтологий
- •1.5.Основные правила получения тавтологий
- •Раздел 2. Логическая равносильность формул
- •2.1. Отношение равносильности
- •2.2 Законы логики
- •2.3. Упрощение формул.
- •2.4. Равносильные преобразования. Упрощение формул
- •Раздел 3. Нормальные формы для формул алгебры высказываний
- •3.1 Нормальные формы
- •3.2 Совершенные нормальные формы
- •3.4 Получение скнф и сднф с помощью таблиц истинности
- •Раздел 4. Логическое следование
- •4.1 Логическое следование
- •Раздел 5. Применение алгебры высказываний в логико - математической практике
- •5.1 Получение следствий из данных посылок.
- •5.2. Получение следствий, содержащих заданные переменные.
- •5.3. Решение логических задач методом рассуждений.
- •5.4.Методы решение логических задач
- •Раздел 6. Исчисление высказываний.
- •6.1. Понятие переключательной схемы.
- •Раздел 7. Логика предикатов.
- •7.1. Понятие предиката
- •7.2. Способа задания предиката
- •7.3. Множество истинности предикатов
- •7.4. Язык логики предикатов
- •7.5. Следование и включение
- •7.6. Понятие отношений. Свойства отношений.
- •Раздел 8. Исчисление предикатов
- •8.1.Кванторы общности и существования
- •8.2. Квантификация многоместной высказывательной формы.
- •8.3. Отрицание предложений кванторами.
- •8.4. Численные кванторы
- •8.5. Символическая запись определений и теорем.
- •Раздел 9. Алгоритмы. Свойства алгоритмов.
- •9.1 Интуитивное понятие алгоритма.
- •9.2 Свойства алгоритмов
- •Раздел 10. Основная формализация (Машина Поста и мнр).
- •10.1 Машина Поста
- •10.2 Уточнение понятия алгоритма
- •Раздел 11. Основные формализации (мт и на)
- •11.1 Машина Тьюринга (мт)
- •11.2 Нормальные алгоритмы Маркова
- •11.3 Механизм работы нам:
2.2 Законы логики
Равносильности формул логики высказываний часто называют законами логики. Перечислим наиболее важные из них:
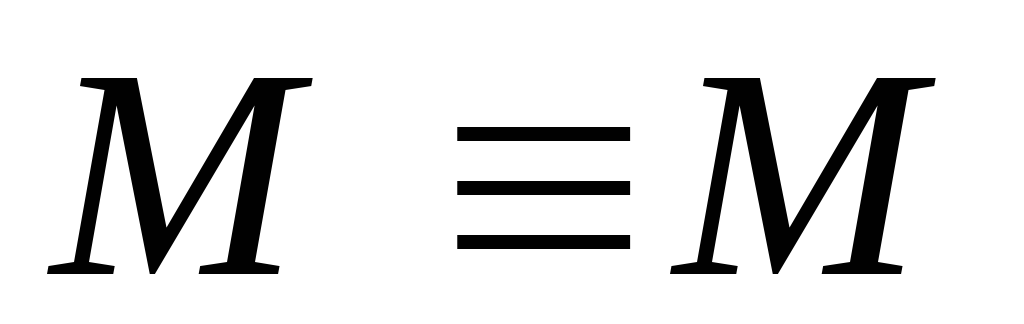 –закон
тождества.
–закон
тождества.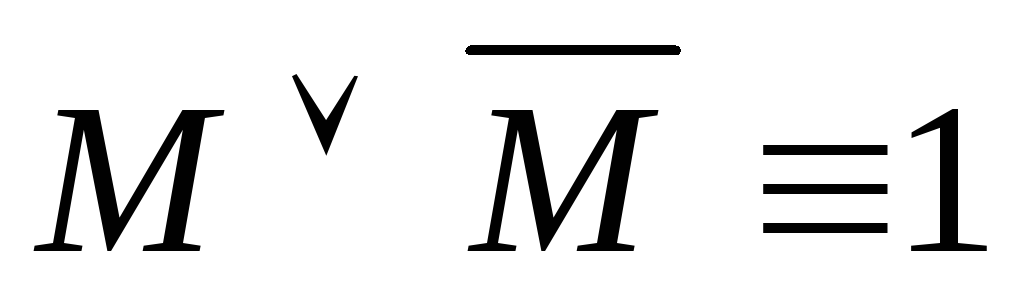 –закон
исключенного третьего
–закон
исключенного третьего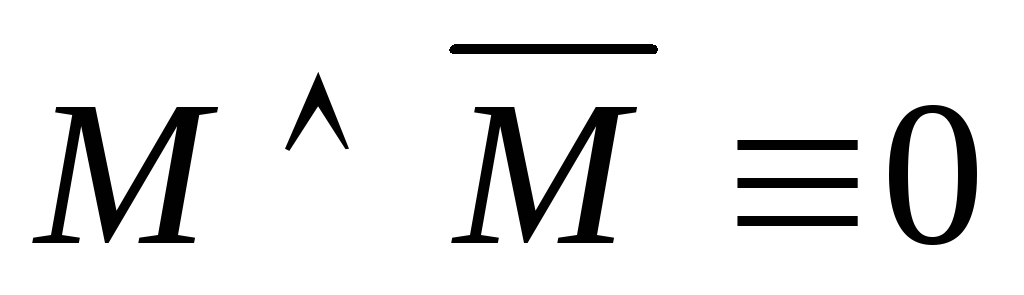 –закон
противоречия
–закон
противоречия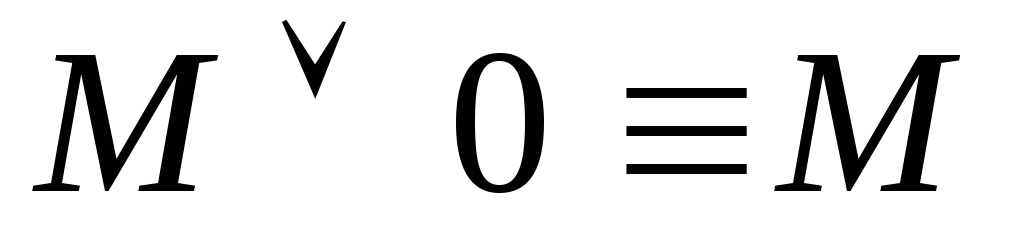
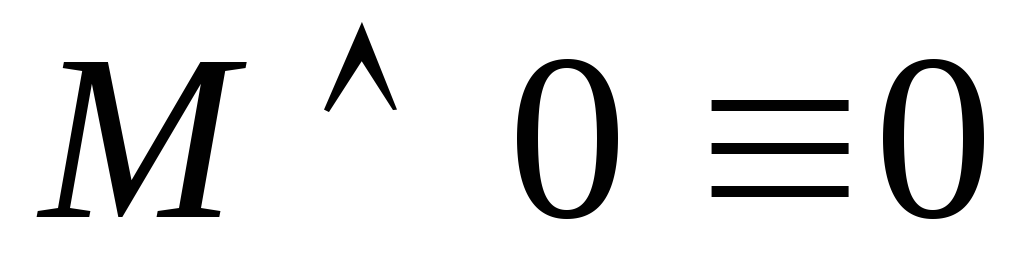
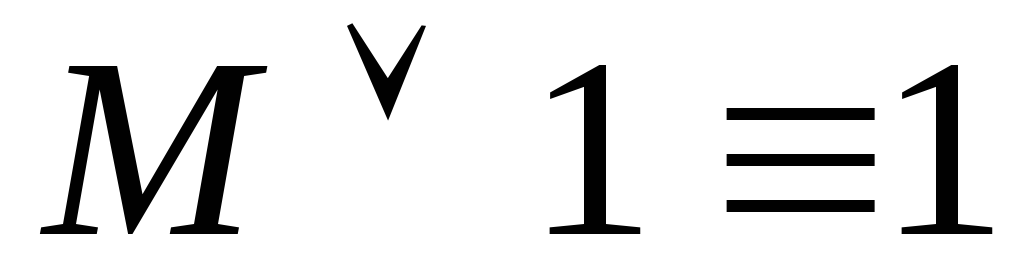

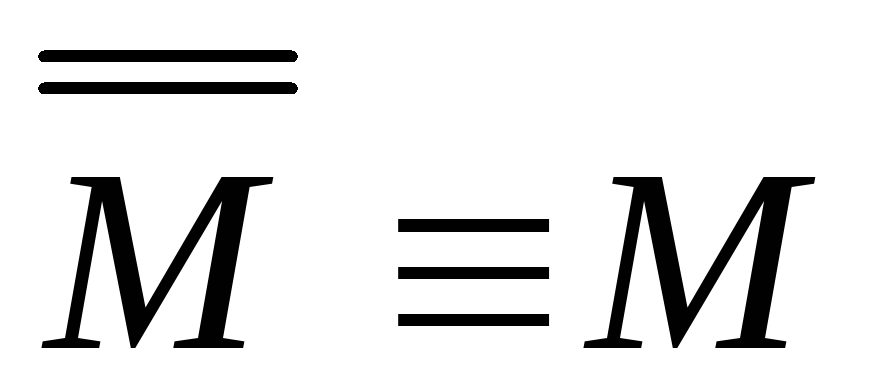 –закон
двойного отрицания
–закон
двойного отрицания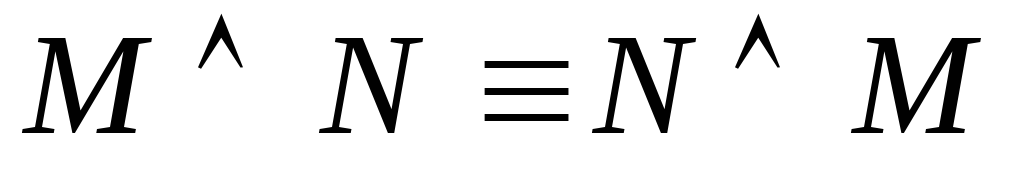 –коммутативность
конъюнкции
–коммутативность
конъюнкции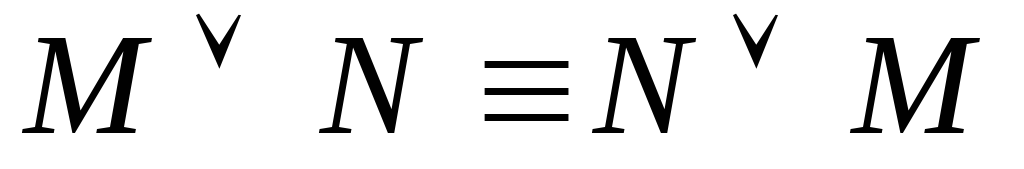 –коммутативность
дизъюнкции
–коммутативность
дизъюнкции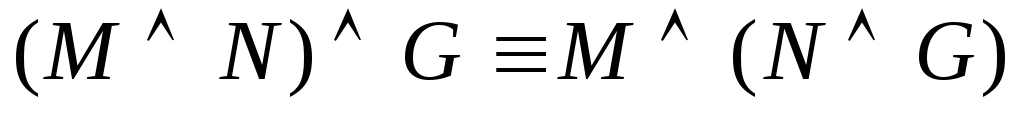 –ассоциативность
конъюнкции
–ассоциативность
конъюнкции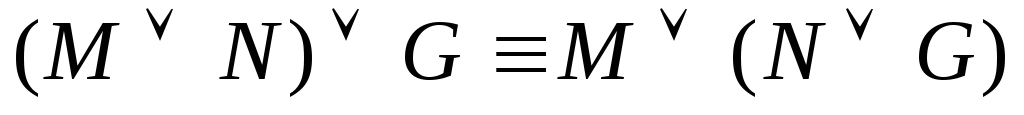 –ассоциативность
дизъюнкции
–ассоциативность
дизъюнкции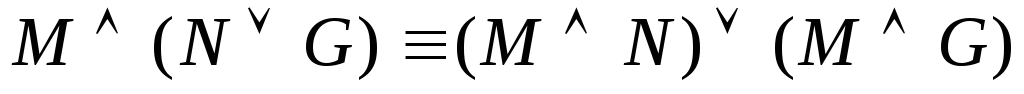 –дистрибутивность
конъюнкции
–дистрибутивность
конъюнкции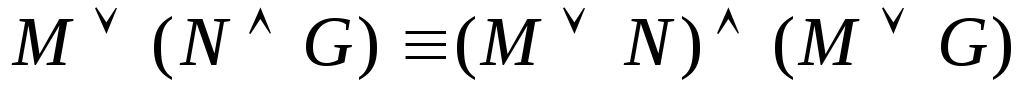 –дистрибутивность
дизъюнкции
–дистрибутивность
дизъюнкции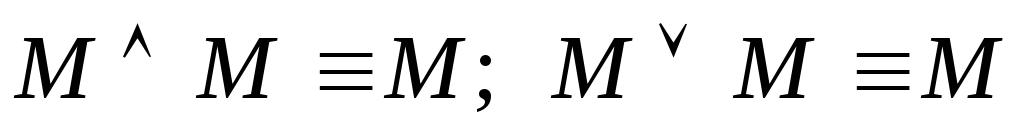 –законы
идемпотентности
–законы
идемпотентности ;
;
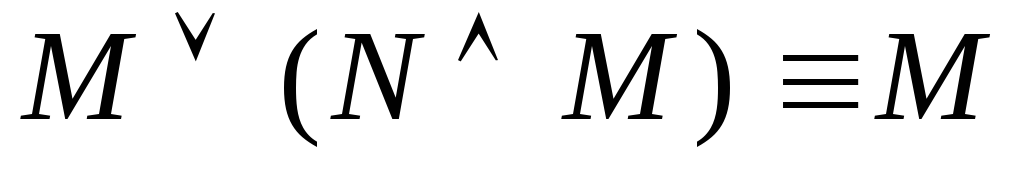 – законы поглощения
– законы поглощения ;
;
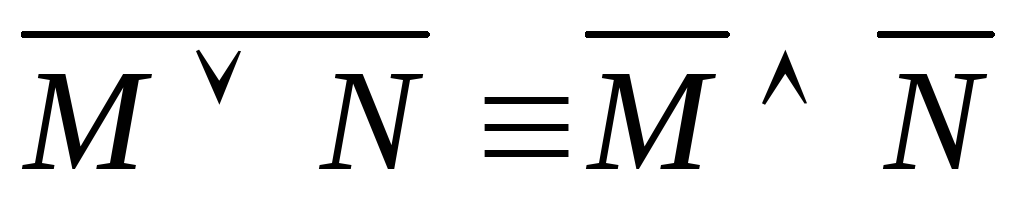 – законы де Моргана
– законы де Моргана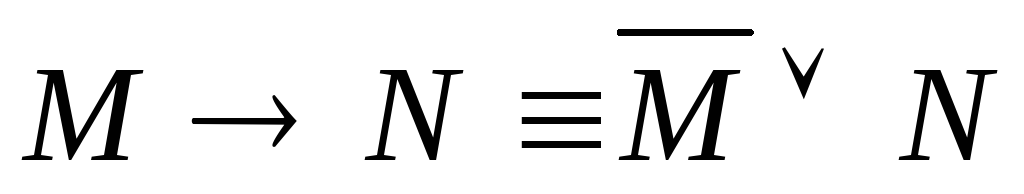 –закон,
выражающий импликацию через дизъюнкцию
–закон,
выражающий импликацию через дизъюнкцию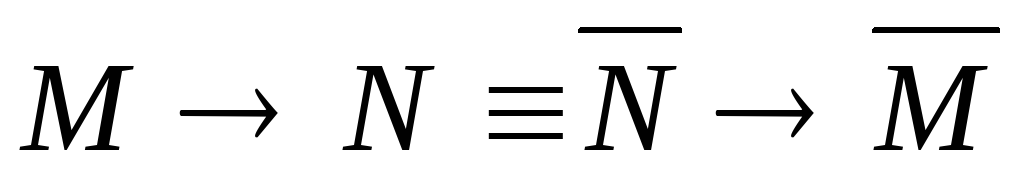 –закон
контрапозиции
–закон
контрапозиции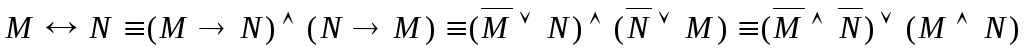 –законы,
выражающие эквиваленцию через другие
логические операции
–законы,
выражающие эквиваленцию через другие
логические операции
Законы логики используются для упрощения сложных формул и для доказательства тождественной истинности или ложности формул.
2.3. Упрощение формул.
Пример 1. Упростить формулу (АvВ) ^ (АvС) Решение.а) Раскроем скобки ( A vB ) ^ ( A v C ) ^ v ^C v B^A v B^C б) По закону идемпотентности A^A , следовательно, ^ v ^C v B^A v B^C v ^C v B^A v B^C в) В высказываниях А и А· C вынесем за скобки А и используя свойство Аv1 1, получим АvА^Сv ^ v ^C ( ^ v С v ^ v ^С v ^ v ^С
Аналогично пункту в) вынесем за скобки высказывание А. v^ v ^С ^ v ^С v ^С Таким образом, мы доказали закон дистрибутивности.
Пример 2. Упростить выражение v ^
Решение. v ^ v - поглощение
Пример
3.
Упростить выражение ^
v
^
![]() Решение.
^
v
^
Решение.
^
v
^
![]()
v
v
![]()
- склеивание
- склеивание
Всякую
формулу можно преобразовать так, что в
ней не будет отрицаний сложных высказываний
- все отрицания будут применяться только
к простым высказываниям.
Пример
4.
Преобразовать
формулу![]() так, чтобы не было отрицаний сложных
высказываний. Примечание!!!!
знак
«+» - дизъюнкция; знак «∙»-конъюнкция.
так, чтобы не было отрицаний сложных
высказываний. Примечание!!!!
знак
«+» - дизъюнкция; знак «∙»-конъюнкция.
Решение.1.
Воспользуемся формулой де Моргана,
получим:
![]()
![]() 2.
Для выражения
2.
Для выражения
![]() применим
еще раз формулу де Моргана, получим:
применим
еще раз формулу де Моргана, получим:
![]()
Любую формулу можно тождественно преобразовать так, что в ней не будут использованы: - знаки логического сложения; - знаки логического умножения. - знаки отрицания и логического умножения; - знаки отрицания и логического сложения.
Пример
5.
Преобразовать формулу
![]() так,
чтобы в ней не использовались знаки
логического сложения.
Решение.
Воспользуемся законом двойного отрицания,
а затем формулой де Моргана.
так,
чтобы в ней не использовались знаки
логического сложения.
Решение.
Воспользуемся законом двойного отрицания,
а затем формулой де Моргана.
![]()
Пример
6.
Преобразовать формулу![]() так, чтобы в ней не использовались знаки
логического умножения.
Решение.
Используя формулы де Моргана и закон
двойного отрицания получим:
так, чтобы в ней не использовались знаки
логического умножения.
Решение.
Используя формулы де Моргана и закон
двойного отрицания получим:
![]()
Эквиваленция выражается через конъюнкцию и импликацию:
Из
(3) и (1) получаем:
![]()
![]()
![]()
![]()
Y
Y![]()
![]()
X
X
![]()
![]()
(4)
Эта равносильность выражает
эквиваленцию через конъюнкцию, дизъюнкцию
и отрицание.
Из равносильностей (3) и
(2) получаем равносильность:
=
(4)
Эта равносильность выражает
эквиваленцию через конъюнкцию, дизъюнкцию
и отрицание.
Из равносильностей (3) и
(2) получаем равносильность:
=![]()
![]() (5),
выражающую
эквиваленцию через конъюнкцию и
отрицание.
(5),
выражающую
эквиваленцию через конъюнкцию и
отрицание.
2.4. Равносильные преобразования. Упрощение формул
Если в равносильные формулы всюду вместо какой-нибудь переменной подставить одну и ту же формулу, то вновь полученные формулы также окажутся равносильными в соответствии с правилом подстановки. Таким способом из каждой равносильности можно получить сколько угодно новых равносильностей.
Пример
1: Если
в законе де Моргана
![]() вместоХ
подставить
вместоХ
подставить
![]() ,
а вместоY
подставить
,
а вместоY
подставить
![]() ,
то получим новую равносильность
,
то получим новую равносильность![]() .
Справедливость полученной равносильности
легко проверить с помощью таблицы
истинности.
.
Справедливость полученной равносильности
легко проверить с помощью таблицы
истинности.
Если
какую-нибудь формулу
![]() ,
являющуюся частью формулыF,
заменить формулой
,
являющуюся частью формулыF,
заменить формулой
![]() ,
равносильной формуле
,
равносильной формуле![]() ,
то полученная формула окажется
равносильной формулеF.
,
то полученная формула окажется
равносильной формулеF.
Тогда для формулы из примера 2 можно провести следующие замены:
![]() –закон
двойного отрицания;
–закон
двойного отрицания;
![]() –закон
де Моргана;
–закон
де Моргана;
![]() –закон
двойного отрицания;
–закон
двойного отрицания;
![]() –закон
ассоциативности;
–закон
ассоциативности;
![]() –закон
идемпотентности.
–закон
идемпотентности.
По
свойству транзитивности отношения
равносильности можем утверждать, что
![]() .
.
Замену одной формулы другой, ей равносильной, называют равносильным преобразованием формулы.
Под упрощением формулы, не содержащей знаков импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая не содержит отрицаний неэлементарных формул (в частности, двойных отрицаний) или содержит в совокупности меньшее число знаков конъюнкции и дизъюнкции, чем исходная.
Пример
2:
Упростим формулу
![]() .
.
![]() .
.
На первом шаге мы применили закон, преобразующий импликацию в дизъюнкцию. На втором шаге применили коммутативный закон. На третьем шаге применили закон идемпотентности. На четвертом – закон де Моргана. И на пятом – закон двойного отрицания.
Замечание 1. Если некоторая формула является тавтологией, то и всякая равносильная ей формула также является тавтологией.
Таким образом, равносильные преобразования можно также применять для доказательства тождественной истинности тех или иных формул. Для этого данную формулу нужно равносильными преобразованиями привести к одной из формул, которые являются тавтологиями.
Замечание 2. Некоторые тавтологии и равносильности объединены в пары (закон противоречия и закон альтернативы, коммутативный, ассоциативный законы и т.д.). В этих соответствиях проявляется так называемый принцип двойственности.
Две
формулы, не содержащие знаков импликации
и эквиваленции, называются двойственными,
если каждую из них можно получить из
другой заменой знаков
![]() соответственно на
соответственно на![]() .
.
Принцип двойственности утверждает следующее:
Теорема 2.2: Если две формулы, не содержащие знаков импликации и эквиваленции, равносильны, то и двойственные им формулы также равносильны.
Вопросы для контроля:
Равносильные предложения. Равносильные формулы.
Свойства отношения равносильности.
Равносильные преобразования.
Упрощение формул.
Применение равносильных преобразований.
Принцип двойственности.
