
- •Глава II. Элементы векторной алгебры и аналитической геометрии
- •§1. Система координат
- •1.1 Система координат на плоскости (пространство r2 )
- •1.2 Простейшие задачи аналитической геометрии Расстояние между двумя точками на плоскости
- •Деление отрезка в данном отношении
- •§2 Векторы.
- •1.Основные понятия
- •2. Линейные операции с векторами Сложение векторов
- •Вычитание
- •Умножение вектора на число
- •3. Проекция вектора на ось
- •4.Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
- •Обозначим проекции на координатные оси, через.
- •5. Действия над векторами в координатной форме
- •§3. N- мерное векторное пространство. Линейная зависимость и независимость векторов.
- •§4. Скалярное, векторное и смешанное произведения векторов
- •4.1 Скалярное произведение, его свойства и вычисление
- •Механический смысл скалярного произведения
- •Геометрический смысл векторного произведения
- •Механический смысл векторного произведения
- •Свойства векторного произведения
- •Векторное произведение векторов, заданных координатами
- •4.3 Смешанное (векторно-скалярное) произведение векторов, его геометрический смысл
- •Свойства смешанного произведения
- •Смешанное произведение векторов, заданных координатами
§4. Скалярное, векторное и смешанное произведения векторов
4.1 Скалярное произведение, его свойства и вычисление
Опр.1Скалярным произведением векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Обозначается
скалярное произведение
![]() или
или
![]() или
или
![]() =
=![]() (4.1)
(4.1)
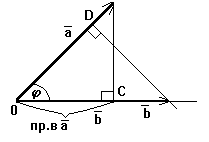 Рис.
1
Рис.
1
OC=![]() ,OD=
,OD=![]() .
.
Если
учесть, что в формуле (4.1) произведение
![]() равно проекции вектора
равно проекции вектора![]() на ось вектора
на ось вектора![]() ,
получим:
,
получим:
![]() .
.
Аналогично
![]() – есть проекция
– есть проекция![]() на ось вектора
на ось вектора![]() ,
т.е.
,
т.е.
![]() .
.
Учитывая сказанное, получим 2-е определение скалярного произведения.
Опр.2 Скалярное произведение векторов равно произведению
модуля одного из них на проекцию на него же второго
вектора.
![]() (4.2)
(4.2)
(определение скалярного произведения через проекции).
Формула (4.1) так же как и (4.2) часто используется при решении задач
Механический смысл скалярного произведения
В механике часто приходится вычислять работу, совершаемую переменной силой, если точка её приложения перемещается по прямой.
Если
сила f
перемещается по вектору
![]() (от начала к концу), то работа, производимая
этой силой, равна скалярному произведению
силыf
на вектор
(от начала к концу), то работа, производимая
этой силой, равна скалярному произведению
силыf
на вектор
![]() :
:
![]() .
(4.3)
.
(4.3)
Свойства скалярного произведения
Относительно скалярного произведения имеют место следующие законы:
10 ![]() (коммутативный
или переместительный закон);
(коммутативный
или переместительный закон);
20 ![]() (ассоциативный или
(ассоциативный или
сочетательный закон);
30 ![]() (дистрибутивный
или
(дистрибутивный
или
распределительный закон);
40 ![]() ;
;
50 ![]() ,
если
,
если![]() и обратно: если
и обратно: если![]()
![]()
Скалярное произведение в координатах
Если
два вектора заданы в координатах
![]() и
и![]() ,
то скалярное произведение их равно
сумме произведений одноимённых координат:
,
то скалярное произведение их равно
сумме произведений одноимённых координат:
![]() .
(4.4)
.
(4.4)
Необходимым и достаточным условием перпендикулярности двух векторов является равенство:
![]() .
(4.5)
.
(4.5)
Угол между векторами вычисляется по формуле:
![]() .
(4.6)
.
(4.6)
71
4.2 Векторное произведение векторов
Опр.
3 Векторным
произведением
векторов
![]() и
и
![]() называется
называется
вектор
![]() ,
который удовлетворяет трём условиям:
,
который удовлетворяет трём условиям:
1.Он
перпендикулярен к перемножаемым векторам
![]() ;
;
2.Длина его (модуль) равна произведению модулей перемножаемых векторов на синус угла между ними:
![]() ;
(4.7)
;
(4.7)
Направлен он таким образом, что если посмотреть из его конца, то кратчайший поворот первого перемножаемого вектора ко второму должен быть виден против хода часовой стрелки.
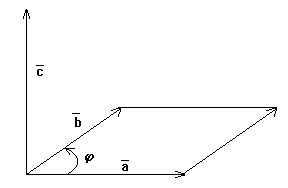 Рис.
2
Рис.
2
Обозначается векторное произведение:
![]() или
или
![]() .
.
Геометрический смысл векторного произведения
Из определения векторного произведения видно, что модуль его численно равен площади параллелограмма, построенного на этих векторах, как на составляющих, т.е.
![]() (рисунок 2).
(рисунок 2).
Так
как
![]() , то
, то![]() .
(4.8)
.
(4.8)
Механический смысл векторного произведения
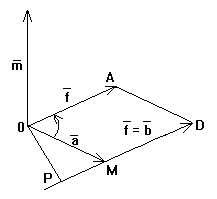 Рис.
19
Рис.
19
Пусть
заданы две точки О и М. Пусть сила
приложена к т. М и равна вектору
![]() ,
а из точки О в т. М идёт вектор
,
а из точки О в т. М идёт вектор![]() ,
(т.е.
,
(т.е.![]() ).
).
Тогда
моментом силы f
относительно точки
![]() называется векторное произведение
векторов
называется векторное произведение
векторов![]() и
и![]() ,
т.е. вектор
,
т.е. вектор![]() ,
равный:
,
равный:
![]() ,
(4.9)
,
(4.9)
так
как
![]() (рисунок 19).
(рисунок 19).
Вектор
![]() (момент
силы
(момент
силы![]() )
перпендикулярен к векторам
)
перпендикулярен к векторам![]() и
и![]() ,
имеет длину, равную площади параллелограмма,
построенного на векторах
,
имеет длину, равную площади параллелограмма,
построенного на векторах![]() и
и![]() .
.
Если
из точки
![]() опустить перпендикуляр на вектор
опустить перпендикуляр на вектор![]() ,
то
,
то![]() -
есть плечо силы
-
есть плечо силы![]() ,
т.е. модуль момента равен произведению
модуля силы
,
т.е. модуль момента равен произведению
модуля силы![]() на плечо
на плечо
![]() (рисунок
19),
(рисунок
19),
где
OP
- высота параллелограмма
![]() ,
,![]() -
длина основания.
-
длина основания.
