1. Краткий обзор систем обучения

В методических публикациях последнего двадцатилетия часто встречаются слова «традиционная система», «альтернативная сис­тема» обучения. Эти названия легко понимаются педагогами, работавшими в школе в 1980—1990 гг., но они не всегда понятны сегодняшним студентам и молодым учителям. Поясним происхо­ждение и смысл этих названий.

В Советском Союзе была принята жесткая цензура школьных учебников. Учителям разрешалось работать только по тем учебни­кам, которые были утверждены и рекомендованы Министерством образования. По каждому предмету для начальной школы Мини­стерством образования утверждался только один учебник. В 1968 г. был объявлен конкурс на написание учебника по математике для начальной школы. Из всех предложенных учебников был выбран и утвержден в качестве единого учебник, написанный авторским коллективом под руководством М.А. Байтовой и М.И. Моро. Этот учебник, в дальнейшем незначительно перерабатываясь, выдержал более 20 изданий, его стали называть традиционным. Долгие годы он был единственным для обучения математике в начальной школе.

Подобная политика позволяла создать единое образовательное пространство на всей территории бывшего Советского Союза, учились по одному и тому же учебнику и по единому учебному плану. С одной стороны, это было удобно, поскольку не возникало проблем в связи с переездами и сменой школы. Но, с другой сторо­ны, эта система приводила к жесткой унификации образователь­ного процесса, при которой учитель был ориентирован главным образом на достижение каждым ребенком определенного уровня учебных норм и требований. Сегодня эту ориентацию называют «знаниевой парадигмой».

После развала Советского Союза стали публиковаться учебни­ки других авторов, эти учебники стали называть «альтернативны­ми». Некоторые из них были написаны еще в 70-е годы XX в. (учеб­ники системы Л.В. Занкова, системы В.В. Давыдова и др.), другие изданы в 90-е годы (учебники Н.Я. Виленкина и Л.Г. Петерсон, учебники Н.Б. Истоминой и др.).

A.M. Пышкало отмечает, что традиционный курс математики для начальных классов характеризуется определенной последова­тельностью изучаемых базисных понятий: Число —> Величина. Этот же подход, как и традиционная программа обучения, используется в школах (классах) V вида.

Лекция 4. Психолого-педагогические основы организации математического развития младших школьников

Рассмотрим различные подходы к определению понятия «ма­тематическое развитие» ребенка. Анализ литературы показывает, что авторы по-разному понимают этот термин. В основном имеют место две трактовки этого понятия.

В первом случае «математическое развитие» ассоциируется с по­нятием «математические способности», которые имеют природный характер. В этом случае успешность ребенка в освоении матема­тического содержания связывается педагогами с наличием этих природных способностей и отрицанием возможности методически влиять на них. Как следствие на практике часто наблюдается ори­ентация педагогов более на природные данные ребенка, чем на по­иск и применение методик организации математического разви­тия ребенка, обладающего слабыми природными способностями к математике.

Во втором случае под «математическим развитием» понимают формирование и накопление математических знаний и умений у ребенка. Предполагается, что развитие умственных способностей при этом достигается косвенным путем: в процессе усвоения зна­ний. Таким образом, математическое развитие рассматривается как следствие обучения математическим знаниям. Если бы данный подход к математическому развитию ребенка был верным, то дос­таточно было бы отобрать круг знаний, сообщаемых ребенку, и по­добрать соответствующий метод обучения, чтобы сделать этот про­цесс продуктивным, т. е. получать в результате высокое матема­тическое развитие у всех детей. Данный подход в значительной мере пытались реализовать при создании различных альтернатив­ных учебников математики для начальной школы (Л.В. Занков, В. В. Давыдов, Н.Я. Виленкин, A.M. Пышкало и др.), наполняя эти учебники различным содержанием: увеличивали долю арифме­тического материала, долю алгебраического материала, вводили элементы теории множеств, комбинаторики, алгоритмики и др.. Ап­робации этих учебников на протяжении более 40 лет показала, что заметного влияния на уровень математического развития младших школьников эти системы не оказывают. При этом очевидно, что говорить об отсутствии влияния содержания обучения на разви­тие как математического мышления, так и общего развития мыш­ления ребенка неправомочно.

В исследованиях Д. Б. Эльконина и В. В. Давыдова было достаточно убедительно доказано, что проблема обновления содержания обучения в начальных классах является частью проблемы организа­ции развивающего обучения ребенка младшего школьного возра­ста. Психологическое обоснование важности и особой значимости этой проблемы было разработано Д. Б. Элькониным (1960, 1966) и В.В. Давыдовым (1966, 1972), в исследованиях которых было деталь­но показано, что одним из решающих факторов в развитии мышления младших школьников выступает содержание обучения. Известный советский кибернетик А.А. Фельдбаум отмечал: «Накопление зна­ний играет в процессе обучения немалую, но отнюдь не решающую роль. Человек может забыть многие конкретные факты, на базе кото­рых совершенствовались его качества. Но если они достигли высо­кого уровня, то человек справится со сложнейшими задачами, а это и означает, что он достиг высокого уровня культуры»¹ (т. е. мышле­ния). Таким образом, связь между содержанием обучения и процессом развития мышления ребенка, несомненно, существует, но ее нельзя считать достаточным условием обеспечения математического раз­вития ребенка. В то же время психологически и дидактически обос­нованный отбор этого содержания, несомненно, будет играть зна­чительную роль в процессе создания управляемой системы матема­тического развития ребенка.

Под математическим развитием ребенка младшего школьного возраста будем понимать целенаправленное и методически орга­низованное формирование и развитие совокупности взаимосвя­занных основных (базовых) свойств и качеств математического мышления ребенка и его способностей к математическому по­знанию действительности. Такое развитие задает главную целевую установку обучения математике детей младшего возраста.

Методическая система (включая технологию) непрерывного мате­матического развития ребенка младшего возраста, предоставляющая каждому ребенку условия для индивидуального продвижения в ма­тематическом содержании (траектории) будет способствовать:

- практическому созданию единой системы преемственного до­школьного и начального обучения математике;

- достижению оптимально возможного для ребенка, соответст­вующего возрастному этапу уровня математического развития.

Таким образом, понятие «математическое раз­витие» ребенка дошкольного и младшего школьного возраста не следует полностью ассоциировать с понятием «математические способности» (природного характера). Успешность ребенка в ос­воении математического содержания во многих случаях связана с наличием этих природных способностей, но организация мате­матического развития ребенка, обладающего слабыми природны­ми способностями к математике, вполне возможна при условии применения соответствующих методик. При этом в одних случаях процесс целенаправленного математического развития ребенка бу­дет приводить к дальнейшему развитию природных математиче­ских способностей, в других случаях — к оптимальному развитию необходимых для успешного усвоения математического содержа­ния свойств и качеств мышления, в третьих случаях — к коррек­ции недостатков познавательного развития ребенка и создании предпосылок для более успешного усвоения математического со­ держания при дальнейшем обучении.

Целенаправленная работа по организации математического раз­вития ребенка младшего школьного возраста будет способствовать общему повышению уровня развития интеллектуальных (умствен­ных) способностей каждого ребенка, что в свою очередь благопри­ятно отразится на успешности обучения детей предметному содер­жанию. Эта работа будет также способствовать личностному раз­витию ребенка, поскольку такие качества математического стиля мышления как целеустремленность, критичность, широта, гиб­кость, организованность, логичность и др. являются в то же время личностными характеристиками качеств ума и характера человека.

Итак, цель математического развития ребенка младшего школь­ного возраста — это стимуляция и развитие математического мыш­ления (соответствующих возрасту компонентов и качеств этого мышления).

Психолого-дидактическим обоснованием этого подхода являет­ся своеобразие возрастного развития познавательных и когнитив­ных процессов ребенка младшего возраста, обусловленное тем, что в возрасте 3—5 лет ведущим типом мышления ребенка является наглядно-действенный тип, а в возрасте 6—10 лет — наглядно-об­разный тип мышления. Возраст 10—12 лет является переходным к ведущему абстрактному (словесно-логическому) типу мышления.

Это обусловливает необходимость использования для организа­ции математического развития ребенка на каждом из обозначен­ных этапов соответствующего содержания и методологии, макси­мально соответствующих «детскому способу» вхождения в математику оптимально возрасту ребенка. Опора на ведущий тип мышления ребенка дает основание сделать вывод: главным направ­лением организации математического развития ребенка дошколь­ного возраста является целенаправленное развитие конструктив­ного мышления, а ребенка младшего школьного возраста — разви­тие пространственного мышления. Эти виды математического мышления сенситивны указанным возрастам, и потому наиболее чувствительны к методическому развивающему воздействию педа­гога. Таким образом, наиболее способствующей математическому развитию ребенка младшего школьного возраста будет та система обучения математике (и, соответственно, те учебники), которая в 1 классе (6 лет) предусматривает специальную методическую работу по развитию конструктивного мышления ребенка, а во 2—4 классах — специальную работу по развитию пространствен­ного мышления в сочетании с активной пропедевтикой основ сло­весно-логического мышления.

Методологическим обоснованием предлагаемой концепции явля­ется выбор в качестве ведущего метода обучения детей математиче­скому содержанию метода моделирования, с преимущественным использованием на каждом возрастном этапе того вида моделирова­ния, который более всего соответствует возрастным особенностям развития мышления и других познавательных процессов. В возрасте 3—5 лет — это конструирование (вещественное моделирование); в возрасте 6—10 лет — сочетание конструирования с графическим моделированием (с постепенным перенесением акцента на послед­нее), в возрасте 10—12 лет — графическое моделирование с элемента­ми конструирования (там, где необходимо практическое приложение знаний и умений ребенка в математике), и с элементами логико-сим­волического моделирования (знакового и символьного) в качестве подготовки к переходу ребенка на ведущий словесно-логический (аб­страктный) тип мышления в старшем возрасте. Такой подход к вы­бору ведущего метода обучения обеспечивает эффективное развитие приемов умственной деятельности у ребенка (анализа, синтеза, абст­рагирования, обобщения и др.), развитие практико-ориентированной интуиции в применении математических знаний, самостоятельности в учебно-познавательной деятельности и таких качеств математичес­кого мышления как гибкость, критичность, активность, целенаправ­ленность и др.

Модель изучаемого математического понятия или отноше­ния играет роль универсального средства изучения свойств математических объектов. При таком подходе к формированию на­чальных математических представлений не только учитывает­ся специфика математики (науки, изучающей количественные и пространственные характеристики реальных объектов и процес­сов), но и происходит обучение ребенка общим способам деятель­ности с математическими моделями реальной действительности и способам построения этих моделей.

Являясь общим приемом изучения действительности, модели­рование позволяет эффективно формировать такие приемы умст­венной деятельности как классификация, сравнение, анализ и син­тез, обобщение, абстрагирование, индуктивные и дедуктивные способы рассуждений, что в свою очередь стимулирует в перспек­тиве интенсивное развитие словесно-логического мышления. Таким образом, можно считать, что данный подход будет обеспе­чивать формирование и развитие математического мышления ребенка, а, следовательно, будет обеспечивать его математическое развитие.

Лекция 5. Теоретические основы преподавания математики в пропедевтический период

Определяя учебный предмет и задачи методики обучения этому предмету, считается, что методика дает ответы на вопросы: чему следует учить и как лучше это сделать (с помощью каких методов, средств, форм организации учебных занятий). На современном этапе развития педагогической системы эти вопросы уточнены и систематизированы.

Методическую систему обучения математике можно изобразить в виде схемы.

		Цели обучения
Содержание обучения				Методы обучения

Средства обучения

Формы организации

Схема 1. Методическая система обучения математике

В этой схеме обозначены связи, существующие между элементами методической системы. Понимание и учет этих связей во многом определяют уровень методического мастерства учителя и возможность творческого решения возникающих в практике вопросов.

Поскольку основным элементом методической системы являются цели обучения, то остановимся на их характеристике. В начальных классах школы дети должны сознательно и прочно овладеть определенным кругом знаний, умений, навыков в области математики.

Одной из важных задач начального обучения является формирование сознательных и прочных навыков вычислений. В объяснительной записке к программе указывается, что начальный курс математики предполагает изучение свойств действий, существующих между ними связей, математических отношений и зависимостей, являющихся основой формируемых у детей практических навыков и умений. Цели обучения в современной школе предполагают не только усвоение ряда предусмотренных программой фактов и правил, но и овладение умением самостоятельно применять приобретенные знания к решению разнообразных учебных и практических задач.

В начальном курсе математики предусматривается постепенная подготовка учащихся к усвоению понятий, например, переменной (термин в начальных классах не используется). Начинается эта работа в 1 классе, где рассматривается примеры «с окошечком»: 6+*=10, *+*=7, 5>*, 3<*. В начальных классах дети встречаются и с простейшими уравнениями, где буква обозначает пока лишь определенное неизвестное число. При ознакомлении с геометрическим материалом значительное место уделяется измерениям. Дети должны научиться находить длину отрезка. Формированию элементарных навыков черчения уделяется специальное внимание. Дети должны научиться пользоваться линейкой, угольником. Это и вычерчивание отрезков заданной длины, и измерение отрезка с помощью мерной линейки, и построение на клетчатой бумаге прямоугольника, квадрата. Начиная уже с первого класса, решаются простые и составные текстовые задачи, поскольку трудно переоценить роль текстовых задач при ознакомлении детей со связью, существующей между такими величинами, как, например, цена, количество и стоимость, время, скорость и расстояние и т.п.

Основным элементом в оснащении учебного процесса при обучении математике является учебник. Он строится в полном соответствии с программой. Учебник уточняет, конкретизирует, детализирует требования программы в отношении содержания обучения математике в начальных классах школы.

Например, в программе для первого класса дается обобщенная формулировка: «Таблица сложения в пределах 10, соответствующие случаи состава чисел. Вычитание в пределах 10».

Система ознакомления учащихся с различными случаями сложения и вычитания в пределах 10 раскрывается в учебнике.

Успешное овладение математикой осуществляется в процессе выполнения упражнений. Методическую цель упражнения определяет главным образом его математическое содержание. Это содержание зависит от программы обучения в соответствующем классе. В зависимости от содержания материала задания математического характера в первом классе подразделяются на:

1. подготовительный этап;

2. изучение нумерации в пределах 10;

3. усвоение смысла арифметических действий и формирование вычислительных навыков;

4. знакомство с величинами и единицами их измерения;

5. знакомство с задачей.

Рассмотрим подробнее подготовительный этап. Данный этап необходим, чтобы подготовить учащихся к восприятию и усвоению математических понятий, связей между ними, для более успешного и продуктивного изучения математики. Учащиеся должны получить определенные умения и навыки.

Пропедевтическим этапом предусмотрены упражнения:

• на выделение признаков объекта;

• на выделение количественных характеристик множеств;

• на пространственное расположение предметов;

• на развитие познавательных процессов:

- мышление,

- память,

- внимание,

- восприятие,

- воображение;

• на развитие характерных качеств математического мышления:

- гибкость,

- причинность,

- системность,

- пространственная подвижность.

Задачами подготовительного периода в первом классе является повседневное изучение ребенка, наблюдение и изучение его психолого-педагогических особенностей, степень овладения жизненным опытом в дошкольный период.

В пропедевтический период уроки должны быть организованы таким образом, чтобы они способствовали пробуждению и привитию интереса к математике. Поэтому форма организации занятий не должна быть однородной. Желательно, чтобы в этот период проводились экскурсии, во время которых учащимся представлялся бы широкий материал по сравнению предметов по размерам, пространственному расположению, форме и т.д. Организуя экскурсии в школьные мастерские, на пришкольный участок, в парк.

При организации урока необходимо помнить о тесной связи преподавания математики с жизнью. Материал, который подбирается для урока, должен иметь для ребенка жизненно-практическое значение. Ученик должен понять, что знания, которые он получает на уроке, необходимы ему в игровой и практической деятельности, то есть необходимы в повседневной жизни.

Содержание первых уроков должно быть доступным для всех учеников, вызывать у них интерес и доставлять радость. Учитель выявляет, уточняет и формирует общеучебные умения, правила поведения в классе: умение видеть демонстрируемые предметы, картинки, слушать, правильно понимать и выполнять требования учителя, отвечать на вопросы, задавать вопросы, повторять задание учителя, правильно сидеть за партой, вставать, выходить из-за парты.

На этом этапе важно выявить, как ребенок воспринимает помощь учителя, проявляет ли он интерес к учебе, какой вид деятельности является для него ведущим.

В пропедевтический период выявляется имеющийся у учащихся запас дочисловых и числовых представлений: количественных, пространственных, временных, представлений о форме предмета, величине и размерах, а также умение считать (счет вербальный и конкретный), знание цифр и чисел, умение производить действия сложения и вычитания, решать простые задачи на нахождение суммы и разности (остатка).

При изучении состояния арифметических знаний учитель обращает внимание на общее развитие ребенка. Он устанавливает, насколько хорошо ребенок ориентируется в окружающей обстановке.

Наряду с установлением актуальных знаний выявляются и потенциальные возможности школьников, а затем учащиеся готовятся к изучению математических знаний.

Выявление представлений учащихся о размерах предметов, понимание ими существенных признаков предметов вначале следует провести без использования дидактического материала, применяя знакомые для учащихся предметы окружающей обстановки, например: «Кто больше: кошка или корова?», «Что длиннее: класс или коридор?» и т.д. Если учащиеся не дают положительных ответов, то можно предложить для выделения существенных признаков предметов сами эти конкретные предметы, например: мячи – большой и маленький, линейки – длинную и короткую, шарики - металлический и пластмассовый и т.д.

Учитель также выявляет, умеют ли ученики считать и в каких пределах. При этом он обращает внимание на то, соотносят ли ученики названия числительных с показом соответствующего количества конкретных предметов. Учителем устанавливается также, может ли ученик начать счет с любого заданного числа и остановиться при счете в соответствии с заданием учителя («Посчитай от 3 до 7») или у него стереотипно заученный числовой ряд, который повторяется им независимо от требований учителя.

Проверяется, знают ли ученики цифры, могут ли назвать предъявляемые цифры по порядку и вразброс, могут ли соотнести цифру и число, а также цифру и то количество предметов, которое она обозначает, например: «Покажи цифру пять», «Сосчитай, сколько здесь матрешек, и положи нужную цифру», «Отсчитай столько карандашей, сколько показывает эта цифра».

Необходимо проверить знание геометрических фигур: умение отыскивать геометрическую фигуру по образцу (круг, квадрат, треугольник, прямоугольник), умение назвать фигуру, показать названную учителем фигуру, начертить фигуру, не имея ее образца.

Проверяется умение решать арифметические задачи на нахождение суммы и остатка в одно действие. Вначале предлагается решить задачу без пособий, а затем, если учащиеся с ней не справляются, конкретизировать предметами или рисунком.

Уроки математики в этот период должны быть оснащены достаточным количеством наглядных пособий и дидактического материала. Надо использовать красочный материал, настенные таблицы, иллюстративные наборные полотна.

Для более эффективной работы над учебным материалом необходимо применение различных средств наглядности. Основные функции наглядных пособий заключаются в том, чтобы помочь раскрыть содержание и объем новых понятий, закрепить изучаемый материал, быть средством контроля, обеспечить активную самостоятельную деятельность учащихся.

Наглядное обучение должно обеспечить формирование у учащихся первичных обобщений и установление простых связей. Оно должно способствовать движению мысли от жизненных наблюдений к сущности изучаемого понятия. В решении этих задач неоценимую помощь могут оказать различные виды учебного оборудования.

Самым распространенным видом наглядности является чертеж учителя на доске. Чертеж выполняется постепенно, в присутствии учащихся, этим объясняется высокая эффективность его воздействия в процессе обучения. Во время выполнения чертежа учащиеся получают возможность внимательно следить за объяснением учителя, пояснениями к чертежу. Заранее выполненный чертеж менее эффективен, хотя и требует меньших затрат времени. На уроках математики в начальной школе широко применяется пособия-аппликации (таблицы с подвижными и съемными деталями), магнитные доски, фланелеграф. Важное место на уроках занимают наборные полотна различной конструкции, изготовляемые из картона, фанеры, ткани, а также учебные таблицы. Среди технических средств обучения также применяются экранные средства.

Таким образом, наглядность, чувственное восприятие и практическая деятельность детей являются основой осознанного усвоения знаний, лучшим средством развития мышления детей.

В пропедевтический период учитель так строит урок, чтобы на нем выявить знания учащихся, их готовность к обучению математике и одновременно уточнять и формировать их представления о размерах предметов пространственные и количественные представления. Это возможно при условии тщательного планирования материала. Учитель ежедневно планирует, какие знания он должен проверить, какие знания дать, какие умения и навыки сформировать.

Анализ существующей литературы, а также специальные исследования показывают, что такими понятиями, как большой - маленький, учащиеся владеют. Из множества предметов они выделяют большие и маленькие предметы, однако не все учащиеся могут сравнивать предметы по размеру. Например, задание найти место матрешки в ряду матрешек, расставленных от меньшей к большей, или собрать башенку из колец, нанизывая кольца от большего к меньшему, оказывается доступным не всем учащимся, поступившим в 1-й класс.

Сравнение предметов по существенным признакам (длинный – короткий, высокий – низкий, широкий – узкий, толстый – тонкий) еще более затруднено. Во-первых, при определении признака предмета дети стараются заменить эти существенные признаки более общими: большой – маленький. Учащиеся оперируют словами высокий – низкий, длинный – короткий, широкий – узкий, но не имеют четкой, правильной дифференциации тех понятий, которые эти слова обозначают. Они часто заменяют одно понятие другим; например, вместо длинный говорят высокий, вместо тонкий – узкий, вместо широкий – толстый и т.д. Большинство учащихся, поступающих в 0 – 1–е классы не владеют приемами сравнения предметов. При сравнении предметов они стараются иногда накладывать предметы один на другой или прикладывать их друг к другу, но не знают, как выполнить наложение или приложение. Поэтому никакого сравнения не получается. Например, при сравнении двух лент по длине ученики не соединяют их концы, а короткую ленту прикладывают к середине длинной.

Целью уроков в подготовительный период является выявление, уточнение и развитие понятий о размерах, форме предметов, пространственных представлений учащихся, обогащение словаря учащихся новой терминологией, активизация пассивного словаря, развитие речи, активизация их познавательной деятельности, формирование общеучебных умений и навыков.

Таким образом, в пропедевтический период решается такая важная задача как подготовка учеников к обучению математике. От степени подготовленности зависит дальнейшее обучение, степень эффективности обучения. Такая подготовка осуществляется с помощью упражнений, средств наглядности, и, конечно, большая роль отводится умению учителя сформировать положительный настрой учащихся на изучение математики.

Лекция 6. Что понимается под трудностями в овладении арифметикой

Мы говорим о затруднениях в усвоении арифметики тогда, когда арифметические способности ученика не соответствуют возраст­ному уровню и тем возможностям, которые он демонстрирует по другим предметам. В соответствии с критериями Классификатора ВОЗ такие нарушения определяются как «нарушение арифмети­ческих действий, которое не связано с общим недоразвитием интеллекта ребенка, а появляется при неправильном обучении» (Диллинг и др., 1991). Имеется в виду, что арифметическая ком­петентность ребенка может быть ниже того уровня, который со­ответствует данному возрасту в данном классе при сохранном ин­теллекте.

У ребенка с таким нарушением страдают основные арифмети­ческие действия — сложение, вычитание, умножение и деление, что затрудняет освоение более сложных математических навыков, которых требуют занятия алгеброй, тригонометрией, геометрией. В данном случае имеются в виду частичные нарушения учебной деятельности, которые не мешают детям иметь успехи по другим предметам.

Однако есть дети, у которых возникают особые трудности со счетом. Эти отклонения сопровождаются общими трудностями в учебе, в частности страдает и чтение, и правописание, все это при среднем показателе IQ. Исследование Лобека (1992) показа­ло, что примерно у 16—18 % детей с трудностями в счете возни­кали проблемы и в чтении, 32 — 36% детей испытывали трудно­сти при написании диктанта. Примерно у 90 % этих детей показа­тель интеллекта составил 90, что свидетельствует об их нормаль­ном умственном развитии.

И, наконец, можно выделить группу детей, арифметические нарушения у которых объясняются общим низким уровнем обу­чаемости и соответственно сниженным уровнем интеллекта.

Все эти дети нуждаются в специальной помощи и поддержке. Все они имеют право на развитие.

Как при нарушениях в чтении и правописании, так и при на­рушениях в счете причины часто пытаются найти в особенностяхличности ребенка. Педагогическое мастерство, учебный материал и методы обучения не принимаются во внимание. Однако обуче­ние математике представляет собой процесс взаимодействия между ребенком, содержанием обучения и педагогом, и, следователь­но, нельзя связывать арифметические нарушения исключительно с особенностями изучаемого материала или особенностями лич­ности ребенка. Возникают следующие вопросы: какие способнос­ти необходимо иметь для овладения тем или иным учебным мате­риалом? В какой форме лучше всего преподносить данный мате­риал на уроке?

Довольно часто если у ребенка нет предрасположенности к счету, то родители и учителя неправомерно связывают это с не­достатком интеллекта, и ставится вопрос о его переводе в специ­альную школу.

Дети группы риска: девочки

В то время как мальчики статистически имеют повышенный риск проявлений трудностей в чтении и правописании, у девочек преобладают арифметические нарушения. Исследование Лобека показало, что из числа всех обследованных детей с арифметичес­кими проблемами примерно 60 % оказались девочки. Однако в со­временных исследованиях указывается на то, что связь между ариф­метическими нарушениями и нейропсихологическими функцио­нальными нарушениями свойственна в большей степени мальчи­кам, чем девочкам. Арифметические трудности у девочек бывают вызваны иными причинами, чем у мальчиков, более всего — пси­хосоциальными. У девочек, как доказано, чаще, чем у мальчиков, развивается страх перед математикой. Кроме того, у них отмечает­ся заниженная самооценка относительно их успехов в счете. Под влиянием негативной самооценки, недоверия к себе и принятых стереотипов («математика — не женское дело») девочки проявля­ют слабую инициативу и, как следствие, имеют меньший успех в области математики. Это позволяет ответить на вопрос, почему в большинстве случаев у девочек не развивается интерес, мотива­ция и готовность к этому предмету.

Дети с арифметическими нарушениями встречаются намного чаще, чем это можно предположить. Лоренц (1993) считает, что примерно 6 % учащихся нужно классифицировать как крайне сла­бых в счете, а примерно 15% учащихся нуждаются в коррекции арифметических нарушений. По мнению Астера, частота неопи­санных случаев математических нарушений у детей так же высо­ка, как в чтении и правописании. Однако надо отметить, что ариф­метические нарушения менее изучены, чем нарушения чтения и правописания.

Базовые составляющие математического мышления (процессы первых ступеней обучения)

Счет — это мыслительный процесс, при котором восприятие, представления, моторика и память теснейшим образом связаны и взаимодействуют друг с другом. Как овладение чтением и пись­мом, так и развитие математического мышления начинается за­долго до поступления ребенка в начальную школу. Зрительно-про­странственные (правое полушарие) и языковые процессы (левое полушарие) обработки информации являются основой для вы­числений. Лурия также указывает на тесную взаимосвязь между счетными операциями, пространственным воображением и от­влеченным (понятийным) мышлением ребенка. Имеется в виду зрительно-пространственная ориентация, образное представление чисел и знание пространственных отношений. Результаты иссле­дования новорожденных показывают, что раннее развитие вни­мания и ощущений ребенка является важной предпосылкой фор­мирования основ познавательной деятельности. Развитие мышле­ния и формирование математических понятий базируются на спо­собности ребенка воспринимать и обрабатывать информацию (т. е. на системе сенсорной интеграции).

Базовыми для обучения математике являются тактильно-кине­стетическое, вестибулярное восприятие, а также зрительное и слуховое.

Маленький ребенок, который хватает предметы и тянет их в рот, с помощью возникающих при этом ощущений определяет их свойства, положение в пространстве и форму. Тактильно-ки­нестетическое восприятие, вступающее в действие, способству­ет также получению опыта о таких свойствах предметов, как «много —мало», «круглый —прямоугольный», «прямо —криво», «жестко — мягко».

У ребенка развивается способность распределять предметы по определенным признакам (например, круглые маленькие дис­ки, четырехугольные маленькие диски). Кинестетическое вос­приятие дает возможность ребенку определить силу своих мышц и расстояние до объекта, что является необходимым условием для развития ориентации в пространстве. В дальнейшем хорошо развитое тактильно-кинестетическое и вестибулярное восприя­тие образует необходимую базу для построения представления о схеме тела, что очень важно для развития способности ориен­тироваться в пространстве, а также для развития зрительного восприятия детей. Благодаря этому дети усваивают такие поня­тия, как «впереди —позади», «наверху—внизу», «справа—сле­ва» и т.д.

Ребенок с хорошо развитой схемой тела имеет возможность определить положение объектов, их пространственные отноше­ния, их порядковые и количественные характеристики.

Упорядочивание предметов по величине и способность к со­ставлению ряда (предметы большие — поменьше — совсем ма­ленькие) представляет собой одну из самых важных основ логи­ческого понимания чисел. Определение положения предмета в пространстве и пространственных отношений представляет собой еще одну функцию, важную для усвоения понятия «количество», а также для формирования представлений о числах.

Хорошо развитая способность ориентации в пространстве так­же имеет важное значение для усвоения системы чисел. Благодаря ей ребенок усваивает такие понятия, как единица, десяток, сот­ня, тысяча и т. п. Порядок чисел в числовом ряду является важ­ным для усвоения счета. Усвоение пространственных отношений — необходимое условие для различения таких цифр и чисел, как 6 и 9, 31 и 13, а также для освоения правильной записи арифмети­ческих действий. При решении уравнений, таких, например, как 25 - 13 = ? или 25 + ? = 28, ребенок должен обладать способностью ориентироваться в пространстве.

На уроке математики в начальной школе можно сразу выде­лить детей с нарушениями пространственной ориентации, так как они, читая или записывая числа, переставляют цифры, например пишут 31 вместо 13. При выполнении заданий на вычитание они меняют направление операции: 12 - 8 = 20. При нарушении про­странственной ориентации у ребенка возникают трудности так­тильно-кинестетического и вестибулярного восприятия. Наруше­ния пространственной ориентации могут возникать в результате торможения доминирующей зоны коры больших полушарий го­ловного мозга. Латеральность у детей с нарушением счета бывает не выражена. Нейропсихологические исследования часто обнаружива­ют у детей с нарушениями счета перекрестную латеральность.

Достаточно хорошо развитая схема тела, а также хорошая ори­ентация в пространстве являются главным условием развития пла­нирования действий. У ребенка создается представление о кон­кретных действиях и способе их выполнения только тогда, когда он что-то делает сам. С возрастом ребенок научается разрабатывать и планировать конкретные действия, необходимые для достиже­ния цели. Если он будет уверенно и четко управлять движениями собственного тела, то ему легче планировать действия и перево­дить движения в представления пространственных отношений. Нарушение схемы тела вызывает недоразвитие схемы действий, тормозит внутренние представления ребенка, без чего невозмож­но выполнение математических операций.

Лоренц (1991) говорит о «визуальном оперировании», т.е. мыс­ленном планировании деятельности. Действия переводятся в представления во внутреннем плане. Ребенок решает, что он должен сделать, чтобы построить определенный объект (например, со­брать машину из деталей конструктора), или сколько кубиков он должен убрать или добавить, чтобы видоизменить предмет. Даже такие ежедневные действия, как намазывание джема на хлеб или доставание мяча из-под шкафа палкой требуют мысленного опе­рирования. Эта способность хорошо проявляется в играх с «лего» и с другими конструкторами. Ребенку, прежде чем начать конст­руировать, нужно представить конструкцию. Мысленное опери­рование развивается у детей на основе самостоятельно выполняе­мых действий и ощущения движений, редко это происходит при наблюдении за действиями, еще реже при рассматривании изоб­ражений.

Вычисление — это чувственное действие. Если действия возни­кают у ребенка в воображении, то он может их запланировать и может мысленно изменить план. Дети, которые испытывают труд­ности при завязывании шнурков на ботинках или в конструктор­ских играх, часто терпят неудачу не столько от того, что их дви­жения неловки, сколько от того, что они не могут запомнить, какие действия необходимо выполнить, чтобы достичь конечного результата. В детском саду эти дети неохотно мастерят, не могут собрать пазлы, «лего» и сконструировать что-либо при помощи фишек даже по образцу.

Даже когда вместо вербальных инструкций детям предлагают пошаговые действия, трудности не уходят. Детям тяжело повто­рить движения, которые они увидели, так как для этого опять-таки необходимо представить действия. Достраивание геометри­ческих форм по памяти (например, в играх со вкладышами) их затрудняет, так как формирование внутреннего плана действий требует стабильной зрительной памяти. Эта способность проявля­ется в таких играх, как «Запомни», «Пазлы», «Дострой ряд из цветных кубиков по памяти» (например, ряд из красных, жел­тых, зеленых, синих кубиков).

В развитии математических понятий важную роль играет функ­ция контроля глазных мышц, которая находится в тесной связи с вестибулярной системой. Недостатки контроля глазных мышц приводят к нарушению координации в системе глаз—рука. Так как при этом нарушении ребенку трудно глазами фиксировать отдельные объекты или отслеживать ряд объектов, то страдают операции сравнения, упорядочивания, а позднее операции сче­та.

Детям также трудно усвоить понятие «количество», что затруд­няет формирование представлений о числе.

Обычно дети в возрасте от 4 до 7 лет отрабатывают принцип счета. Они учат наизусть названия чисел в числовом ряду («один, два, три...») и развивают способность называть количество эле-ментов. Когда при счете они используют слова-числа, они усваи­вают, что имя числительное, например «три», соответствует та­кому же количеству предметов (3 кубика, 3 конфеты). При счете дети, называя числительное, должны пальцами касаться предме­та, например кубика. Для того чтобы ребенок усвоил счет, произ­несение числительного и прикосновение к предмету должны быть синхронны. При этом у ребенка должны быть хорошо развиты координация действий глаза и руки, функция контроля глазных мышц, способность к соблюдению счетного ритма и к концент­рации внимания.

Дети с нарушением восприятия испытывают трудности при ритмическом счете. Если у ребенка нарушена моторика или конт­роль глазных мышц, он не успевает отслеживать перемещение руки при счете, и тогда счет и сопровождающее его движение руки не совпадают. Эти нарушения препятствуют развитию понятия числа у ребенка. Поэтому в дошкольный период необходимо развивать у ребенка технику счета, предлагая для этого счетные палочки, ис­пользуя игры. В дальнейшем, при ослабленном контроле глазных мышц, у детей плохо развиваются навыки чтения, усвоение по­рядка чисел в числовом ряду, им трудно расшифровывать мате­матические формулы.

Все дети еще задолго до поступления в школу могут осуществ­лять некоторые математические операции. Уже в дошкольном воз­расте они могут определить, где «больше» и «меньше» или «очень много», умеют сравнивать множества («меньше чем», «больше чем»), устанавливают отношения величин. Если дети играют с ка­мешками, шариками, кубиками, то они собирают, перекладыва­ют, складывают, нагромождают или откладывают их, осваивая такие понятия, как «много» и «мало», «близко» и «очень далеко», «все» и «ничего». Для развития математического мышления важ­но, чтобы дети имели возможность играть с такими предметами, как кубики, шарики, палочки, конструкторы, и манипулировать ими. Укладывая кубики в ящик, они считают: «Один, два, три...». Сначала, определяя количество предметов, они загибают паль­цы, а позднее следят только глазами. Оперируя игровым материа­лом, дети осваивают принципы сложения и вычитания (кубиков стало больше или меньше), а также принцип перехода от частей к целому. Благодаря зрительному и тактильно-кинестетическому опыту, накопленному в игре с предметами, дети усваивают поня­тие числа. Со временем, уже не нуждаясь в непосредственном на­блюдении за предметами, они понимают, что значит структура и порядок чисел (Пиаже, 1965). Если даже они не видят предметы и не касаются их, они могут сказать, например, что 7 яблок боль­ше, чем 5.

Исследование Шмидта (1982) показало, что почти все дети умели обращаться с числами еще до поступления в школу. Почти все учащиеся I класса могли считать. Способность к вербальному счету до 10 была выявлена у 96 % учащихся I класса, 70 % из них могли считать до 20. Примерно 90 % детей могли соотнести числи­тельное «пять» и примерно 78 % числительное «шесть» с соответ­ствующим количеством предметов.

Наряду со способностью определять положение в пространстве у ребенка должна развиваться способность различать основные формы, вести прямой и обратный счет, а также делить числа. На­рушения восприятия формы могут привести к нарушениям понимания последовательности чисел, а это затрудняет форми­рование количественных представлений и выполнение графичес­ких заданий.

Постоянство зрительного восприятия предполагает способность ребенка узнавать знакомые объекты, например, геометрические фигуры независимо от их расположения в пространстве, цвета и размера. Расстройство этой функции восприятия приводит к ухуд­шению способности ребенка определять признаки предметов и вместе с тем к нарушению формирования логического мышления. Детям трудно, например, среди других фигур найти все треуголь­ники.

Уже в дошкольном возрасте у детей происходит развитие зву­кового образа слова, имеющее важное значение для усвоения чи­сел, количественных представлений и вычислительных операций. При поступлении ребенка в школу большое значение имеет спо­собность правильно воспринимать слова на слух. Дети должны уметь слышать голос учителя на шумовом фоне.

Дисфункция основных форм восприятия приводит к тому, что дети переводят свое внимание на самый сильный звуковой сиг­нал (например, топание ног). Дети не могут концентрироваться на важном в данный момент сигнале — на голосе учителя или ответе одноклассника — и выделять их из сильного шумового потока в классе. Эти ученики с большим трудом воспринимают содержание урока. Он «проходит мимо ушей», что приводит к большим пробелам в учебе. Причем дети могут иметь сосредото­ченное выражение лица, но это не значит, что они слышат учи­теля.

Большое значение имеет фонематический слух — способность к различению звуков в слове.

Чтобы формировались правильные понятия, в частности ко­личественные представления, дети должны уметь отличать сходно звучащие слова, такие, например, как «восемь» — «семь», «де­сять» — «девять», т.е. должны воспринимать на слух и различать фонемы (звуки).

Неспособность к различению звуков препятствует формирова­нию ясных представлений о числах и особо сказывается при овла­дении устным счетом.

Лекция 7. Процессы памяти

В последние годы проводится много исследований, посвящен­ных изучению процессов памяти. Литература на эту тему обшир­на, однако мы сможем рассмотреть только некоторые из основ­ных аспектов проблемы.

Традиционно выделяется несколько видов памяти в зависимо­сти от продолжительности ее функционирования.

Ультракороткая память (УКП). Время действия ее длится прибли­зительно от 200 до 300 мс, она располагает огромными возможностя­ми для записи информации. Можно предположить, что УКП через смысловые каналы схватывает всю поступающую информацию. Од­нако из всего объема отбирается только то ее количество, которое в дальнейшем будет кодироваться, сохраняться и передаваться в крат­ковременную память.

Кратковременная память (КВП). Продолжительность ее действия составляет приблизительно 20 с. На этой фазе происходит переработ­ка информации, переходящей в долговременную память. Этому мо­гут помешать отклонения в функционировании таких важных струк­тур головного мозга, какой является гипокампус (структура лимбической системы).

В отличие от ультракороткой памяти объем кратковременной памяти ограничен. В КВП могут сохраняться до 7 (плюс-минус 2) информационных единиц.

Детям дошкольного возраста для запоминания требуется го­раздо большее время, чем это указано выше. Если дети использу­ют разнообразные стратегии запоминания, то за период от ран­него детства до подросткового возраста это время сокращается. Благодаря активизации электрических импульсов обработка и со­хранение информации в памяти осуществляются более успешно. Лишь только та информация, которая активно обрабатывается в течение 30 с, переходит в долговременную память и там сохраня­ется. Путем кратковременного запоминания обрабатываются, на­пример, многоэлементные устные задания.

Долговременная память (ДВП). Долгосрочное хранение информа­ции связано с биохимическими процессами, например с образова­нием рибонуклеиновых кислот и управляющих поведением пепцидов. Структуры лимбической системы принимают активное участие в пе­реносе новой информации в долговременную память. ДВП не пред­ставляет собой единого целого, а состоит из многочисленных компо­нентов:

а) память для фактов и событий. Запоминается информация, ко­торая приобретается путем личного опыта, основывается на знании языка, правил, концепций, например знания о том, как проводятся вычислительные операции (собственно вычислительные шаги, стра­тегии);

б) память, в которой происходят бессознательные процессы па­мяти (не декларативная память). В ней формируется содержание для когнитивных и двигательных навыков (Оертер и Монтада, 1995; Бад-делей, 1986; Рахманн, 1988).

Результаты выполнения заданий (например, разовых заданий) переносятся из ДВП в оперативную память, и таким путем фор­мируются знания о способе выполнения действий для каждо­го вычислительного действия. Ребенок планирует способ действия и группирует отдельные вычислительные шаги в осмысленную последовательность.

В последних исследованиях, посвященных памяти, выражается мнение, что существуют многочисленные модели сохранения информации.

Брайнерд (1985) говорит о различных специализированных функциях памяти. Память представляет собой непрерывное дей­ствие различных структур запоминания информации, которые на одном конце перерабатывают воспринятую информацию с деталь­ной точностью (например, ребенок произносит числовой ряд), а на другом — выполняется переработка этой информации, содер­жащей уже только основной ее смысл, значимый для дальнейше­го ее сохранения в памяти (например, удержание в памяти вы­числительных стратегий).

Гатеркол и Бадделей в своей модели словесной памяти выде­ляют две различные подсистемы:

• артикуляторную, или фонологическую, которая отвечает за пе­реработку языковой информации;

• зрительно-пространственную, которая обрабатывает образную информацию и представления.

Обе подсистемы функционируют независимо друг от друга. Ра­бочая (оперативная) память удерживает информацию и пошаго­вый план для непосредственных действий, например, сохраняет числа, промежуточные результаты и необходимые вычислитель­ные операции. Рабочая память служит для планирования процесса и контроля над правильным ходом арифметических вычислений. Например, при решении устной задачи: 48 - 25 = ? ребенок дол­жен опираться на свою память и использовать арифметические стратегии, которые уже содержатся в его оперативной памяти:

1. он должен узнать числа;

2. знак «минус» означает, что число станет меньше;

3. десятки и единицы будут вычитаться, т. е. надо совершить два действия;

4. сначала отнять десятки от десятков (получится 20), запомнить промежуточный результат, а потом отнять от единиц единицы (полу­чится 3).

Для решения этой задачи, которое требует последовательно­сти действий, ребенок должен обладать хорошей рабочей (опера­тивной) памятью и концентрацией внимания.

Новые исследования показывают что память не является еди­ной цельной функциональной структурой. Например, у ребенка могут быть средние показатели слуховой памяти и достаточно высокие — зрительной. Деятельность памяти по-разному проявля­ется в зависимости от содержания задания (оно может быть слухо-речевым, зрительнообразным, тактильно-кинестетическим) и установки (например, узнавание, воспроизведение и т.д.).

Последние исследования свидетельствуют о том, что между успешностью в деятельности запоминания и отдельными функ­циями памяти существуют слабо заметные взаимосвязи.

Имеются доказательства, что между прочностью памяти и спо­собностью быстрого извлечения информации из памяти (на­пример, быстрое припоминание слов или понятий) существует тесная взаимосвязь. Продуктивность памяти в высокой степени зависит от эмоционального состояния и от мотивационных усло­вий. Страхи, эмоциональные проблемы и усталость оказывают отрицательное влияние на продуктивность памяти. Сниженное внимание, низкая инициатива, нарушенная концентрация внимания, отсутствие интереса оказывают сильное влияние на про­дуктивность памяти.

Страх перед учебой и общением, что особенно свойственно отстающим учащимся, блокирует большую часть рабочей (опера­тивной) памяти и уменьшает объем запоминания, а это приводит к более длительному процессу обучения вычислительным опера­циям.

В последнее время высказывается мнение о том, что наруше­ния функций эндокринных желез (например, щитовидной желе­зы) могут негативно влиять на деятельность памяти.

Детям с нарушениями процесса памяти необходимо предла­гать такую форму подачи материала, которая будет вызывать у них интерес. Эмоциональные установки в обучении оказывают поло­жительное влияние на продуктивность памяти и усвоение мате­риала. Память, внимание, аффект и эмоции развиваются в тесной взаимосвязи.

Снижение функций памяти

У детей с математическими нарушениями наблюдается сниже­ние функций памяти. Объем сохранения информации при слухо­вом восприятии у них недостаточен, что приводит к трудностям ее последовательной переработки, т. е. переработки тех сигналов, которые поступают последовательно друг за другом в память ребенка (например при пошаговых подсчетах или решении по це­почке), что затрудняет «оседание» информации в долговремен­ной памяти.

Снижение функций слуховой памяти проявляется:

• при восприятии звукового ряда. Дети нечетко воспринимают слова, особенно трудны для них сложные составные числа, та­кие, например, как «сто шестьдесят пять»;

• при восприятии на слух текста — целого ряда слов или пред­ложений. Чтобы запомнить задание или объяснение учителя, ре­бенок должен владеть кратковременным запоминанием услышан­ного. При нарушении этой способности он не может понять смысл текстовых заданий;

• при устном счете. Так, например, при устном решении зада­чи 63 - 25 = мысленно следует совершить несколько операций. Сначала оба числа нужно сохранить в кратковременной памяти, потом число 25 нужно разделить на десятки и единицы и тоже сохранить полученные результаты вычислений в кратковремен­ной памяти, потом нужно 20 вычесть из 63 и запомнить промежу­точный результат (43) и затем из этого числа вычесть 5. Все эти вычисления возможны при условии хорошо функционирующей кратковременной памяти, сохраняющей все нужные числа и про­межуточные результаты. Ребенок должен понимать алгоритм вы­читания, то, каким образом ему следует выполнять задание, т.е. он должен активизировать в памяти весь ход вычисления. Наруше­ние внимания и его концентрации ухудшает запоминание чисел и промежуточных результатов;

• в трудностях при изучении таблицы умножения. Нарушение способности запоминать связано с тем, что у ребенка ослаблен процесс долгосрочной автоматизации порядка таблицы и ребе­нок быстро ее забывает. При слабой автоматизации таблицы ум­ножения детям приходится кропотливо высчитывать результаты, что приводит к перегрузке объема кратковременной памяти. Дети забывают промежуточные результаты и снова и снова повторяют весь процесс подсчета. Затрудняется и автоматизация определен­ных типов заданий, таких как усвоение порядкового счета, на­пример счета до 20. Преимущество автоматизации состоит в том, что сокращается время на решение задания, в результате чего про­исходит разгрузка оперативной памяти;

- в трудностях классификации. Дети теряются, если получают задание, содержащее сразу несколько требований, например, если надо классифицировать карточки, руководствуясь не одним, а не­сколькими признаками: признаком цвета (красные), размера (ма­ленькие) и формы (треугольные). При нарушении внимания дети не могут сразу переработать сложные указания к действию и запо­минают только первые и последние информативные блоки рече­вого потока. Детям с нарушением сохранения информации трудно удержать в памяти новые названия и определение математи­ческих понятий (на уроке математики в начальной школе вводят­ся до 500 новых понятий);

- в трудностях соединения известного и неизвестного. Так как у детей ограничен объем памяти, то они не могут соотнести но­вую информацию с уже выученным материалом и оценить ее значение. Накопленные блоки в памяти не связываются друг с другом. Это приводит к нарушениям в развитии вычислительных действий (например, в заданиях, где требуется поменять числа местами);

• в трудностях формирования представлений о числах и вос­произведения отношений между числами. Дети не могут вы­строить ассоциативные связи между цифрами и их наименова­ниями, так как забывают, что слово «пять» соотносится с циф­рой «5»;

• в нарушении сохранения в памяти информационных бло­ков (памяти на последовательность чисел и звуков). Дети с тру­дом усваивают числовой ряд (1, 2, 3, 4, 5). Обычно ребенок, помня наизусть числовой ряд, может выделить число и связать с ним соответствующее количество элементов, может для каждого числа подобрать соответствующее слово-цифру: «пять, шесть». На­рушение блоков памяти затрудняет усвоение и воспроизведе­ние элементов определенного ряда и затрудняет ориентацию в числах.

Штранг и Рурке (1985) выделяют 2 группы детей с нарушени­ями счета:

- у детей одновременно плохо развиты способности в счете, чте­нии и правописании. По мнению авторов, проблемы в обучении этих детей заключаются в нарушении слухового внимания, т. е. у детей плохо развита слуховая различительная способность при кратковременном запоминании;

- у детей плохо развита способность к счету вследствие наруше­ний в области зрительно-пространственного и телесного восприятия (нарушение схемы тела). Эти дети испытывают трудности в усвоении чисел, в понимании пространственного соотношения чисел и соот­ветствующего алгоритма решения.

Следующим видом памяти выступает стабильная зрительно-пространственная память, выполняющая важную роль в развитии математического мышления. У детей с нарушениями счета возни­кают трудности в сохранении и воспроизведении информации, связанной со зрительно воспринимаемыми геометрическими об­разами. В дошкольном возрасте обычно эти способности проявля­ются у детей в таких играх, как «Память», «Пазлы», «Постройки из кубиков» или «Изображение геометрических фигур по памяти». Астером (1992) было проведено исследование, выявившее, что у детей с нарушениями счета особые трудности вызвали задания, в которых требовалось запомнить, а затем по памяти воспроизвести представленные для зрительного восприятия геометрические фи­гуры.

Речевая память и понимание речи должны рассматриваться как основа развития математических способностей. Речь и мы­шление, речь, математическое знание и планомерная деятель­ность находятся в тесной взаимосвязи. Ограниченная возмож­ность некоторых детей воспринимать речь, понимать и исполь­зовать ее влияет на формирование математических способно­стей.

Речь — важнейшее средство для закрепления, обработки и воспроизведения содержания памяти. Недостаточное владение речью может привести к нарушению процессов запоминания и сохранения в памяти определенного содержания. И, наоборот, плохо функционирующая память может вызвать речевые нару­шения.

Проговаривание содержания предмета способствует его пони­манию и запоминанию. Учащиеся воспринимают содержание ма­териала, вырабатывают план решения, обсуждают его с однокласс­никами, выстраивая с помощью речи деловые отношения на уро­ке. Они сообщают свои соображения, предлагают варианты дей­ствия, намечают цели, запоминают и в нужный момент воспро­изводят.

Речь выступает средством самоконтроля (например, внутрен­няя речь) и средством поддержания и концентрации внимания. Дети с речевыми нарушениями или с ограниченным словарным запасом воспринимают речь фрагментарно и смысл сказанного от них ускользает.

Они плохо понимают отношения, содержащиеся в заданиях, например:

• обстоятельственные (где: «на — под — рядом — перед — между»);

• компаративные (сравнения) («больше чем — меньше чем»);

• количественные («один — много»);

• причинно-следственные («потому что», «так как»).

Дети испытывают трудности, когда, читая задания к тексту, они не могут его осмыслить или когда встречают в тексте незна­комые слова.

Трудности в обучении математике могут возникать и потому, что на уроке используются понятия, которые недоступны детям, такие, например, как «еженедельно», «введение — заключение — вывод». В этом случае непонимание бывает вызвано не трудностью освоения математических действий, а сложностью речи учителя, содержащей незнакомые детям термины.

Лекция 8. Функции, развитие которых необходимо для овладения понятием числа

Как было уже сказано, развитие математического мышления в большой степени зависит от освоения ребенком системы зритель­но-пространственных отношений, что происходит благодаря его действиям с разными предметами. Над проблемой развития поня­тия о числе много работал Пиаже (1965). Математическое мышле­ние — это пространственное мышление. Для усвоения четырех основных видов математических действий — сложения, вычита­ния, умножения и деления — у ребенка должны быть хорошо развиты пространственное представление и мышление. Мы гово­рим о пространстве чисел («10», «20»), о расширении вычисли­тельного пространства. Мы измеряем длину, протяженность, рас­кладываем числа, составляем частичные множества. При этом всегда речь идет об отношениях в пространстве. Пространственное мышление и оперирование им выступают предпосылкой для по­нимания математических операций. Понимание действий с чис­лами зависит в первую очередь от развития трех функций:

• способности классифицировать (классификация);

• способности построения ряда (сериация);

• способности находить соответствия 1:1.

Чтобы классифицировать предметы, ребенок должен уметь вы­являть их сходство и различие и соответственно их группировать. Важной предпосылкой для этого является образование таких по­нятий, как «все красные треугольники». Осознание схожести пред­метов позволяет детям развивать понятия «такой же», «такие же», символизируемые значком =, смысл которого становится теперь ребенку понятен.

Чтобы построить ряд (серию) (рис. 19), ребенок должен владеть способностью подобрать предметы и соотнести их по убывающе­му (возрастающему) признаку (например, разложить в опреде­ленной последовательности предметы, разные по длине). Выпол­нение этих заданий возможно в том случае, если у ребенка хоро­шо развита ориентация в пространстве. Упражнения в составле­нии ряда предметов учат понимать число как выражение величи­ны и порядка. Если ребенок не может построить ряд предметов, то это значит, что у него нарушены вычислительные операции.

Способность устанавливать взаимнооднозначное соответствие является важной предпосылкой для того, чтобы ребенок мог ос­воить понятие «много одинаковых». Выполняя такие задания, ре­бенок учится шаг за шагом узнавать отношения «много одинако­вых — не все одинаковые — меньше, чем — больше, чем». Спо­собность понимать соотношение 1: 1 развивается в возрасте от 4 до 7 лет. Она тесно связана с усвоением количественных значений. При выполнении таких заданий ребенок начинает понимать, что такое вариативность. Благодаря таким действиям, как «дополнить», «доложить», «достроить», у ребенка развивается понимание мате­матических операций сложения или вычитания и формируется представление о величине, связанное с числами.

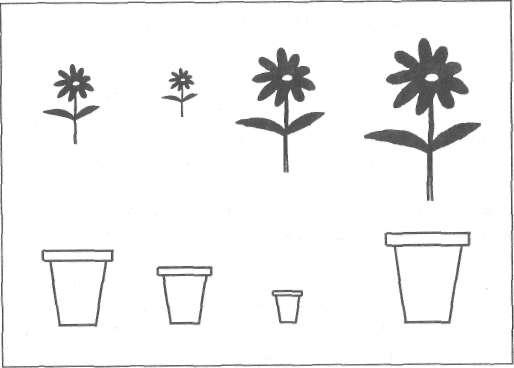
Рис. 19. Построение ряда: какой цветок подходит для какого горшка?

Наиболее часто встречающиеся затруднения в вычислениях

Лобек провел среди учителей опрос по поводу наблюдающих­ся у детей нарушений механизмов вычисления. Ему удалось уста­новить, что чаще всего встречаются следующие трудности в осу­ществлении вычислительных операций:

• затруднения в выборе вычислительной стратегии, если имеет место отступление от усвоенного способа действий. Если при реше­нии задания 3 + 8=11 ребенок не испытывает трудности, то решение равенства, где не хватает одного члена, (... +5 = 8), дается намного труднее. Чтобы выполнить подобное задание, дети должны понять взаимообратимость действий сложения и вычитания;

• дети переставляют цифры при прочтении и написании чисел: 17 + 4 = 12 (вместо 21), 7 + 8 = 51 (вместо 15);

• дети не видят разницы в том, какую позицию занимает цифра в системе числа. Числа 23 и 32, 104 и 401 они считают одинаковыми;

• их затрудняет чтение символов «+» и «-», они их путают;

• испытывают трудности в понимании таких величин, как время и деньги. Здесь, прежде всего, у детей возникают трудности в называ­нии именованных чисел и операциях с ними.

Влияние математических нарушений на самооценку, личностное и эмоциональное развитие ребенка

Нарушения в счете могут привести к многочисленным расстрой­ствам в развитии ребенка. Это может быть:

- заниженная самооценка («я глупый»). Такие дети не уверены в себе;

• моторное беспокойство;

• плохая концентрация, высокая отвлекаемость;

• позиция аутсайдера;

• отказ от деятельности, вызванный страхом перед результатом, перед школой, боязнью потерпеть неудачу;

• отсутствие усидчивости, быстрая утомляемость;

• многочасовая подготовка домашних заданий, которые выполня­ются очень медленно и обстоятельно, особенно при счете;

• усиленный поиск помощи, просьбы о ней или, напротив, пол­ный отказ от нее;

• быстрая, лихорадочная, поверхностная работа с целью скорей­шего освобождения от нее;

• угадывание ответов при решении;

• умолчание о том, что задано домашнее задание;

• упадок настроения при неудаче;

• проявление приступов ярости и агрессии, если вычисления не получаются.

Лекция 9. Области диагностики для детей дошкольного возраста при поступлении в школу или в начале обучения

Процесс обучения математике требует достаточного уровня способностей ребенка:

• моторных;

• тактильно-кинестетического и вестибулярного восприятия;

• способности ориентироваться в пространстве, осознания схемы своего тела и планирования действий;

• зрительного восприятия;

• слухового восприятия;

• сенсорной интеграции различных областей восприятия;

• зрительного и слухового запоминания, памяти;

• вербальной памяти и понимания речи.

Функциональные расстройства в области слухо-речевого и те­лесно-пространственного восприятия приводят к нарушениям процессов математического мышления. Это учитывают, обследуя развитие ребенка в раннем возрасте. В это время возможно вы­явить имеющиеся отклонения и разработать соответствующие ме­роприятия. Чем раньше это будет сделано, тем больше вероят­ность успеха.

Обобщая опыт нейропсихологической диагностики матема­тических нарушений у детей дошкольного и младшего школьно­го возраста, можно выделить следующие особенности обследуе­мых:

• у детей нарушено тактильно-кинестетическое восприятие. Так, они плохо определяют место раздражения при прикосновении. Если прикоснуться к пальцу ребенка, в то время как у него закрыты глаза, то просьба показать соответствующий палец на другой руке его затруднит: это так называемая агнозия пальцев. Страдает стереогностическое восприятие: ребенок не может опознать предмет путем его ощупывания;

• отсутствует ориентация в собственном теле. Представление о схеме тела не сформировано у ребенка в соответствии с его возра­стом;

• дети плохо ориентируются в пространстве, с трудом осваи­вают понятия «впереди», «сзади», «наверху», «внизу», «рядом», «справа», «слева». Недостаточно сформированы пространственно-временные представления, представления о величине и расстоя­нии. Ребенку трудно определить, сколько шагов отделяет его от двери, сравнить предметы по величине и т.д.;

• детям трудно дается систематизация — упорядочивание пред­метов по заданным признакам (например, надо выделить все го­лубые четырехугольные пластинки);

• дети сталкиваются со значительными трудностями при пла­нировании действий. Им не интересны игры в конструктор, так как у них нет четкого представления о порядке действий (шагах), а такие представления необходимы при конструировании. Они из­бегают игр, требующих запоминания, неохотно берутся за пазлы, конструктор «Лего», кубики;

• дети испытывают особые трудности при воспроизведении дви­жений, поскольку для этого надо не только уверенно владеть соб­ственной моторикой, но и мысленно представлять процесс дви­жения, т.е. планировать его ход;

• у детей могут возникать трудности при определении порции еды, которую надо положить на тарелку или взять ложкой. Им сложно в правильной последовательности надевать на себя пред­меты одежды;

• они не умеют двигаться спиной вперед или пятиться назад, так как не ориентируются в пространстве;

- латеральность у этих детей не сформирована. Дети не умеют выполнять перекрестные действия, например, левой рукой до­тронуться до правого уха;

• плохо развита как крупная моторика (это проявляется во время бега, в позе стоя на одной ноге, при ходьбе по одной линии), так и мелкая (проявляется во время завязывания шнурков на ботин­ках, застегивания пуговиц на куртке, дорисовывания картинки), так как у них нарушены координация в системе глаз — рука и зри­тельно-мышечный контроль;

• с трудом осознается соотношение предметов по величине: не удается составление ряда, например распределение карандашей по длине;

• дети не могут на взгляд определить количество представлен­ных им предметов. Если группа состоит из 5 —6 элементов, они пересчитывают их по пальцам. Им трудно бывает сказать, какая группа предметов содержит больше элементов, например, где лежит больше палочек;

• они не могут припомнить и назвать 3 — 5 предметов (это мо­жет быть расческа, ключ, ластик и карандаш), показанных им, а затем спрятанных под платком;

• им трудно воспроизвести по памяти очередность, в которой были показаны 3 — 4 разноцветные деревянные палочки (напри­мер, желтая, красная, зеленая, голубая);

• трудности возникают, если из деревянных палочек надо вос­произвести простую геометрическую форму, например звезду или стул;

• при нарушении слуховой памяти детям не удается повторить за говорящим ряд чисел из 4 —5 элементов или ряд слогов (на­пример, «по-ко-то-ви»). Им трудно выучить наизусть стихи;

• дети с трудом овладевают такими понятиями, как «больше —меньше — столько же» (количество); «меньше чем — больше чем» (размер);

• любой пересказ вызывает затруднения, даже если это пере­сказ маленькой истории. Дети затрудняются в достоверной пере­даче пространственных и временных отношений;

• возникают трудности при выполнении поручения, если оно требует совершения нескольких (2 — 3) действий, (например: «Возьми с полки маленький голубой кубик и положи на стол около желтого кубика»);

• дети не могут хлопками в ладоши воспроизвести ритм, со­стоящий из 4—5 ударов;

• дотрагиваясь рукой до предмета при счете, дети сбиваются с ритма: счет и движение не совпадают;

• наблюдаются трудности в понимании некоторых количественных числительных: дети не соотносят их с реальным числом предметов;

• к концу пребывания в детском саду у них еще не сформиро­вались количественные понятия «5» и «6»;

• вызывает трудности осознание порядковых числительных, обо­значающих место элемента внутри ряда. Это выявляется следующим образом. Перед ребенком выкладывают ряд деревянных палочек, и взрослый, прикасаясь к первой палочке, говорит: «Это первая па­лочка, покажи мне шестую, третью, предпоследнюю палочку»;

• дети плохо различают звуки, соответственно, затруднено раз­личение числительных (например, 31 и 13);

• дети не могут воспроизвести соотношение 1:1. Это проявля­ется, например, в том случае, если ребенку надо решить, сколь­ко еще тарелок надо поставить на стол, чтобы смогли поесть шесть человек.

Как при нарушениях в чтении и правописании, так и при ма­тематических нарушениях описанные выше симптомы могут выс­тупать в различных проявлениях и комбинациях.