Тема 6. Исследование функций двух переменных

6.1. Типовые примеры

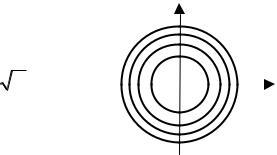
Пример 6.1.1. Построить линии уровня функции z = x2 + y2 .

Решение.

Уравнение

линии

уровня

y

z =C x2 + y2 =C является уравнением окружности с

центром в начале координат и радиусом R =

C .

0

1 2 x

Если придать постоянной C значения 1, 2, 3,..., то полу-

чим

семейство

концентрических

окружностей

(рис.12.5). Расстояние между линиями уменьшается при

РИС. 6.1.1

увеличении C .

Пример 6.1.2. Найти

частные

производные

∂z ,

∂z

функции

∂x

∂y

z = xln y + x2 − 2 y + xy и найти ее частные значения в точке M (1,1).

Решение. Последовательно получаем:

∂z = ln y + 2x + y,

∂z

=

x

− 2 + x ,

∂y

y

∂x

∂z

x=1 = ln1 + 2 +1 =3,

∂z

x=1 =1 − 2 +1 = 0 .

∂x

y=1

∂y

y=1

Пример 6.1.3. Найти полное приращение

z и полный дифференциал dz

функции z = x2 + xy и вычислить их при x =1,

y =1,

x = 0,1,

y = 0,2

0

0

Решение. Найдем полное приращение функции

z = f (x + x, y + y)− f (x, y)=

=(x + x2 )+ (x + x)(y + y)− x2 − xy =

= x2 + 2x x + (

x)2 + xy + x y + y x + x

y − x2 − xy =

= (2x + y) x + x y + ( x)2 + x

y .

Вычислим z при x0 =1, y0 =1,

x = 0,1,

y = 0,2 :

(

z)0 = 3 0,1 + 0, 2 + (0,1)2 + 0,1 0, 2 = 0,53.

Найдем частные производные

29

∂z = 2x + y,

∂z

= x

и запишем дифференциал

∂x

∂y

dz =(2x + y) x + x y

Подставим в dz значения x0 ,

y0 ,

x,

y , получим

(dz)0 =3 0,1 +1 0, 2 = 0,5 .

Убеждаемся в приближенном равенстве dz ≈

z.

′′

′′

′′

функции

Пример 6.1.4. Найти производные zxx ,

zxy , zyy

z = 2x3 −3y2 + xy +1.

Решение. Найдем производные первого порядка

′

= 6x

2

′

= −6 y + x .

zx

+ y, zy

Дифференцируя эти производные, получаем:

′′

′ ′

′′

′ ′

′′

′ ′

= −6 .

zxx =(zx )

x

=12x, zxy

= (zx )

y

=1, zyy

= (zy )

y

ке P

∂u

= 2 y2 + 2,

∂u

(P)= 4,

∂x

∂x

∂u

= 4x y − z + 2 y,

∂u

(P)= −8,

∂y

∂y

∂u

= −y − 2z,

∂u

= −3.

∂z

∂z

G

G

Найдем направляющие косинусы вектора

= 9 + 0 +16 = 5 ,

A. Так как

A

то cos α =

3

, cosβ = 0, cos γ = − 4 .

5

5

ке P

∂u

= 2x −3z,

∂u

=

4 y,

∂u

= −3x + 2z,

∂x

∂y

∂z

∂u

(P)=5,

∂u

(P)=8,

∂u

(P)= −5.

∂x

G

dy

G

∂z

G

Составим вектор grad u =5i +

8 j − 5k , тогда

max ∂u =

gradu

=

25 + 64 + 25 = 114 ≈10.68 .

∂A

Пример 6.1.7. Найти экстремумы функции

z = x3 + y3 − 3xy .

Решение.

1) найдем частные производные

∂z

=3x2

−3y,

∂z = 3y2 − 3x .

∂x

∂y

Составим и решим систему уравнений

∂z

= 0

∂x

2

− y

= 0

= x

2

x

y

∂z

2 − x = 0

− x =

= 0

y

x4

0

∂y

2

y = x

P

(0, 0), P (1,1) –

x(x3 −1)

= 0

1

2

критические точки;

2) найдем вторые частные производные

∂2 z

= 6x,

∂2 z

= 6 y,

∂2 z

= −3

∂x2

∂y2

∂x ∂y

Найдем значения

в критических точках:

(P1 )= −9 < 0 P1 не является точкой экстремума,

(P )= 27 > 0 P

– точка экстремума. Так как

∂2 z

(P )= 6

> 0 , то

P –

2

2

∂x2

2

2

а) z = y − x

2

; ;

б) z =

x2

y2

в) z =

y

; ;

г) z = y − e

x

..

+

; ;

x2

9

4

32

а)

∂3 z

=? z = 4xy3

− 2x2

+ 3y −1;

∂x∂y2

б) z(42 )2 =? z =3x2 y2

− 2 y3

+ x2 ;

x y

в)

∂5 z

=? z = x4 y3 .

∂x2∂y3

Найти производную по направлению

∂u

в точке P в направлении A:

G

∂A

6.3.8.

u = x2 + y2 + z2 , P(1,1,1),

A = (cos 45°, cos60°, cos60°);

6.3.9.

u = y3 − x2 + 2x y z, P(1,1, − 3),

G

A – луч, составляющий с осями коорди-

нат Ox, Oy, Oz углы 90°, 60°, 30°;

6.3.10.

u =3x2 − 5y + 2z2 ,

G

= (1, −1, 0);

P(1, 0,1), A

6.3.11.

u = 2x2 −3y + 4z + x2 y2 z2

, P(1, 0, 2),

G

A = (1, −1, 2);

6.3.12.

u = 2x y − x2 + y2 + 2z, P(0,1, −1),

G

JJG

A = OP ;

6.3.13. Найти max ∂u (наибольшее значение производной) данной функции в

∂A

заданной точке:

а) u = x2 + y2 + z2 − x y +1, P(2, 0, − 2);

б) u = x y + y z2 − 2x + 2 y − z, P(1, − 2, −1);

в) u = x2 y + 3y2 − 2z +1, P(−1, 1, 1).

Найти экстремумы функции:

6.3.14.

z = 2x2 + y2 + 5;

6.3.15.

z = 2x y − 4x − 2 y ;

6.3.16.

z = x2 − x y + y2 − x + 3 ;

6.3.17.

z = 2x3 − x y2 + 5x2 + y2 ;

6.3.18.

z = x + y − x2 − x y − y2 + 2 ;

6.3.19.

z =3x + 6 y − x2 − x y − y2 .

3

34